MATLAB The Workspace Browser MATLAB The Array Editor

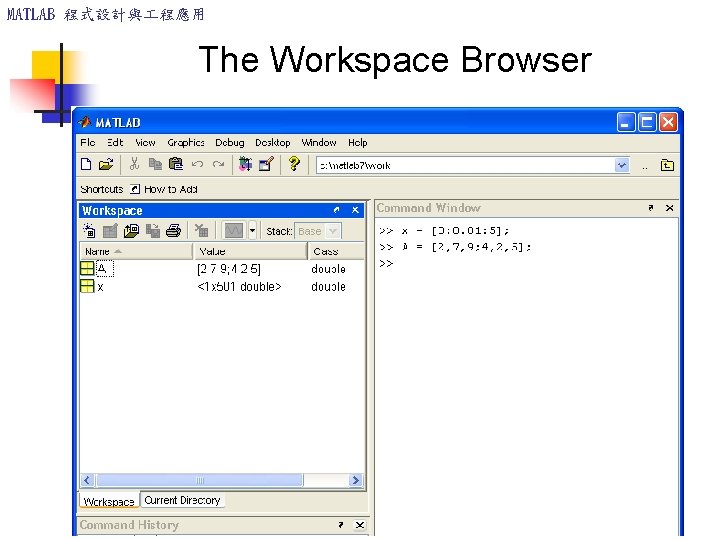
MATLAB 程式設計與 程應用 The Workspace Browser

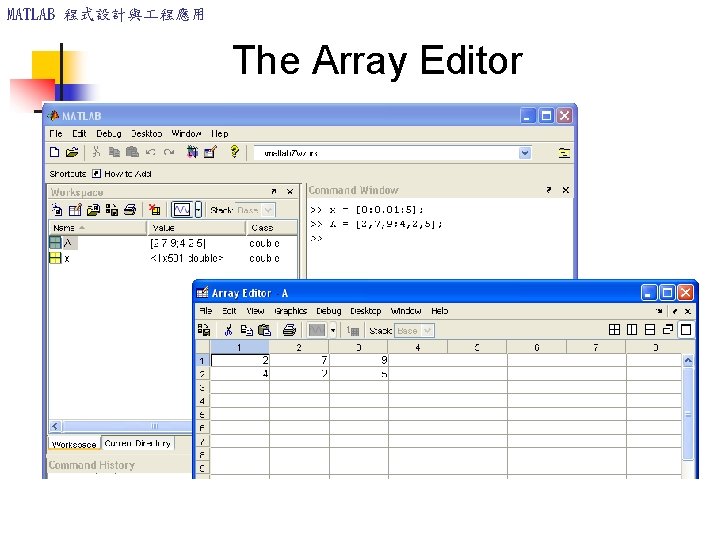
MATLAB 程式設計與 程應用 The Array Editor

MATLAB 程式設計與 程應用 n n n >>tic; >>for i=1: 1: 10000 >>disp i >>end >>tac;

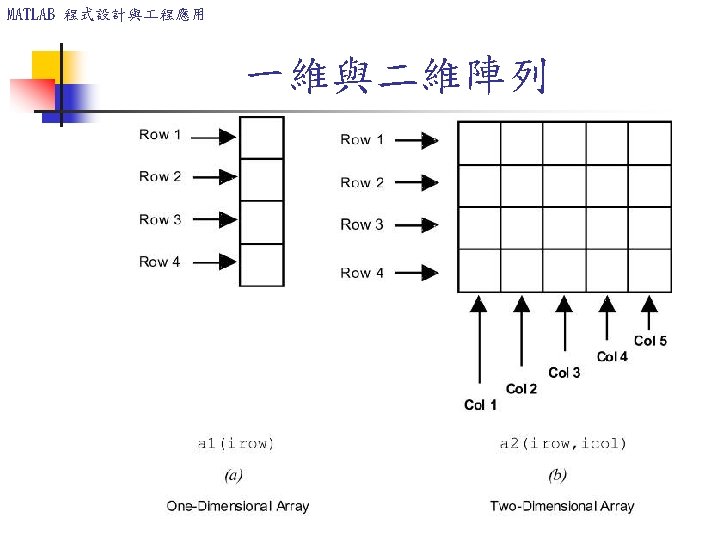
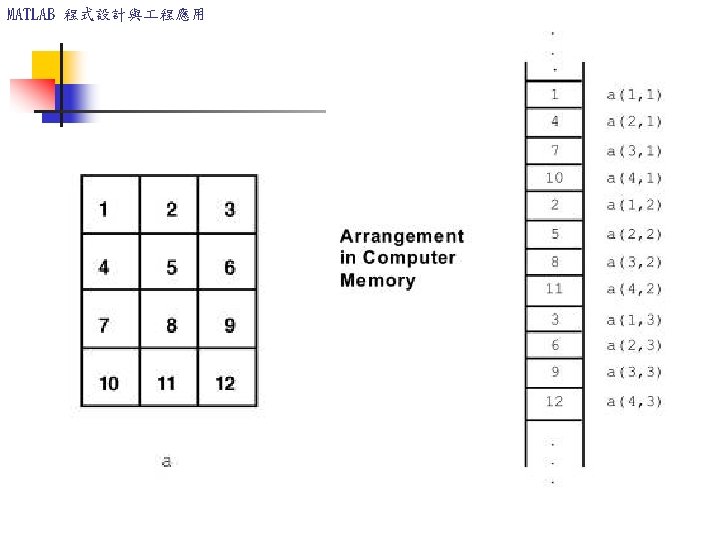
MATLAB 程式設計與 程應用 Multidimensional Arrays Consist of two-dimensional matrices “layered” to produce a third dimension. Each “layer” is called a page. cat(n, A, B, C, . . . ) Creates a new array by concatenating the arrays A, B, C, and so on along the dimension n.

MATLAB 程式設計與 程應用 矩陣與向量 A matrix has multiple rows and columns. For example, the matrix 2 4 10 M = 16 3 7 8 4 9 3 12 15 has four rows and three columns. Vectors are special cases of matrices having one row or one column.

MATLAB 程式設計與 程應用 To create a row vector separate the elements by semicolons. >>p = [3, 7, 9] p = 3 7 9 create a column vector by using the transpose notation (‘). 轉置矩陣 >>p = [3, 7, 9]' p= 3 7 9

MATLAB 程式設計與 程應用 Create a column vector You can also create a column vector by separating the elements by semicolons. For example, >>g = [3; 7; 9] g = 3 7 9 比較轉置矩陣與 ROT 90 函數的差別 >>p = [3, 7, 9]' p= 3 7 9

MATLAB 程式設計與 程應用 Create vectors by ''appending'' one vector to another. r = [2, 4, 20]; w = [9, 6, 3]; >>u = [r, w] u= >>u = [r ; w] u= [ 2, 4, 20, 9, -6, 3]. [ 2 4 20 9 -6 3 ].

MATLAB 程式設計與 程應用 generates a large vector The colon operator (: ) easily generates a large vector of regularly spaced elements. Typing >>x = [m: q: n] creates a vector x of values with a spacing q. The first value is m. The last value is n if m n is an integer multiple of q. If not, the last value is less than n.

MATLAB 程式設計與 程應用 For example, typing x = [0: 2: 8] creates the vector x = [0, 2, 4, 6, 8], whereas typing x = [0: 2: 7] creates the vector x = [0, 2, 4, 6]. To create a row vector z consisting of the values from 5 to 8 in steps of 0. 1, type z = [5: 0. 1: 8]. >>x = [m: q: n] If the increment q is omitted, it is presumed to be 1. Thus typing y = [ 3: 2] produces the vector y = [ 3, 2, 1, 0, 1, 2]. 2 -7

MATLAB 程式設計與 程應用 The linspace command also creates a linearly spaced row vector, but instead you specify the number of values rather than the increment. The syntax is linspace(x 1, x 2, n), where x 1 and x 2 are the lower and upper limits and n is the number of points. For example, linspace(5, 8, 31) is equivalent to [5: 0. 1: 8]. If n is omitted, the spacing is 1.

MATLAB 程式設計與 程應用 The logspace command creates an array of logarithmically spaced elements. Its syntax is logspace(a, b, n), where n is the number of points between 10 a and 10 b. For example, x = logspace( 1, 1, 4) produces the vector x = [0. 1000, 0. 4642, 2. 1544, 10. 000]. If n is omitted, the number of points defaults to 50.

MATLAB 程式設計與 程應用 矩陣的建立 If the matrix is small you can type it row by row, separating the elements in a given row with spaces or commas and separating the rows with semicolons. For example, typing >>A = [2, 4, 10; 16, 3, 7]; creates the following matrix: A= 2 4 10 16 3 7 Remember, spaces or commas separate elements in different columns, whereas semicolons separate elements in different rows.

MATLAB 程式設計與 程應用 向量的長度、大小與絕對值 Keep in mind the precise meaning of these terms when using MATLAB. The length command gives the number of elements in the vector. The magnitude of a vector x having elements x 1, x 2, …, xn is a scalar, given by (x 12 + x 22 + … + xn 2), and is the same as the vector's geometric length. The absolute value of a vector x is a vector whose elements are the absolute values of the elements of x.

MATLAB 程式設計與 程應用 範例 x = [2, 4, 5], its length is 3; (computed from length(x)) its magnitude is [22 + (– 4)2 + 52] = 6. 7082; (computed from sqrt(x’*x)) its absolute value is [2, 4, 5] (computed from abs(x)).

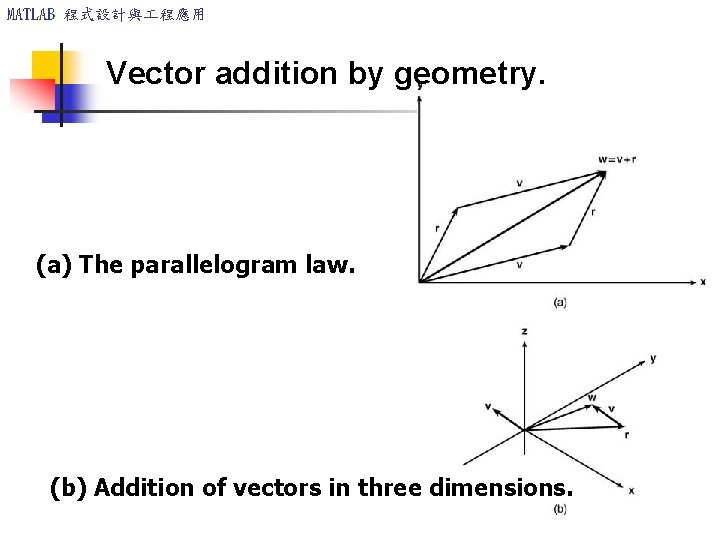
MATLAB 程式設計與 程應用 Vector addition by geometry. (a) The parallelogram law. (b) Addition of vectors in three dimensions.

MATLAB 程式設計與 程應用 Array Addition and Subtraction 6 – 2 10 3 + 9 8 – 12 14 = 15 6 – 2 17 Array subtraction is performed in a similar way. The addition shown performed in MATLAB as follows: >>A = [6, 2; 10, 3]; >>B = [9, 8; 12, 14] >>A+B ans = 15 6 2 17

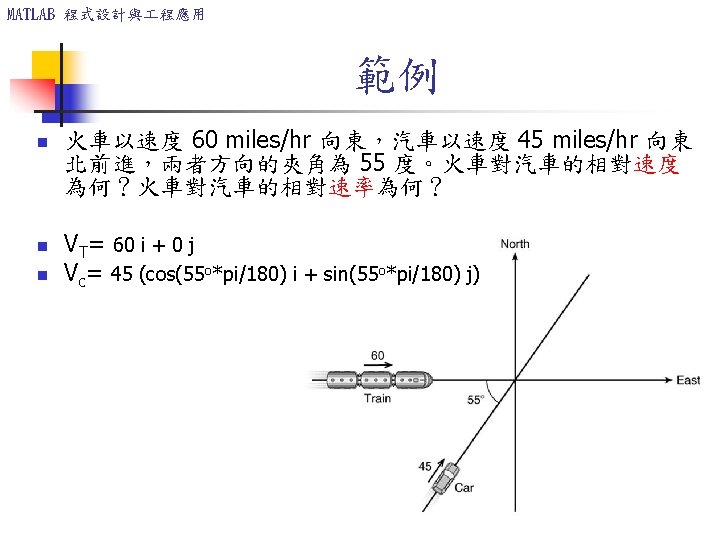
MATLAB 程式設計與 程應用 範例 n n n VT= [60, 0]; Vc= 45 * [cos(55 o*pi/180), sin(55 o*pi/180)]; V R= V T – V c S 1 R=sqrt(VR’*VR) S 2 R=sqrt(VR(1)^2+VR(2)^2) S 3 R=sqrt(sum(VR. *VR))

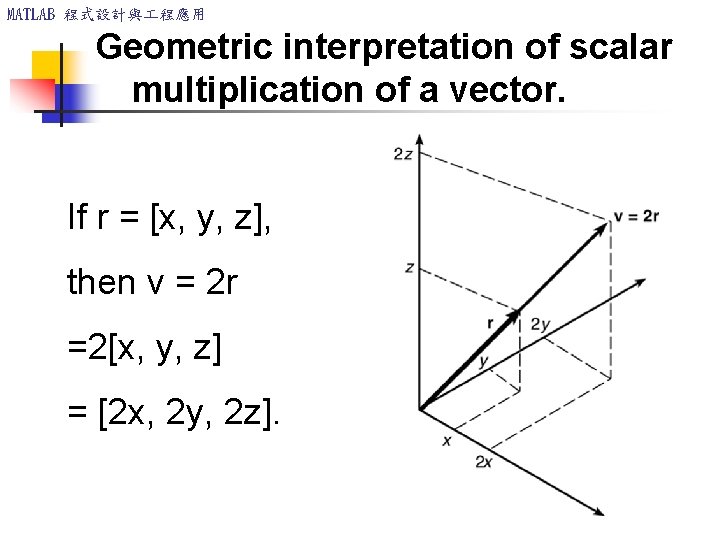
MATLAB 程式設計與 程應用 Geometric interpretation of scalar multiplication of a vector. If r = [x, y, z], then v = 2 r =2[x, y, z] = [2 x, 2 y, 2 z].

MATLAB 程式設計與 程應用 scalar multiplication of a vector 2 9 3 5 – 7 = 6 27 15 – 21 This multiplication is performed in MATLAB as follows: >>A = [2, 9; 5, 7]; >>3*A ans = 6 27 15 21

MATLAB 程式設計與 程應用 Array Index >>u = [0: 0. 1: 10]; w = 5*sin(u); >>u(7) ans = 0. 6000 >>w(7) ans = 2. 8232 • 使用 length 函數來瞭解陣列的長度. >>m = length(w) m = 101

MATLAB 程式設計與 程應用 兩種乘法的定義 1. array multiplication (element-by-element multiplication), 2. matrix multiplication.

MATLAB 程式設計與 程應用 Element-by-element operations Symbol Operation Form Examples + Scalar-array addition A + b [6, 3]+2=[8, 5] Scalar-array subtraction A – b [8, 3] 5=[3, 2] + Array addition A + B [6, 5]+[4, 8]=[10, 13] Array subtraction A – B [6, 5] [4, 8]=[2, 3] . * Array multiplication A. *B [3, 5]. *[4, 8]=[12, 40] . / Array right division A. /B [2, 5]. /[4, 8]=[2/4, 5/8] . Array left division A. B [2, 5]. [4, 8]=[24, 58] . ^ Array exponentiation A. ^B [3, 5]. ^2=[3^2, 5^2] 2. ^[3, 5]=[2^3, 2^5] [3, 5]. ^[2, 4]=[3^2, 5^4]

MATLAB 程式設計與 程應用 Element-by-element multiplication Array or Element-by-element multiplication is defined only for arrays having the same size. The definition of the product x. *y, where x and y each have n elements, is x. *y = [x(1)y(1), x(2)y(2), . . . , x(n)y(n)] if x and y are row vectors. For example, if x = [2, 4, – 5], y = [– 7, 3, – 8] then z = x. *y gives z = [2(– 7), 4 (3), – 5(– 8)] = [– 14, 12, 40]

MATLAB 程式設計與 程應用 Element-by-element multiplication If x and y are column vectors, the result of x. *y is a column vector. For example z = (x’). *(y’) gives z = 2(– 7) 4(3) – 5(– 8) = – 14 12 40 Note that x’ is a column vector with size 3 × 1 and thus does not have the same size as y, whose size is 1 × 3. Thus for the vectors x and y the operations x’. *y and y. *x’ are not defined in MATLAB and will generate an error message.

MATLAB 程式設計與 程應用 Element-by-element multiplication The array multiplication operation A. *B results in a matrix C that has the same size as A and B and has the elements ci j = ai j bi j. For example, if A = 11 5 – 9 4 B = – 7 8 6 2 then C = A. *B gives this result: C = 11(– 7) 5(8) = – 77 40 – 9(6) 4(2) – 54 8

MATLAB 程式設計與 程應用 Array Division The symbol for array right division is. /. For example, if x = [8, 12, 15] y = [– 2, 6, 5] then z = x. /y gives z = [8/(– 2), 12/6, 15/5] = [– 4, 2, 3] Also, if A = 24 20 – 9 4 B = – 4 5 3 2 then C = A. /B gives C = 24/(– 4) 20/5 = – 6 4 – 9/3 4/2 – 3 2

MATLAB 程式設計與 程應用 Solution of Linear Algebraic Equations 6 x + 12 y + 4 z = 70 7 x – 2 y + 3 z = 5 2 x + 8 y – 9 z = 64 >>A = [6, 12, 4; 7, 2, 3; 2, 8, 9]; >>B = [70; 5; 64]; >>Solution = AB AX=B Solution = 3 -1 B X = A 5 2 The solution is x = 3, y = 5, and z = – 2.

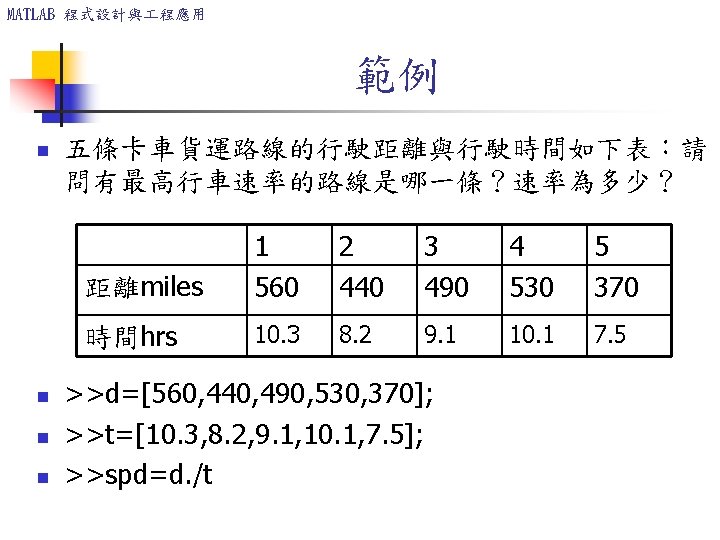
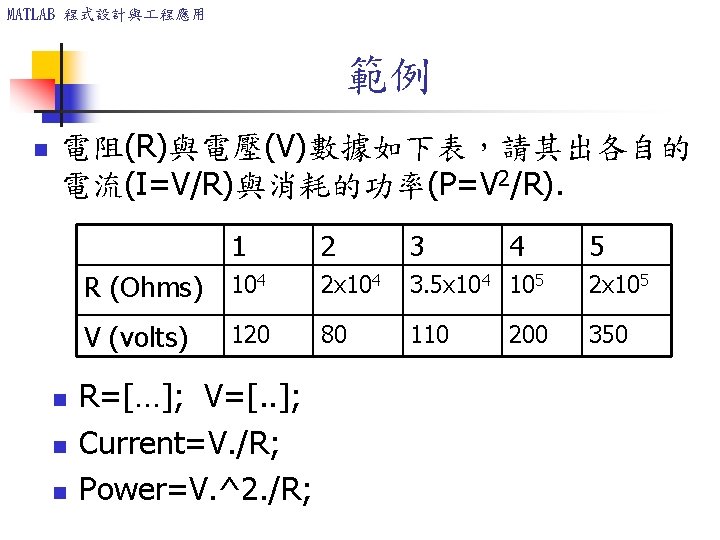
MATLAB 程式設計與 程應用 範例 n 電阻(R)與電壓(V)數據如下表，請其出各自的 電流(I=V/R)與消耗的功率(P=V 2/R). n n n 1 2 3 R (Ohms) 104 2 x 104 3. 5 x 104 105 2 x 105 V (volts) 120 80 110 350 R=[…]; V=[. . ]; Current=V. /R; Power=V. ^2. /R; 4 200 5

MATLAB 程式設計與 程應用 Array Exponentiation To perform exponentiation on an element-by-element basis, we must use the. ^ symbol. For example, if x = [3, 5, 8], then typing x. ^3 produces the array [33, 53, 83] = [27, 125, 512]. if p = [2, 4, 5], then typing 3. ^p produces the array [32, 34, 35] = [9, 81, 243]. 3. ^p 3. 0. ^p 3. . ^p (3). ^p 3. ^[2, 4, 5] 結果都一樣 你看得出來嗎？

MATLAB 程式設計與 程應用 範例 v= [10: 2: 20]; th=[50: 10: 80]; thr=th*(pi/180); g=9. 8; vel=[]; %create the 6 x 4 array of speeds for k=1: length(thr) vel=[vel, v’]; end theta=[]; %create the 6 x 4 array of angles for k=1: length(v) Theta=[theta; thr]; end h=(vel. ^2. *(sin(theta)). ^2)/(2*g); h=[v’, h]; table=[0, th; H)

MATLAB 程式設計與 程應用 Matrix Multiplication In the product of two matrices AB, the number of columns in A must equal the number of rows in B. The row-column multiplications form column vectors, and these column vectors form the matrix result. The product AB has the same number of rows as A and the same number of columns as B. For example, 6 – 2 9 8 10 3 – 5 12 4 7 (6)(9) + (– 2)(– 5) (6)(8) + (– 2)(12) = (10)(9) + (3)(– 5) (10)(8) + (3)(12) (4)(9) + (7)(– 5) (4)(8) + (7)(12) 64 24 = 75 116 1 116

MATLAB 程式設計與 程應用 Matrix Multiplication Use the operator * to perform matrix multiplication in MATLAB. >>A = [6, 2; 10, 3; 4, 7]; >>B = [9, 8; 5, 12]; >>A*B ans = 64 24 75 116 1 116

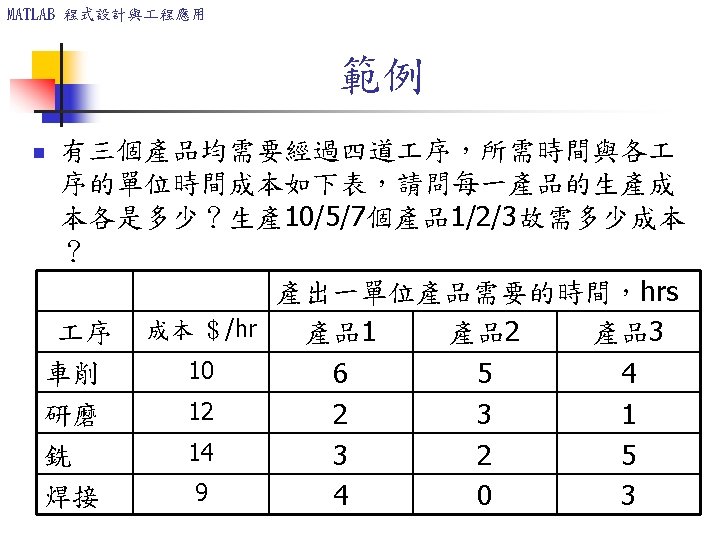
MATLAB 程式設計與 程應用 範例 n n n A=[10, 12, 14, 9]; % hourly cost B=[6 2 3 4; 5 3 2 0; 4 1 5 3]; %time required unit. Cst=A*B’ %answer is [162 114 149] C=[10 5 7]; %No. of items total. Cst=C*unit. Cst’%answer is 3233

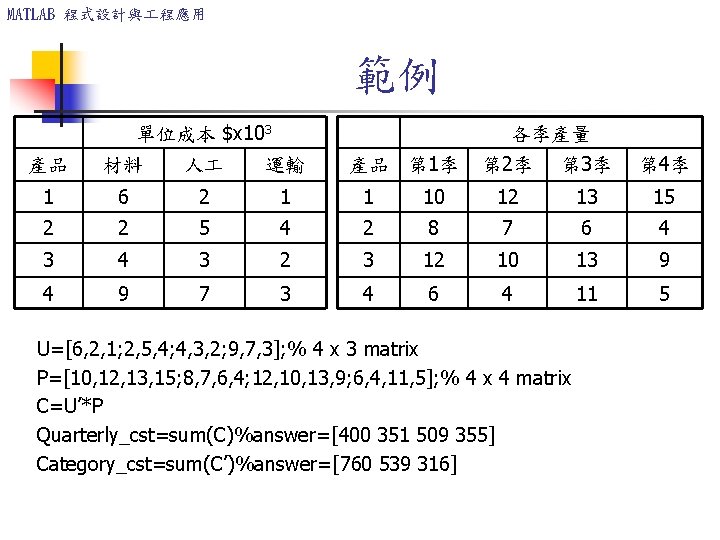
MATLAB 程式設計與 程應用 範例 單位成本 $x 103 各季產量 產品 材料 人 運輸 產品 第 1季 第 2季 第 3季 第 4季 1 6 2 1 1 10 12 13 15 2 2 5 4 2 8 7 6 4 3 2 3 12 10 13 9 4 9 7 3 4 6 4 11 5 U=[6, 2, 1; 2, 5, 4; 4, 3, 2; 9, 7, 3]; % 4 x 3 matrix P=[10, 12, 13, 15; 8, 7, 6, 4; 12, 10, 13, 9; 6, 4, 11, 5]; % 4 x 4 matrix C=U’*P Quarterly_cst=sum(C)%answer=[400 351 509 355] Category_cst=sum(C’)%answer=[760 539 316]

MATLAB 程式設計與 程應用 Matrix multiplication does not have the commutative property that is, in general, AB ¹ BA. A simple example will demonstrate this fact: AB = 6 – 2 10 3 9 8 = 78 20 – 12 14 54 122 whereas BA = 9 8 – 12 14 6 – 2 10 3 = 134 6 68 65 Reversing the order of matrix multiplication is a common and easily made mistake.

MATLAB 程式設計與 程應用 Two exceptions to the noncommutative property • the null or zero matrix, denoted by 0 • the identity, or unity, matrix, denoted by I. The null matrix contains all zeros and is not the same as the empty matrix [ ], which has no elements. These matrices have the following properties: 0 A = A 0 = 0 IA = AI = A

MATLAB 程式設計與 程應用 The identity matrix is a square matrix whose diagonal elements are all equal to one, with the remaining elements equal to zero. For example, the 2 × 2 identity matrix is I = 1 0 0 1 The functions eye(n) and eye(size(A)) create an n × n identity matrix and an identity matrix the same size as the matrix A.

MATLAB 程式設計與 程應用 Array Addressing The colon operator selects individual elements, rows, columns, or ''subarrays'' of arrays. Here are some examples: n n n v(: ) represents all the row or column elements of the vector v. v(2: 5) represents the second through fifth elements; that is v(2), v(3), v(4), v(5). A(: , 3) denotes all the elements in the third column of the matrix A. A(: , 2: 5) denotes all the elements in the second through fifth columns of A. A(2: 3, 1: 3) denotes all the elements in the second and third rows that are also in the first through third columns.

MATLAB 程式設計與 程應用 You can use array indices to extract a smaller array from another array. For example, if you first create the array B 2 4 10 13 B = 16 3 7 18 8 4 9 25 3 12 15 17 then type C = B(2: 3, 1: 3), you can produce the following array: C= 16 3 7 8 4 9

MATLAB 程式設計與 程應用 m x n矩陣的各種處理(續3) n n n n array 1=[1. 1 -2. 2 array 1(3)=? array 1([1 4])=? array 1(1: 2: 5)=? 3. 3 -4. 4 5. 5]; [3. 3] [1. 1 -4. 4] [1. 1 3. 3 5. 5] arr 2=[1 2 3; -2 -3 -4; 3 4 5]; arr 2(1, : )=? [1 2 3] arr 2(: , 1: 2: 3)=? [1 3; -2 -4; 3 5]

MATLAB 程式設計與 程應用 m x n矩陣的各種處理5 n n n n n >>arr 3=[1 2 3 4 5 6 7 8]; arr 3(5: end)=[5 6 7 8] arr 3(end)=[8] >>arr 4=[1 2 3 4; 5 6 7 8; 9 10 11 12]; arr 4(2: end; 2: end)=? [6 7 8; 10 11 12] >>arr 4(1: 2, [1 4])=[20 21; 22 23]; arr 4 =? [20 2 3 21; 22 6 7 23; 9 10 11 12] >>arr 4=[20 21; 22 23]; arr 4=?

MATLAB 程式設計與 程應用 m x n矩陣的各種處理6 n n n >>arr 4=[1 2 3 4; 5 6 7 8; 9 10 11 12]; >>arr 4(1: 2, 1: 2)=1 arr 4= 1 1 3 4 1 1 7 8 9 10 11 12

MATLAB 程式設計與 程應用 m x n矩陣的各種處理7 n n n n >>arr 5=zeros(4) >>arr 6=ones(4) >>arr 7=eye(4) % 單元矩陣 比較 length(arr? ) 與 size(arr? )的差別 >>arr 5=zeros(3, 4) >>arr 6=ones(3, 4) >>arr 7=eye(3, 4) 比較 length(arr? ) 與 size(arr? )的差別

MATLAB 程式設計與 程應用 Array Functions size(A) Returns a row vector [m n] containing the sizes of the m x n array A. sort(A) Sorts each column of the array A in ascending order and returns an array the same size as A. sum(A) Sums the elements in each column of the array A and returns a row vector containing the sums. max(A) Returns the algebraically largest element in A if A is a vector. Returns a row vector containing the largest elements in each column if A is a matrix. If any of the elements are complex, max(A) returns the elements that have the largest magnitudes. min(A) Like max but returns minimum values. Length(A) Computes either the number of elements of A is a vector or the largest value of m or n if A is an m × n matrix.

MATLAB 程式設計與 程應用 Advanced Array Functions [b, k] = sort(A) Sorts each column of the array A in ascending order and returns a row vector b and their indices in the row vector k. [x, k] = max(A) Similar to max(A) but stores the maximum values in the row vector x and their indices in the row vector k. [x, k] = min(A) Like max but returns minimum values. [u, v, w] = find(A) Computes the arrays u and v, containing the row and column indices of the nonzero elements of the matrix A, and the array w, containing the values of the nonzero elements. The array w may be omitted.

MATLAB 程式設計與 程應用 練習 6 2 A = – 10 0 3 – 5 max(A) returns the vector [6, 2]; min(A) returns the vector [-10, -5]; size(A) returns [3, 2]; length(A) returns 3. sum(A) returns [-1 -3] 得到”行加總” 請問如何求列加總 ？ sum(A’)’

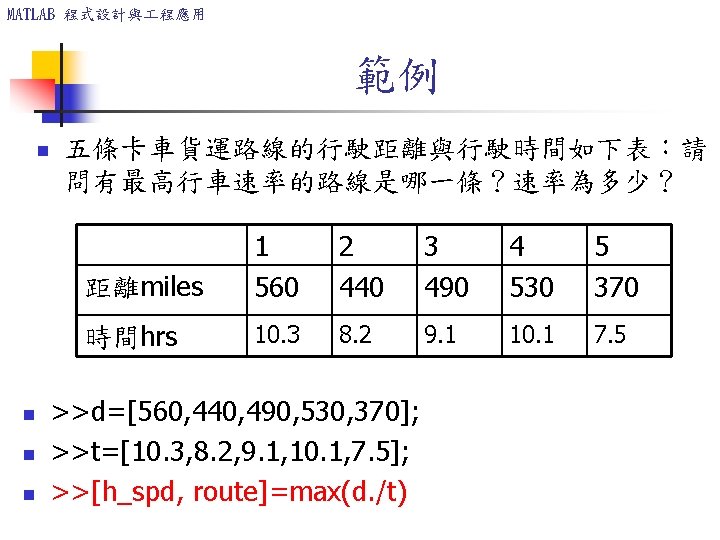
MATLAB 程式設計與 程應用 Vectorized functions The built-in MATLAB functions such as sqrt(x) and exp(x) automatically operate on array arguments to produce an array result the same size as the array argument x. Thus these functions are said to be vectorized functions. For example, in the following session the result y has the same size as the argument x. >>x = [4, 16, 25]; >>y = sqrt(x) y = 2 4 5

MATLAB 程式設計與 程應用 When multiplying or dividing vectorized functions, or when raising them to a power, you must use element-by-element operations if the arguments are arrays. For example, to compute z = (ey sin x) cos 2 x, you must type z = exp(y). *sin(x). *(cos(x)). ^2. You will get an error message if the size of x is not the same as the size of y. The result z will have the same size as x and y.

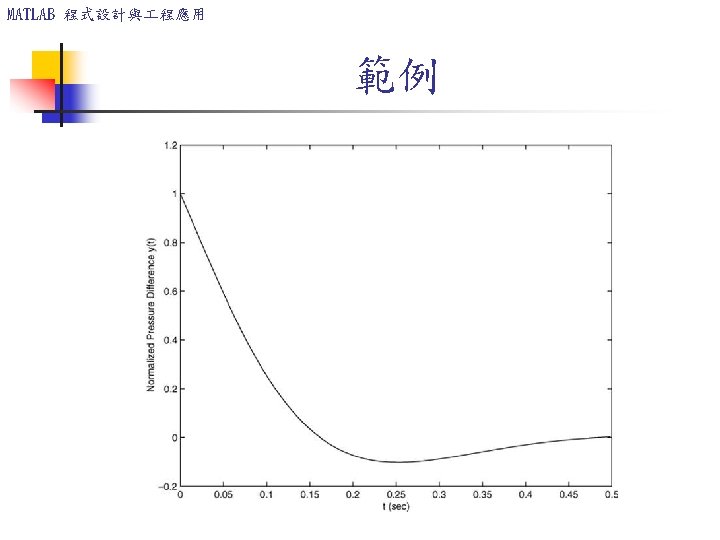
MATLAB 程式設計與 程應用 Order of Precedence Operation First Parentheses, evaluated starting with the innermost pair. Second Exponentiation, evaluated from left to right. Third Multiplication and division with equal precedence, evaluated from left to right. Fourth Addition and subtraction with equal precedence, evaluated from left to right.

MATLAB 程式設計與 程應用 Examples of Precedence >> 8 + 3*5 ans = 23 >> 8 + (3*5) ans = 23 >>(8 + 3)*5 ans = 55 >>4^2 12 8/4*2 ans = 0 >>4^2 12 8/(4*2) ans = 3 >> 3*4^2 + 5 ans = 53 >>(3*4)^2 + 5 ans = 149 >>27^(1/3) + 32^(0. 2) ans = 5 >>27^(1/3) + 32^0. 2 ans = 5 >>27^1/3 + 32^0. 2 ans = 11

MATLAB 程式設計與 程應用 Function MATLAB syntax ex exp(x) √x sqrt(x) ln x log(x) log 10 x log 10(x) cos x cos(x) sin x sin(x) tan x tan(x) cos-1 x acos(x) sin-1 x asin(x) tan-1 x atan(x) The MATLAB trigonometric functions use radian measure.

MATLAB 程式設計與 程應用 數學函數 n n n cos(x) sin(x) tan(x) sec(x) csc(x) cot(x) acos(x) asin(x) atan 2(y, x) exp(x) log 10(x) log 2(x) sqrt(x) cosh(x) sinh(x) tanh(x) sech(x) csch(x) coth(x) acosh(x) asinh(x) atanh(x) sign(x) airy(n, x) besselh(n, x) besseli(n, x) besselj(n, x) besselk(n, x) bessely(n, x) beta(x, y) betainc(x, y, z) betaln(x, y) ellipj(x, m) ellipke(x) erfc(x) erfcx(x) erfinv(x) gammainc(x, a) gammaln (x) expint(x) legendre(n, x) factorial(x)

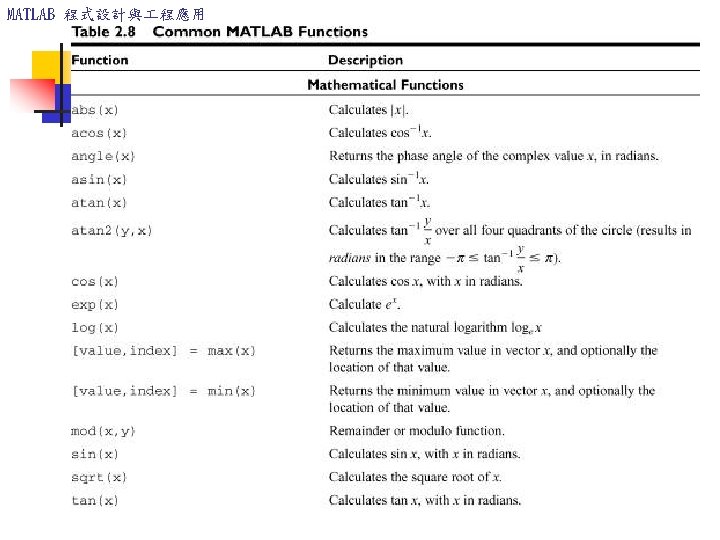
MATLAB 程式設計與 程應用 Common MATLAB functions

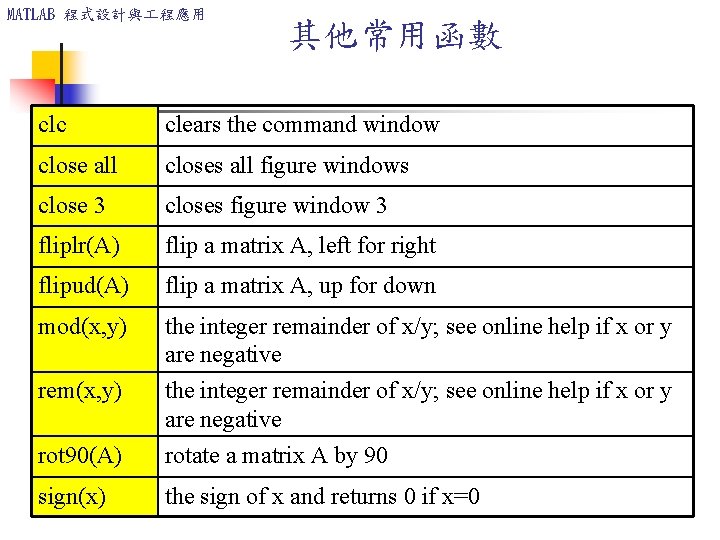
MATLAB 程式設計與 程應用 其他常用函數 clc clears the command window close all closes all figure windows close 3 closes figure window 3 fliplr(A) flip a matrix A, left for right flipud(A) flip a matrix A, up for down mod(x, y) the integer remainder of x/y; see online help if x or y are negative rem(x, y) rot 90(A) rotate a matrix A by 90 sign(x) the sign of x and returns 0 if x=0

MATLAB 程式設計與 程應用 Relational operators Relational Meaning operator < <= > >= == ~= Less than or equal to. Greater than or equal to. Equal to. Not equal to.

MATLAB 程式設計與 程應用 Relational Operators 練習 >> x = [6, 3, 9]; y = [14, 2, 9]; >> z = (x < y) z = 1 0 0 >>z = (x > y) z = 0 1 0 >>z = (x ~= y) z = 1 1 0 >>z = (x == y) z = 0 0 1 >>z = (x > 8) z = 0 0 1

MATLAB 程式設計與 程應用 Keep in mind when using script files 1. The name of a script file must begin with a letter, and may include digits and the underscore character, up to 31 characters. 2. Do not give a script file the same name as a variable. 3. Do not give a script file the same name as a MATLAB command or function. You can check to see if a command, function or file name already exists by using the exist command.

MATLAB 程式設計與 程應用 Debugging Script Files Program errors usually fall into one of the following categories. 1. Syntax errors such as omitting a parenthesis or comma, or spelling a command name incorrectly. MATLAB usually detects the more obvious errors and displays a message describing the error and its location. 2. Errors due to an incorrect mathematical procedure, called runtime errors. Their occurrence often depends on the particular input data. A common example is division by zero.

MATLAB 程式設計與 程應用 To locate program errors try the following: 1. Test your program with a simple version of the problem which can be checked by hand. 2. Display any intermediate calculations by removing semicolons at the end of statements. 3. Use the debugging features of the Editor/Debugger.

MATLAB 程式設計與 程應用 Input/output commands disp(A) Displays the contents, but not the name, of the array A. disp(’text’) Displays the text string enclosed within quotes. x = input(’text’) Displays the text in quotes, waits for user input from the keyboard, and stores the value in x. x= Displays the text in quotes, waits for input(’text’, ’s’) user input from the keyboard, and stores the input as a string in x.

MATLAB 程式設計與 程應用 fprintf 指令 n n n n fprintf(’ fprintf(’ N =%g n’, 500) x =%1. 12 g n’, pi) x =%1. 10 e n’, pi) x =%6. 2 f n’, pi) x =%12. 8 f y =%12. 8 f n’, 5, exp(5)) Note: n is the command for a new line. For full information type >>help fprintf

MATLAB 程式設計與 程應用 M file範例：自由落體運動 計算公式為 v = gt. 繪圖表示 v = f(t) for 0 ≤ tf, 其中 tf 為使 用者指定的最終時間 % Program falling_speed. m: % Plots speed of a falling object. % Input Variable: tf = final time (in sec. ) % Output Variables: % t = array of times at which speed is computed (in sec. ) % v = array of speeds (m/s) % Create an array of 501 time values. % Parameter Value: t = [0: dt: tf]; g = 9. 81; % Acceleration in SI units % Compute speed values. % v = g*t; % Input section: tf = input(’Enter final time in seconds: ’); % % Output section: % Calculation section: Plot(t, v), xlabel(’t (s)’), ylabel(’v m/s)’) dt = tf/500;

MATLAB 程式設計與 程應用 my. Test. m n n n % my. Test: my first test M-file. fprintf('Start of my. Test. m!n'); for i = 1: 3 fprintf('i = %d ---> i^3 = %dn', i, i^3); end fprintf('End of my. Test. m!n');

MATLAB 程式設計與 程應用 fact 01. m n function output = fact 01(n) n % FACT 01 Calculate factorial of a given positive integer (for-loop version) n n output = 1; for i = 1: n, output = output*i; end

MATLAB 程式設計與 程應用 fact 02. m n n n n function output = fact 02(n) % FACT 2 Calculate factorial of a given positive integer (recursive version) if n == 1, % Terminating condition output = 1; return; end output = n*fact 02(n-1);

MATLAB 程式設計與 程應用 寫一個 程式 find. N 01. m，求 n! > realmax的最小n 值 n 請問 n 值是多少？此時 (n-1)! 的值又是多少？ function find. N 01 max. N = 1000; for n=1: max. N value = prod(1: n); if value>realmax break; end fprintf('n = %dn', n); fprintf('(n-1)! = %dn', prod(1: n-1));

MATLAB 程式設計與 程應用 函數 prod n n Prod(1: 2) Prod(1: 3) Prod(1: 4) Prod(1: 10 ) n n fact 01(2) fact 01(3) fact 01(4) fact 01(10) n n fact 02(2) fact 02(3) fact 02(4) fact 02(10)

MATLAB 程式設計與 程應用 End of Chapter 2

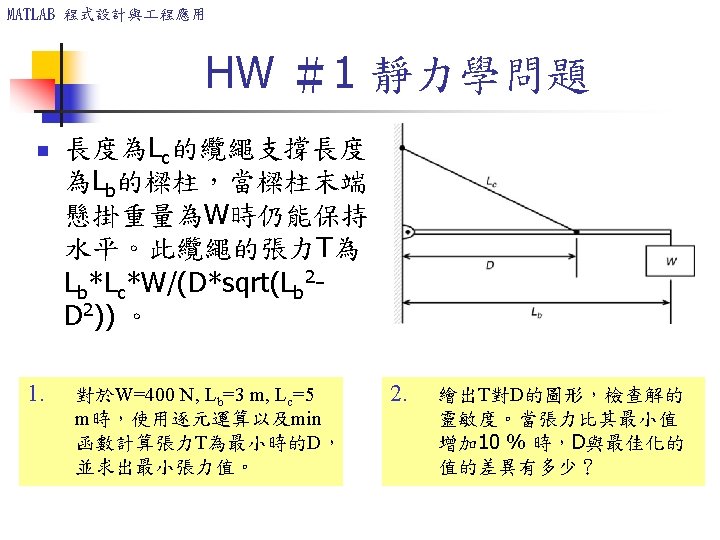
MATLAB 程式設計與 程應用 寫一個 遞迴函數 fibo. m 來計算 Fibonacci 數列 定義如下：fibo(n+2) = fibo(n+1)+fibo(n) 此數列的啟始條件：fibo(1) = 0, fibo(2) = 1. 使用 tic 和 toc 指令來測量 fibo(25) 的計算時間。 function out = fibo(n) % fibo: Fibonacci number if n==1 out=0; return; elseif n==2 out=1; return; else out=fibo(n-1)+fibo(n-2); end

MATLAB 程式設計與 程應用 寫一個非遞迴函數 fibo 2. m 來計算 Fibonacci 數列的第 n 項可以直接表示成 fibo 2(n)={[(1+a)/2]^(n-1)-[(1 -a)/2]^(n-1)}/a 其中 a 是 5 的平方根。 請計算 fibo 2(25) 的計算時間，並和 fibo(25) 比較。 function out = fibo 2(n) % Fibonacci number using an analytic expression r 1=(1+sqrt(5))/2; r 2=(1 -sqrt(5))/2; out=(r 1^(n-1)-r 2^(n-1))/sqrt(5);

MATLAB 程式設計與 程應用 請寫一個函數 minxy. m， 其功能是由一個二維矩陣中找出小元素 [min. Value, min. Index] = minxy(matrix) 其中 matrix 是一個二維矩陣，min. Value 則是其元素的最小值，而 min. Index 是 長 度 為 2 的 正 整 數 向 量 ， 代 表 最 小 值 的 索 引 。 換 句 話 說 ， matrix(min. Index(1), min. Index(2)) 的值即是 min. Value。 請測試 [min. Value, min. Index] = minxy(magic(20)) 所傳回來的 min. Value 和 min. Index 各是多少？ function [min. Value, min. Index] = minxy(matrix) %Minimum of a 2 D matrix % Usage: [min. Value, min. Index] = minxy(A) % min. Value: the minimum of the matrix A % min. Index: the 2 D index of min. Value in A [column. Min, column. Min. Index] = min(matrix); [min. Value, tmp] = min(column. Min); min. Index = [column. Min. Index(tmp) tmp];

MATLAB 程式設計與 程應用 請寫一個函數 ranking 01. m， 輸入為成績向量 x，輸出則是此成績的排名 function out = ranking 01(x) % ranking: Ascending ranking of element of x % x = [92, 95, 58, 75, 69, 82] 時，ranking 01(x) 回傳的排名向量則是 % [2, 1, 6, 4, 5, 3]，代表 92 分是排名第 2，82 分是排名第 3。 [sorted, position]=sort(-x); % 由大到小排列 n=length(x); rank=1: n; [junk, index]=sort(position); out=rank(index);

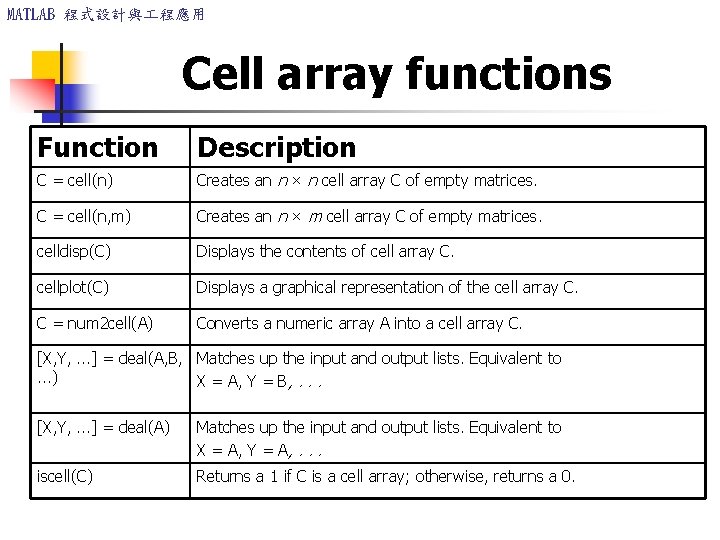
MATLAB 程式設計與 程應用 Cell array functions Function Description C = cell(n) Creates an n × n cell array C of empty matrices. C = cell(n, m) Creates an n × m cell array C of empty matrices. celldisp(C) Displays the contents of cell array C. cellplot(C) Displays a graphical representation of the cell array C. C = num 2 cell(A) Converts a numeric array A into a cell array C. [X, Y, . . . ] = deal(A, B, Matches up the input and output lists. Equivalent to. . . ) X = A, Y = B, . . . [X, Y, . . . ] = deal(A) Matches up the input and output lists. Equivalent to X = A, Y = A, . . . iscell(C) Returns a 1 if C is a cell array; otherwise, returns a 0.

MATLAB 程式設計與 程應用 Arrangement of data in the structure array student

MATLAB 程式設計與 程應用 Structure functions Function Description names = fieldnames(S) Returns the field names associated with the structure array S as names, a cell array of strings. F = getfield(S, ’field’) Returns the contents of the field ’field’ in the structure array S. Equivalent to F = S. field. isfield(S, ’field’) Returns 1 if ’field’ is the name of a field in the structure array S, and 0 otherwise.

MATLAB 程式設計與 程應用 Structure functions Function Description S = rmfield(S, ’field’) Removes the field ’field’ from the structure array S. S = setfield(S, ’field’, V) Sets the contents of the field ’field’ to the value V in the structure array S. S = struct(’f 1’, ’v 1’, ’f 2’, ’v 2’, . . . ) Creates a structure array with the fields ’f 1’, ’f 2’, . . . having the values ’v 1’, ’v 2’, . .

MATLAB 程式設計與 程應用 MATLAB 也支援複數運算 • The number c 1 = 1 – 2 i is entered as follows: c 1 = 1 2 i. • An asterisk is not needed between i or j and a number, although it is required with a variable, such as c 2 = 5 i*c 1. • Be careful. The expressions y = 7/2*i and x = 7/2 i give two different results: y = (7/2)i = 3. 5 i and x = 7/(2 i) = – 3. 5 i.

MATLAB 程式設計與 程應用 Euler Identity 尤拉恆等式 n >> y = exp(j*pi/6) % y= 0. 8660 + 0. 5000 i

MATLAB 程式設計與 程應用 Solution to HW#1 W = 400; Lb = 3; Lc = 5; D = [0: 0. 01: Lb]; T = Lb*Lc*W. /(D. *sqrt(Lb^2 -D. ^2)); [min. T, k] = min(T) min. D = D(k) The solution is min. T = 1. 3333 e+003 and min. D = 2. 12, which correspond to a tension of T = 1333 N and a distance of D = 2. 12 m.

MATLAB 程式設計與 程應用 b) Append the following lines to the script file in part (a). Dplot = [1. 5: 0. 001: 2. 2]; upper = 1. 1*min. T Tplot = Lb*Lc*W. /(Dplot. *sqrt(Lb^2 -Dplot. ^2)); plot(Dplot, Tplot, [1. 5, 2. 2], [upper, upper]), grid The upper tension value is 1. 1(1333) = 1467 N. The intersection of the two lines on the plot gives the solution, which is approximately D = 1. 6 m (1. 62 is a more accurate value).