MATLAB Optimization Toolbox Presented by Chin Pei February

MATLAB Optimization Toolbox Presented by Chin Pei February 28, 2003

Presentation Outline n Introduction n n Function Optimization Toolbox Routines / Algorithms available Minimization Problems n n Unconstrained Constrained n n n Example The Algorithm Description Multiobjective Optimization n Optimal PID Control Example

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Function Optimization n n Optimization concerns the minimization or maximization of functions Standard Optimization Problem Subject to: Equality Constraints Inequality Constraints Side Constraints

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Function Optimization is the objective function, which measure and evaluate the performance of a system. In a standard problem, we are minimizing the function. For maximization, it is equivalent to minimization of the –ve of the objective function. is a column vector of design variables, which can affect the performance of the system.

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Function Optimization Constraints – Limitation to the design space. Can be linear or nonlinear, explicit or implicit functions Equality Constraints Inequality Constraints Most algorithm require less than!!! Side Constraints

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Optimization Toolbox n Is a collection of functions that extend the capability of MATLAB. The toolbox includes routines for: n Unconstrained optimization n Constrained nonlinear optimization, including goal attainment problems, minimax problems, and semiinfinite minimization problems n Quadratic and linear programming n Nonlinear least squares and curve fitting n Nonlinear systems of equations solving n Constrained linear least squares n Specialized algorithms for large scale problems

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Minimization Algorithm

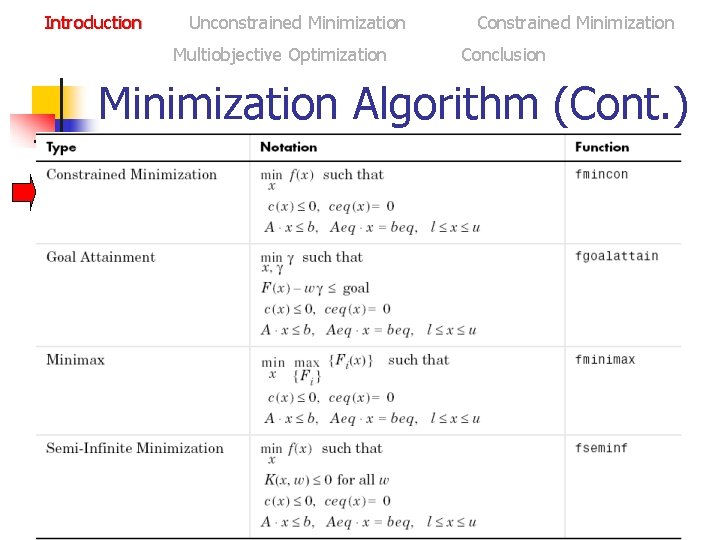
Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Minimization Algorithm (Cont. )

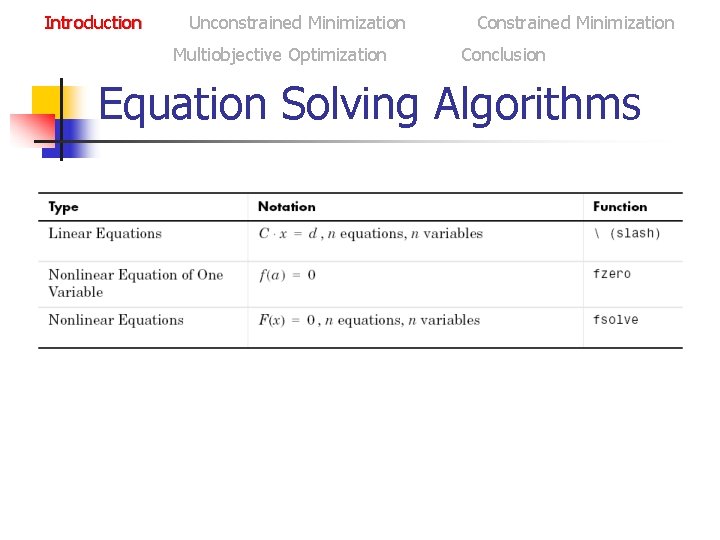
Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Equation Solving Algorithms

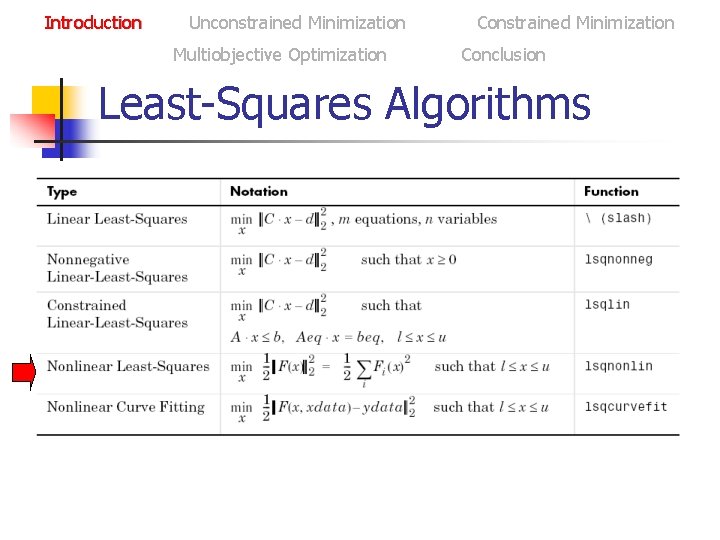
Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Least-Squares Algorithms

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Implementing Opt. Toolbox n n Most of these optimization routines require the definition of an M-file containing the function, f, to be minimized. Maximization is achieved by supplying the routines with –f. Optimization options passed to the routines change optimization parameters. Default optimization parameters can be changed through an options structure.

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Unconstrained Minimization n Consider the problem of finding a set of values [x 1 x 2]T that solves

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Steps n Create an M-file that returns the function value (Objective Function) n n Call it objfun. m Then, invoke the unconstrained minimization routine n Use fminunc

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Step 1 – Obj. Function f = objfun(x) f=exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1); Objective function

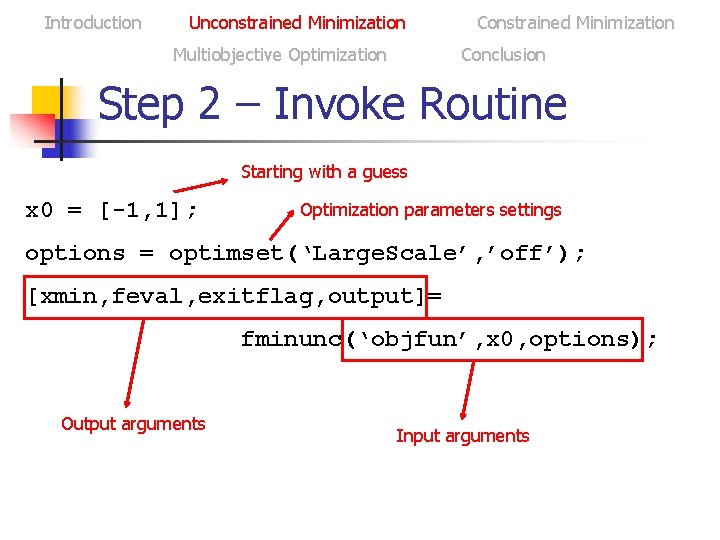
Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Step 2 – Invoke Routine Starting with a guess x 0 = [-1, 1]; Optimization parameters settings options = optimset(‘Large. Scale’, ’off’); [xmin, feval, exitflag, output]= fminunc(‘objfun’, x 0, options); Output arguments Input arguments

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Results xmin = 0. 5000 -1. 0000 Minimum point of design variables feval = Objective function value 1. 3028 e-010 exitflag = Exitflag tells if the algorithm is converged. If exitflag > 0, then local minimum is found 1 output = iterations: 7 func. Count: 40 stepsize: 1 Some other information firstorderopt: 8. 1998 e-004 algorithm: 'medium-scale: Quasi-Newton line search'

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion More on fminunc – Input [xmin, feval, exitflag, output, grad, hessian]= fminunc(fun, x 0, options, P 1, P 2, …) n n fun: Return a function of objective function. x 0: Starts with an initial guess. The guess must be a vector of size of number of design variables. option: To set some of the optimization parameters. (More after few slides) P 1, P 2, …: To pass additional parameters. Ref. Manual: Pg. 5 -5 to 5 -9

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion More on fminunc – Output [xmin, feval, exitflag, output, grad, hessian]= fminunc(fun, x 0, options, P 1, P 2, …) n n n xmin: Vector of the minimum point (optimal point). The size is the number of design variables. feval: The objective function value of at the optimal point. exitflag: A value shows whether the optimization routine is terminated successfully. (converged if >0) output: This structure gives more details about the optimization grad: The gradient value at the optimal point. hessian: The hessian value of at the optimal point Ref. Manual: Pg. 5 -5 to 5 -9

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Options Setting – optimset Options = optimset(‘param 1’, value 1, ‘param 2’, value 2, …) n n The routines in Optimization Toolbox has a set of default optimization parameters. However, the toolbox allows you to alter some of those parameters, for example: the tolerance, the step size, the gradient or hessian values, the max. number of iterations etc. There also a list of features available, for example: displaying the values at each iterations, compare the user supply gradient or hessian, etc. You can also choose the algorithm you wish to use. Ref. Manual: Pg. 5 -10 to 5 -14

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Options Setting (Cont. ) Options = optimset(‘param 1’, value 1, ‘param 2’, value 2, …) n n Type help optimset in command window, a list of options setting available will be displayed. How to read? For example: Large. Scale - Use large-scale algorithm if possible [ {on} | off ] The default is with { } Value (value 1) Parameter (param 1)

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Options Setting (Cont. ) Options = optimset(‘param 1’, value 1, ‘param 2’, value 2, …) Large. Scale - Use large-scale algorithm if possible [ {on} | off ] n Since the default is on, if we would like to turn off, we just type: Options = optimset(‘Large. Scale’, ‘off’) and pass to the input of fminunc.

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Useful Option Settings Highly recommended to use!!! n n n Display - Level of display [ off | iter | notify | final ] Max. Iter - Maximum number of iterations allowed [ positive integer ] Tol. Con - Termination tolerance on the constraint violation [ positive scalar ] Tol. Fun - Termination tolerance on the function value [ positive scalar ] Tol. X - Termination tolerance on X [ positive scalar ] Ref. Manual: Pg. 5 -10 to 5 -14

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion fminunc and fminsearch n fminunc uses algorithm with n Two modes: and hessian information. n n gradient Large-Scale: interior-reflective Newton Medium-Scale: quasi-Newton (BFGS) Not preferred in solving highly discontinuous functions. This function may only give local solutions.

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion fminunc and fminsearch n n n fminsearch is generally less efficient than fminunc for problems of order greater than two. However, when the problem is highly discontinuous, fminsearch may be more robust. This is a direct search method that does not use numerical or analytic gradients as in fminunc. This function may only give local solutions.

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Constrained Minimization Vector of Lagrange Multiplier at optimal point [xmin, feval, exitflag, output, lambda, grad, hessian] = fmincon(fun, x 0, A, B, Aeq, Beq, LB, UB, NONLCON, options, P 1, P 2, …)

Introduction Unconstrained Minimization Multiobjective Optimization Example Constrained Minimization Conclusion function f = myfun(x) f=-x(1)*x(2)*x(3); Subject to:

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Example (Cont. ) For Create a function call nonlcon which returns 2 constraint vectors [C, Ceq] function [C, Ceq]=nonlcon(x) C=2*x(1)^2+x(2); Ceq=[]; Remember to return a null Matrix if the constraint does not apply

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Example (Cont. ) Initial guess (3 design variables) x 0=[10; 10]; A=[-1 -2 -2; 1 2 2]; B=[0 72]'; LB = [0 0 0]'; UB = [30 30 30]'; [x, feval]=fmincon(@myfun, x 0, A, B, [], LB, UB, @nonlcon) CAREFUL!!! fmincon(fun, x 0, A, B, Aeq, Beq, LB, UB, NONLCON, options, P 1, P 2, …)

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Example (Cont. ) Warning: Large-scale (trust region) method does not currently solve this type of problem, switching to medium-scale (line search). > In D: ProgramsMATLAB 6 p 1toolboxoptimfmincon. m at line 213 In D: usrCHINTANGOpt. Toolboxmin_con. m at line 6 Optimization terminated successfully: Magnitude of directional derivative in search direction less than 2*options. Tol. Fun and maximum constraint violation is less than options. Tol. Const. 1 Active Constraints: Const. 2 2 9 x= 0. 00050378663220 0. 0000000 30. 0000000 feval = -4. 657237250542452 e-035 Const. 3 Const. 4 Const. 7 Const. 5 Const. 6 Const. 8 Const. 9 Sequence: A, B, Aeq, Beq, LB, UB, C, Ceq

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Multiobjective Optimization n Previous examples involved problems with a single objective function. Now let us look at solving problem with multiobjective function by lsqnonlin. Example is taken by designing an optimal PID controller for an plant.

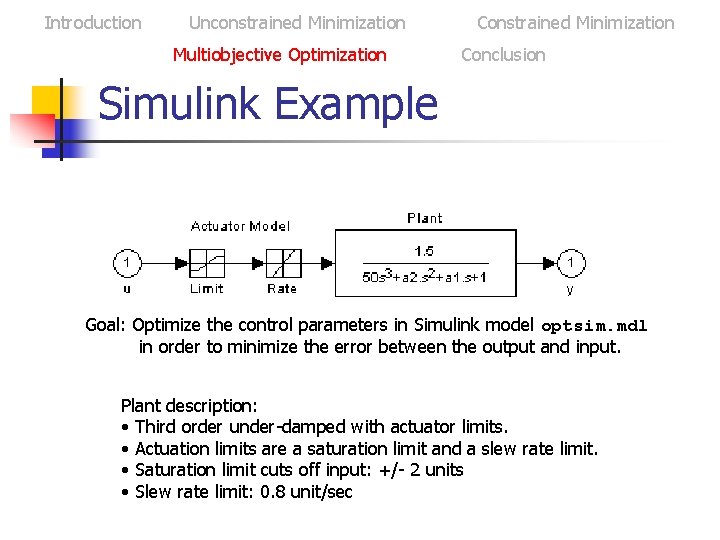
Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Simulink Example Goal: Optimize the control parameters in Simulink model optsim. mdl in order to minimize the error between the output and input. Plant description: • Third order under-damped with actuator limits. • Actuation limits are a saturation limit and a slew rate limit. • Saturation limit cuts off input: +/- 2 units • Slew rate limit: 0. 8 unit/sec

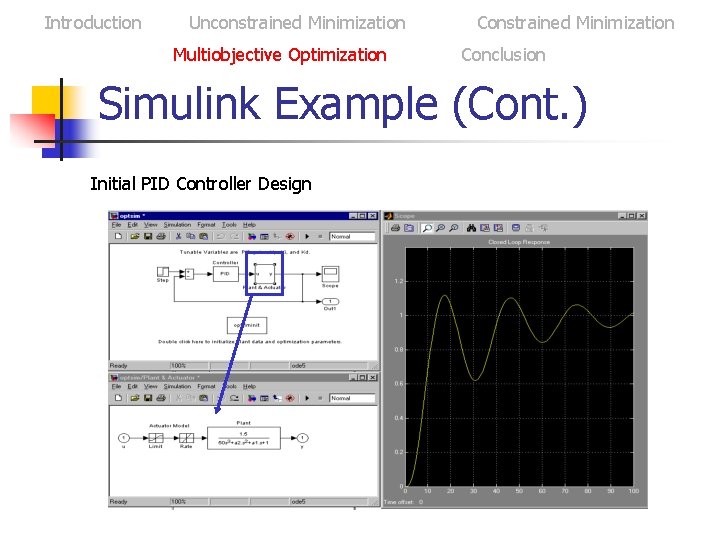
Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Simulink Example (Cont. ) Initial PID Controller Design

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Solving Methodology n n Design variables are the gains in PID controller (KP, KI and KD). Objective function is the error between the output and input.

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Solving Methodology (Cont. ) n n Let pid = [Kp Ki Kd]T Let also the step input is unity. n n F = yout - 1 Construct a function tracklsq for objective function.

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Objective Function function F = tracklsq(pid, a 1, a 2) Kp = pid(1); Ki = pid(2); Kd = pid(3); The idea is perform nonlinear least squares minimization of the errors from time 0 to 100 at the time step of 1. So, there are 101 objective functions to minimize. % Compute function value opt = simset('solver', 'ode 5', 'Src. Workspace', 'Current'); [tout, xout, yout] = sim('optsim', [0 100], opt); F = yout-1; Getting the simulation data from Simulink

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion The lsqnonlin [X, RESNORM, RESIDUAL, EXITFLAG, OUTPUT, LAMBDA, JACOBIAN] = LSQNONLIN(FUN, X 0, LB, UB, OPTIONS, P 1, P 2, . . )

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Invoking the Routine clear all Optsim; pid 0 = [0. 63 0. 0504 1. 9688]; a 1 = 3; a 2 = 43; options = optimset('Large. Scale', 'off', 'Display', 'iter', 'Tol. X', 0. 001, 'Tol. Fun ', 0. 001); pid = lsqnonlin(@tracklsq, pid 0, [], options, a 1, a 2) Kp = pid(1); Ki = pid(2); Kd = pid(3);

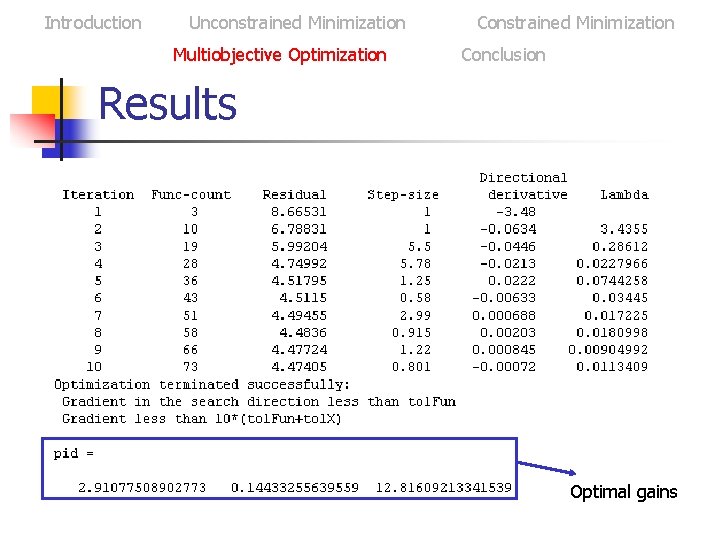
Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Results Optimal gains

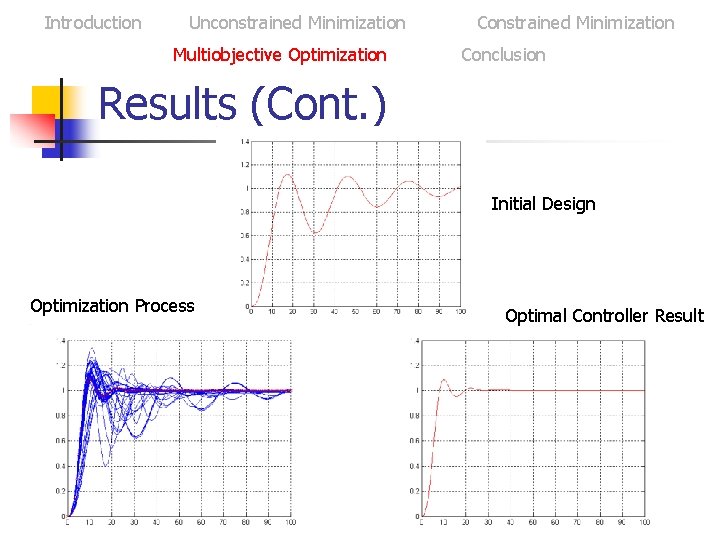
Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion Results (Cont. ) Initial Design Optimization Process Optimal Controller Result

Introduction Unconstrained Minimization Multiobjective Optimization Constrained Minimization Conclusion n n Easy to use! But, we do not know what is happening behind the routine. Therefore, it is still important to understand the limitation of each routine. Basic steps: n Recognize the class of optimization problem n Define the design variables n Create objective function n Recognize the constraints n Start an initial guess n Invoke suitable routine n Analyze the results (it might not make sense)

Thank You! Questions & Suggestions?