MATHS AND TECHNOLOGIES FOR GAMES QUATERNIONS CO 3303

MATHS AND TECHNOLOGIES FOR GAMES QUATERNIONS CO 3303 Week 1

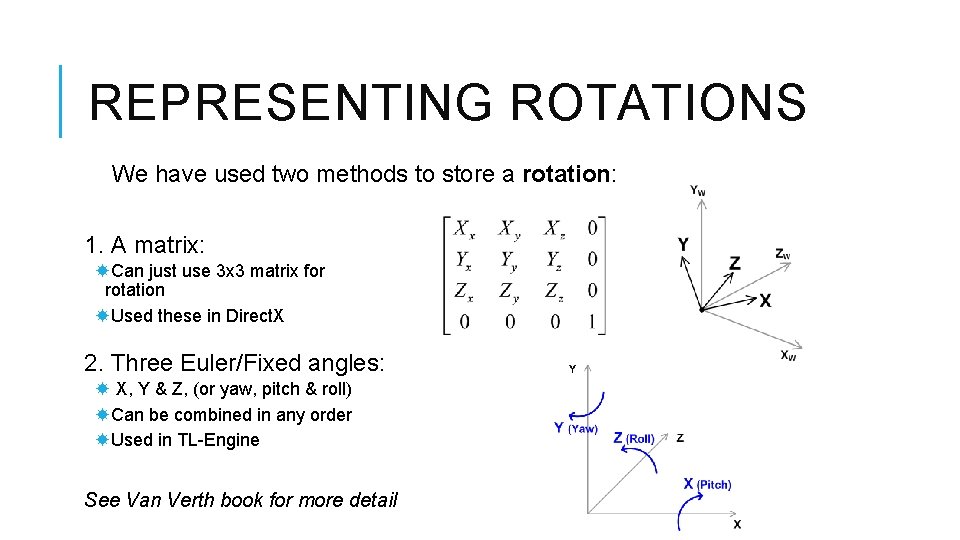
REPRESENTING ROTATIONS We have used two methods to store a rotation: 1. A matrix: Can just use 3 x 3 matrix for rotation Used these in Direct. X 2. Three Euler/Fixed angles: X, Y & Z, (or yaw, pitch & roll) Can be combined in any order Used in TL-Engine See Van Verth book for more detail

CONVERTING BETWEEN FORMATS We can create a matrix from fixed angles Create a rotation matrix for each angle: E. g. Z rotation matrix of α: Multiply the matrices together: M = RX * RY * RZ Different results for different multiplication orders Can also convert matrix back to fixed angles See Van Verth or the matrix class in the labs

EULER ANGLES – PROS/CONS Concise storage – just three floats Euler/Fixed angles seem intuitive But which order to multiply when forming a matrix? Different orders in same app can cause problems Are the rotations world or local rotations? Depends on order again Gimbal lock can occur when one angle is 90° The other angles interfere with each other, result is ambiguous E. g. causing strange spinning effects when looking straight up or down (you will have seen this problem in some games)

MATRICES – PROS/CONS Unambiguous definition of rotation Compared to Euler angles 4 x 4 matrix can also hold position and scale And totally different things: projection matrix Used by graphics hardware Must convert all forms to matrices eventually But uses 16 floats Much processing/storage even for simple operations Can be stored in two ways, by row or by column APIs (Direct. X) and maths texts use different forms

AXIS-ANGLE ROTATIONS Are there other ways to specify rotations? Can specify any rotation as a rotation axis r (a vector) and an angle θ (a scalar): Can convert to and from matrices (see Van Verth or matrix class) Useful way to think about rotation, intuitive But operations are generally complex with this form Including interpolation (see later)

QUATERNIONS Quaternions can be used to represent rotation A general quaternion takes the form: = examinable We will use these forms interchangeably We will mostly consider normalised quaternions: However, several quaternion formulae result in un-normalised quaternions Often need to renormalise quaternions before reuse

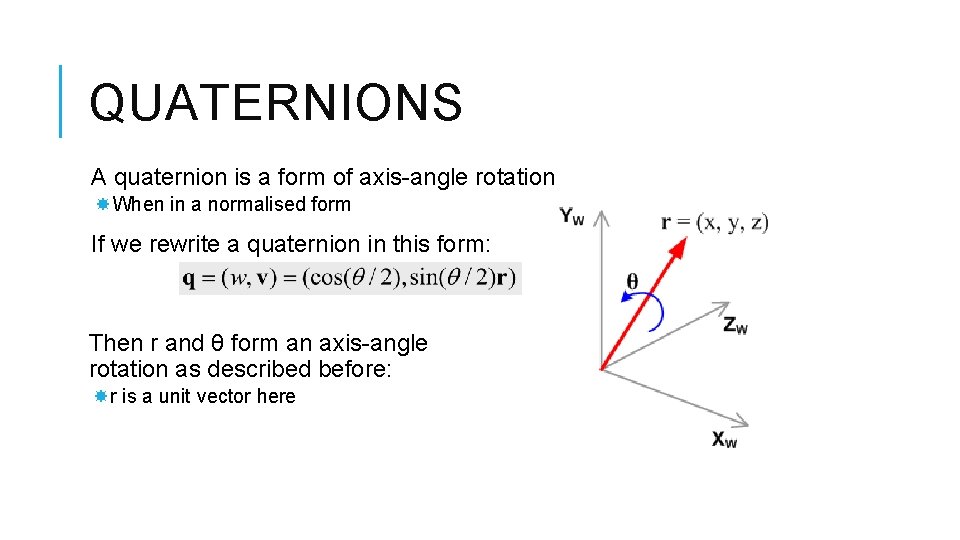
QUATERNIONS A quaternion is a form of axis-angle rotation When in a normalised form If we rewrite a quaternion in this form: Then r and θ form an axis-angle rotation as described before: r is a unit vector here

QUATERNIONS – PROS/CONS Why use this more complex variation on angle-axis form? Because quaternions can easily be: Combined together Used to transform points/vectors Quaternions can be interpolated easily A feature vital for animation, which is more difficult with matrices Quaternions only use 4 floats for storage However, they lack hardware support So we need to convert them to and from matrices

QUATERNION FORMULAE 1 A quaternion can be converted to a matrix: A little expensive, can be simplified in code Transposed from Van Verth book for row-based system (Direct. X / math text difference) Reverse conversion is also possible (see Van Verth) Quaternions don’t convert easily to Euler angles

QUATERNION FORMULAE 2 Quaternions can be added and scaled: Scaling is used for normalisation Two quaternions can be multiplied to create a single quaternion performing both rotations: Same effect as multiplying matrices, order important Coded efficiently this is faster than matrix multiplication N. B. Swapped multiplication order from text for row-based system

QUATERNION FORMULAE 3 Inverse of a quaternion (the rotation in the opposite direction) is simple: Assumes quaternion is normalised Much faster than matrix equivalent, which can be complex We can also represent vectors as quaternions Just set w = 0:

QUATERNION FORMULAE 4 Rotate a vertex or vector p by a quaternion q=(w, v): Slower than matrix equivalent 1 st formula would be reversed for column-based system (2 nd remains same) Derivation of most formulae in Van Verth As well as further detail

QUATERNIONS: INITIAL SUMMARY Quaternions can perform similar operations to matrices With comparable performance But need to convert to / from matrices And can’t store position / scaling No compelling reason to use them yet But next week we will see how quaternions compare to matrices for interpolation And how this is used this for animation It turns out that quaternions are a vital storage method for rotations when animating