Mathmatics for Computer Graphics r A Contents o

Mathmatics for Computer Graphics r A

Contents o o o o Spaces Vectors and Linear combination Affine Combination Coordinate-reference Frames Points and Lines Parametric Representation Linear Transformation Homogeneous Coordinates Mathematics for Computer Graphics

Vector Spaces o A nonempty set V of vectors o Vectors have magnitude and direction. o Addition + Scalar Multiplication · · · u+v = v+u V u+0 = u cu V , (c is scalar) c(u+v) = cu+cv c(du) = (cd)u · (u+v)+w = u+(v+w) · u+(-u) = 0 Directed Line Segments · (c+d)u = cu+du · 1 u = u … but, have no position ! Identical Vectors Mathematics for Computer Graphics

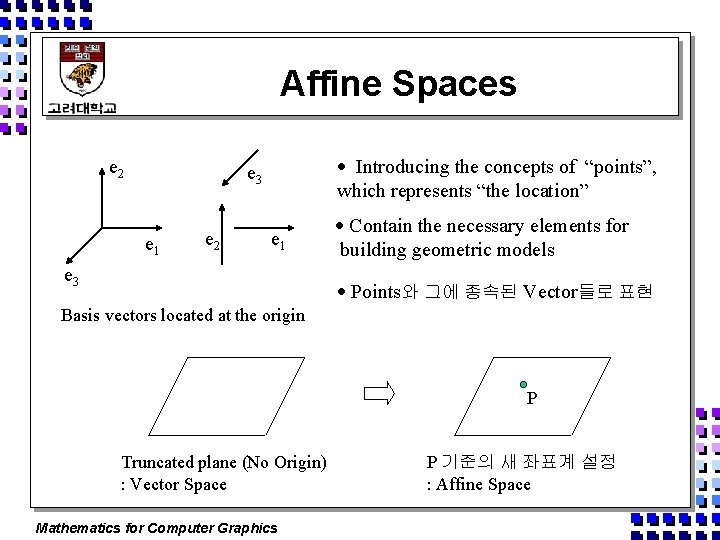
Affine Spaces e 2 Introducing the concepts of “points”, which represents “the location” e 3 e 1 e 2 e 1 e 3 Contain the necessary elements for building geometric models Points와 그에 종속된 Vector들로 표현 Basis vectors located at the origin P Truncated plane (No Origin) : Vector Space Mathematics for Computer Graphics P 기준의 새 좌표계 설정 : Affine Space

Euclidean Spaces o Affine spaces have no concepts of how far apart two points are, or of what the length of a vector is o To Support a measure of distance between points, such as, . . Inner Product! Mathematics for Computer Graphics

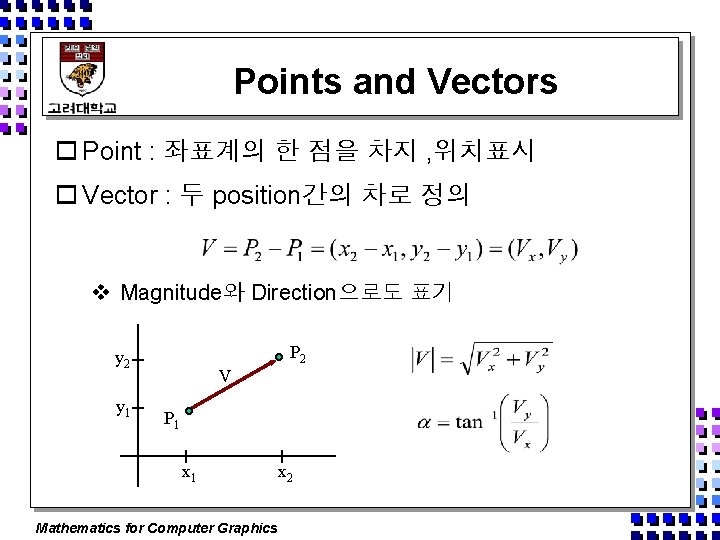
Points and Vectors o Point : 좌표계의 한 점을 차지 , 위치표시 o Vector : 두 position간의 차로 정의 v Magnitude와 Direction으로도 표기 P 2 y 1 V P 1 x 1 Mathematics for Computer Graphics x 2

Vectors (계속) o 3차원에서의 Vector z x o Vector Addition and Scalar Multiplication Mathematics for Computer Graphics V y

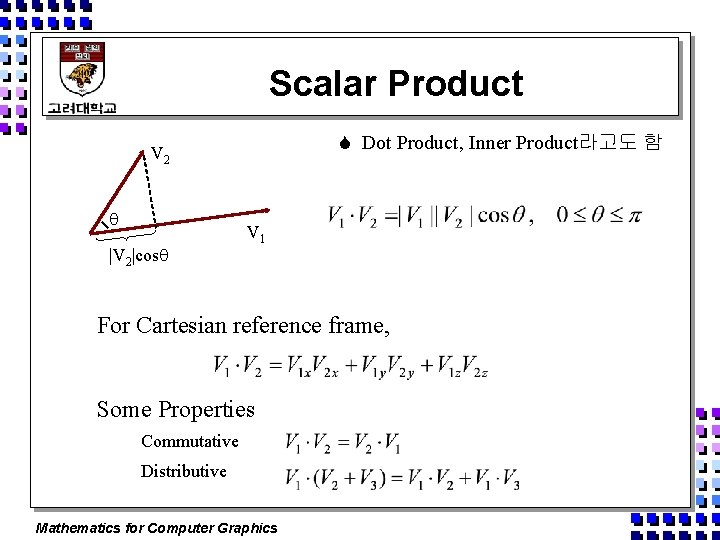
Scalar Product S Dot Product, Inner Product라고도 함 V 2 |V 2|cos V 1 For Cartesian reference frame, Some Properties Commutative Distributive Mathematics for Computer Graphics

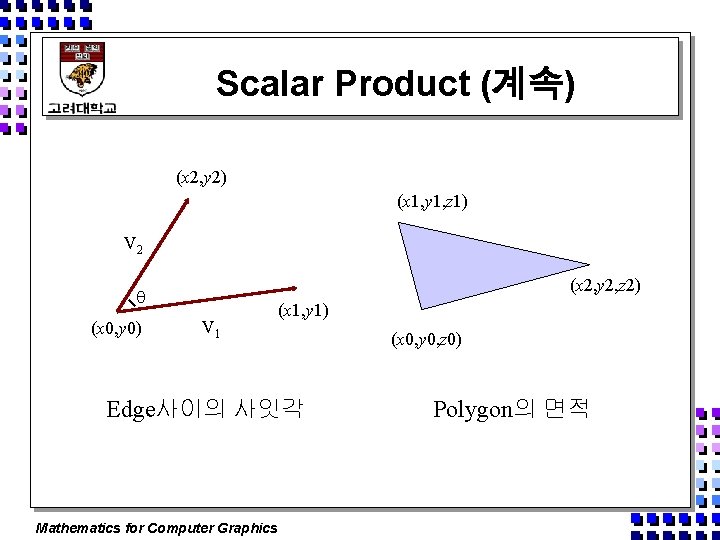
Scalar Product (계속) (x 2, y 2) (x 1, y 1, z 1) V 2 (x 2, y 2, z 2) (x 0, y 0) V 1 (x 1, y 1) Edge사이의 사잇각 Mathematics for Computer Graphics (x 0, y 0, z 0) Polygon의 면적

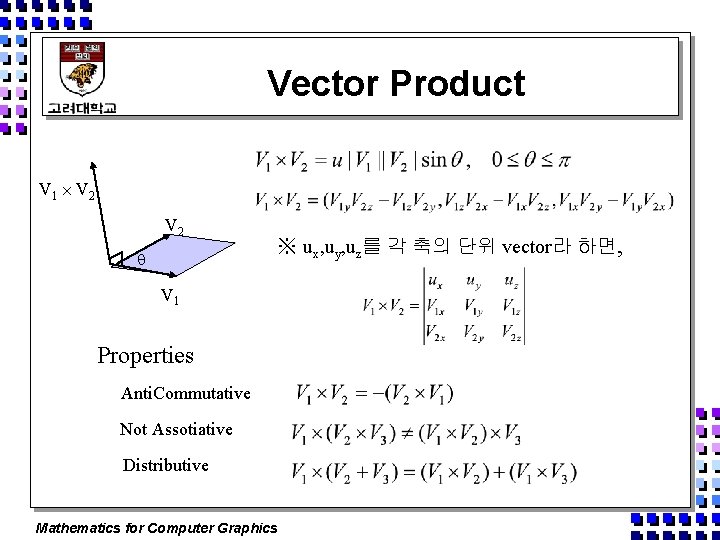
Vector Product V 1 V 2 ※ ux, uy, uz를 각 축의 단위 vector라 하면, V 1 Properties Anti. Commutative Not Assotiative Distributive Mathematics for Computer Graphics

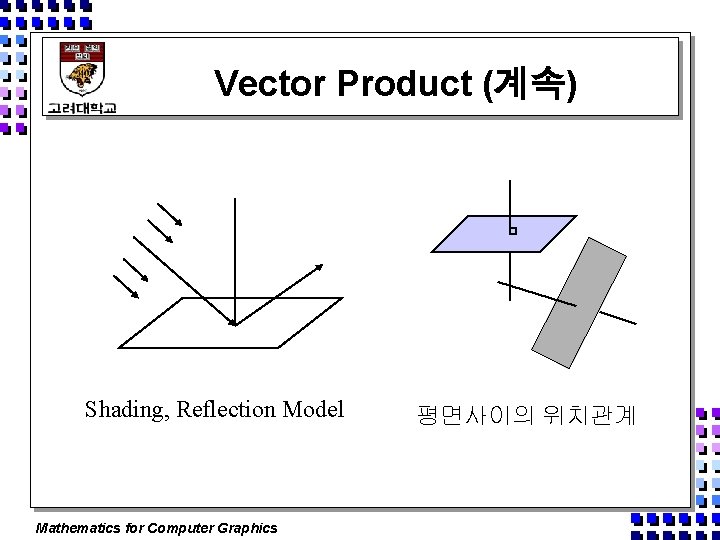
Vector Product (계속) Shading, Reflection Model Mathematics for Computer Graphics 평면사이의 위치관계

Vector Spaces o A nonempty set V of vectors o Addition + Scalar Multiplication · u+v = v+u V · (u+v)+w = u+(v+w) · · · u+(-u) = 0 u+0 = u cu V , (c is scalar) c(u+v) = cu+cv c(du) = (cd)u Mathematics for Computer Graphics · (c+d)u = cu+du · 1 u = u

Linear Combination o Consist of scalar and vectors Ex) Single Vector의 linear combination v v v : real number Mathematics for Computer Graphics : nonnegative

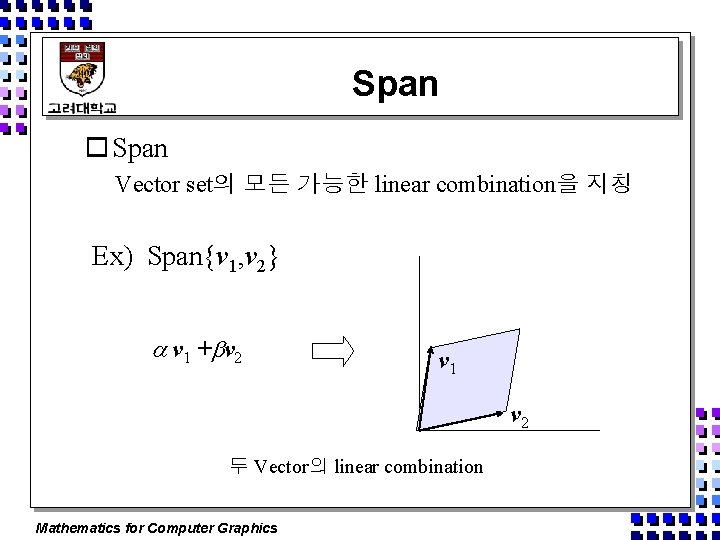
Span o Span Vector set의 모든 가능한 linear combination을 지칭 Ex) Span{v 1, v 2} v 1 + v 2 v 1 v 2 두 Vector의 linear combination Mathematics for Computer Graphics

Linearly Independence A set of vectors B={v 1, …, vp} in V is said to be linearly independent if the vector equation has only the trivial solution c 1=0, …, cp=0. (3, 1) (6, 2) u w v Linearly dependent, w in Span{u, v} Linearly dependent, Collinear (3, 2) w (6, 2) u Linearly independent, Not collinear Mathematics for Computer Graphics v Linearly independent, w not in Span{u, v}

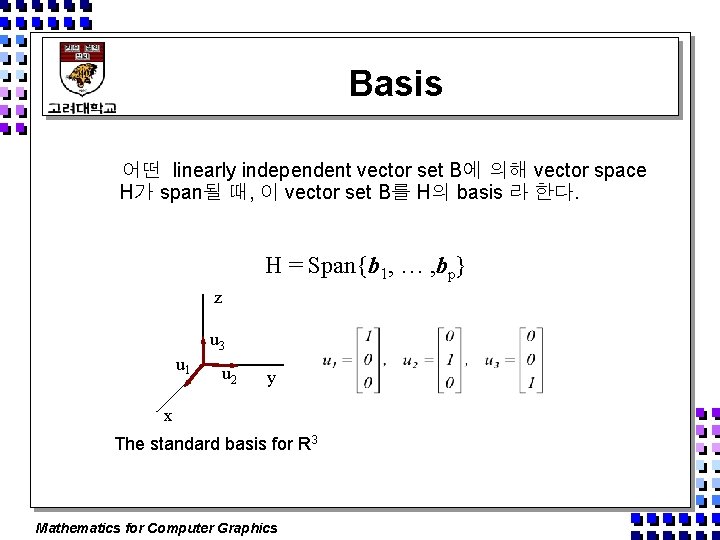
Basis 어떤 linearly independent vector set B에 의해 vector space H가 span될 때, 이 vector set B를 H의 basis 라 한다. H = Span{b 1, … , bp} z u 3 u 1 u 2 y x The standard basis for R 3 Mathematics for Computer Graphics

Orthogonal Basis Orthogonal basis - 각 원소 vector들이 서로 직교 할 때 - for all k for all j k - z u 3 u 1 u 2 y x Orthonormal basis ※ Orthonormal basis 각 원소 vector들이 서로 직교 하면서 동시에 단위 vector로 이루어져 있을 때 Mathematics for Computer Graphics

Affine Space o The Extension of the Vector Space o Geometric operation들이 의미를 갖는 공간 o Points와 그에 종속된 vector들로 표현 P Truncated plane (No Origin) : Vector Space Mathematics for Computer Graphics P 기준의 새 좌표계 설정 : Affine Space

Affine Combination o Linear combination of points in an affine space make no sense (Operations on the points are limited) o Using Parametric Representation Affine combination of two points Line segment joining P 1 and P 2, if 0 t 1 Mathematics for Computer Graphics

Affine Combination Generalized form One Example of Affine Combination gives a point in the triangle. Mathematics for Computer Graphics

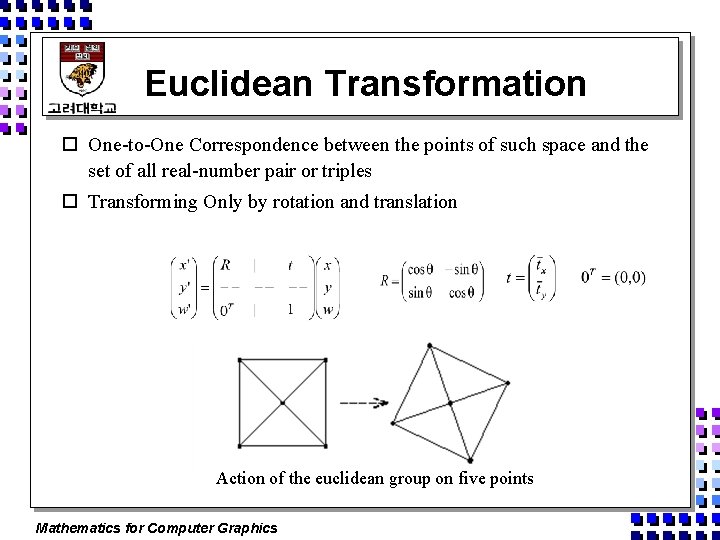
Euclidean Transformation o One-to-One Correspondence between the points of such space and the set of all real-number pair or triples o Transforming Only by rotation and translation Action of the euclidean group on five points Mathematics for Computer Graphics

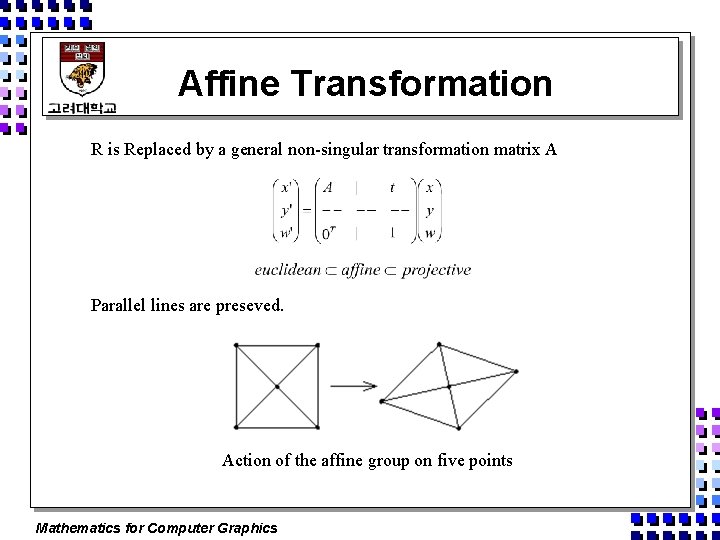
Affine Transformation R is Replaced by a general non-singular transformation matrix A Parallel lines are preseved. Action of the affine group on five points Mathematics for Computer Graphics

General Linear Transformation For general non-singular linear transformations T, We get general linear or projective group of transformations. It preserves the collinearity of points. Action of the projective group on five points Mathematics for Computer Graphics

Coordinate Reference Frames o Coordinate Reference Frames v Cartesian coordinate system x, y, z좌표축사용, 전형적 좌표계 v Non-Cartesian coordinate system – 특수한 경우의 object표현에 사용. – Polar, Spherical, Cylindrical 좌표계등 Mathematics for Computer Graphics

2 D Coordinate System o Two-dimensional Cartesian Reference Frames y x a) Mathematics for Computer Graphics b)

Polar Coordinates v 가장 많이 쓰이는 non-Cartesian System r v Elliptical coordinates, hyperbolic, parabolic plane coordinates등 원 이외에 symmetry를 가진 다른 2차 곡 선들로도 좌표계 표현 가능. Mathematics for Computer Graphics

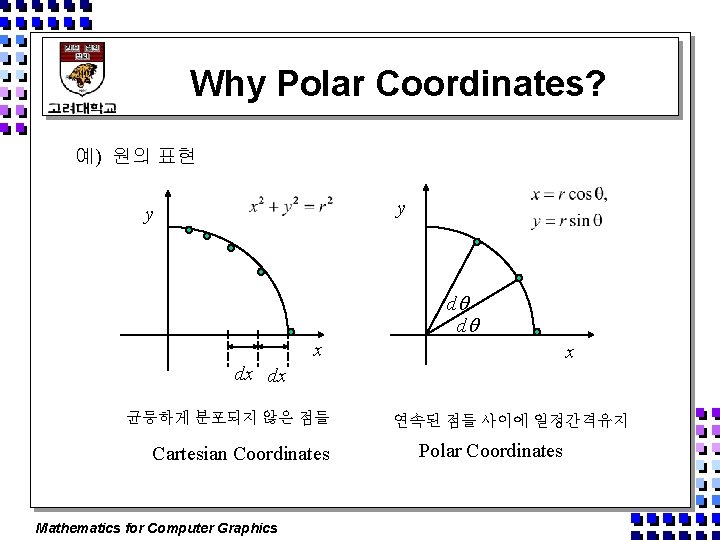
Why Polar Coordinates? 예) 원의 표현 y y d d x x dx dx 균등하게 분포되지 않은 점들 Cartesian Coordinates Mathematics for Computer Graphics 연속된 점들 사이에 일정간격유지 Polar Coordinates

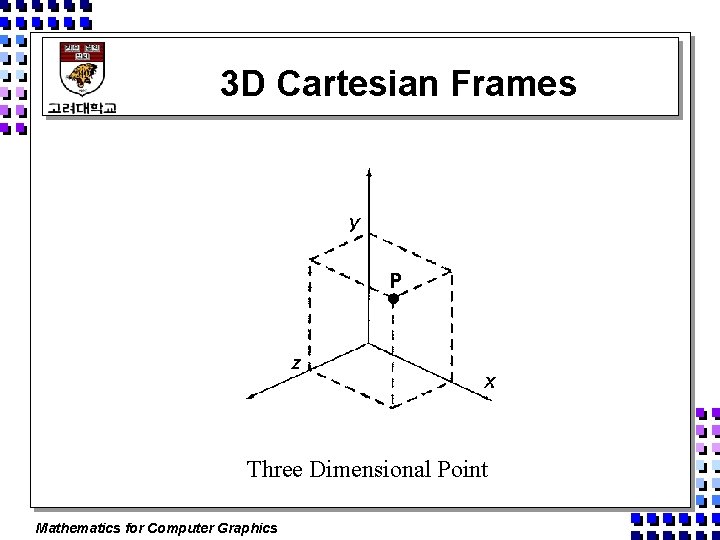
3 D Cartesian Frames Three Dimensional Point Mathematics for Computer Graphics

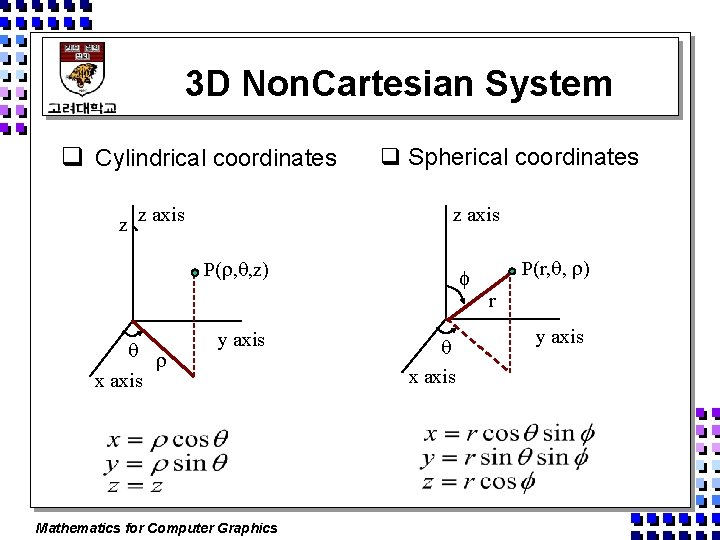
3 D Non. Cartesian System q Cylindrical coordinates q Spherical coordinates z axis z z axis P( , , z) x axis y axis Mathematics for Computer Graphics x axis P(r, , ) r y axis

Points v 가장 기본적인 Output Primitive v 0차원으로 크기와 길이 측정 불가 v 순서쌍(x, y)나 vector형식으로 표기 v Raster Scan display 의 한 Pixel차지 v 2 D or 3 D Mathematics for Computer Graphics

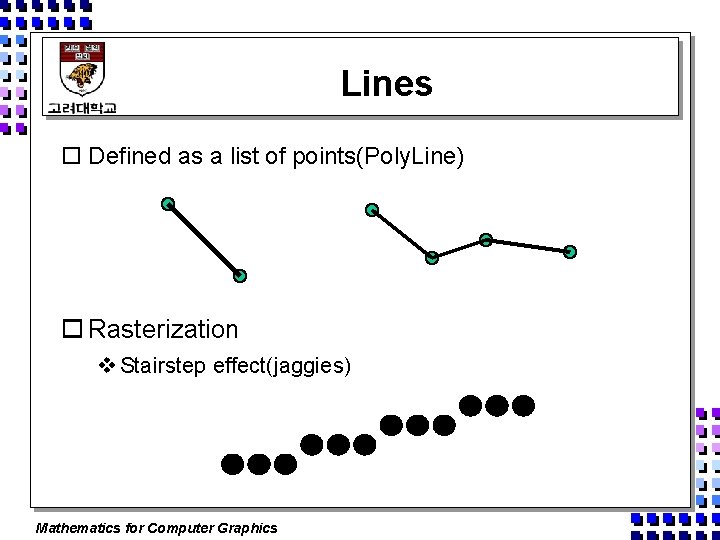
Lines o Defined as a list of points(Poly. Line) o Rasterization v Stairstep effect(jaggies) Mathematics for Computer Graphics

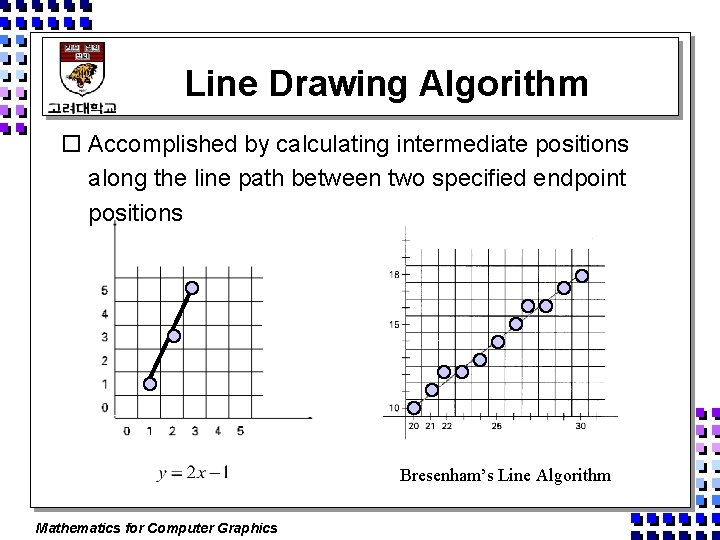
Line Drawing Algorithm o Accomplished by calculating intermediate positions along the line path between two specified endpoint positions Bresenham’s Line Algorithm Mathematics for Computer Graphics

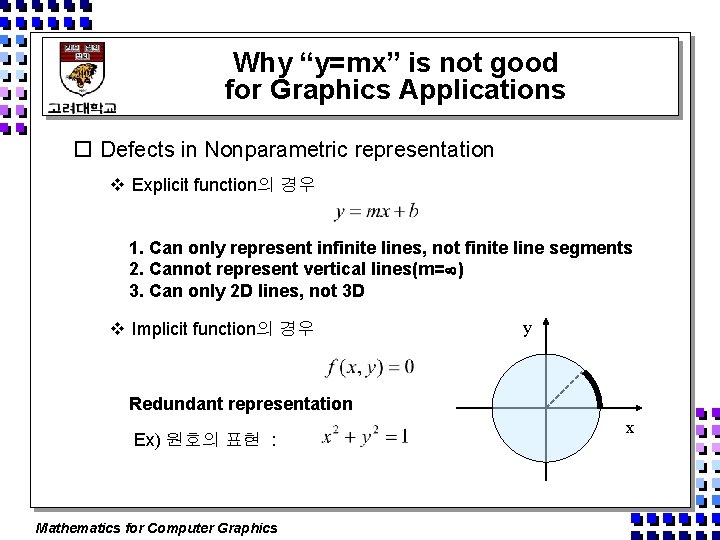
Why “y=mx” is not good for Graphics Applications o Defects in Nonparametric representation v Explicit function의 경우 1. Can only represent infinite lines, not finite line segments 2. Cannot represent vertical lines(m= ) 3. Can only 2 D lines, not 3 D v Implicit function의 경우 y Redundant representation Ex) 원호의 표현 : Mathematics for Computer Graphics x

Parametric Line Equation P 2 p p = P 1 + t * ( P 2 - P 1 ) P 1 x = X 1 + t * ( X 2 - X 1 ) y = Y 1 + t * ( Y 2 -Y 1 ) z = Z 1 + t * ( Z 2 - Z 1 ) Mathematics for Computer Graphics 0. 0 t 1. 0

Parametric Line Equation Can Also be thought of as a blending function. . . P 2 P 1 x = ( 1 - t ) * X 1 + t * X 2 y = ( 1 - t ) * Y 1 + t * Y 2 z = ( 1 - t ) * Z 1 + t * Z 2 Mathematics for Computer Graphics 0. 0 t 1. 0

Linear Blending You can linearly blend any two quantities with : q = Q 1 + t * ( Q 2 - Q 1 ) Or, if you’d prefer : q = ( 1 - t ) * Q 1 + t * Q 2 Color, Shape, Location, Angle, Scale factors, …. Mathematics for Computer Graphics

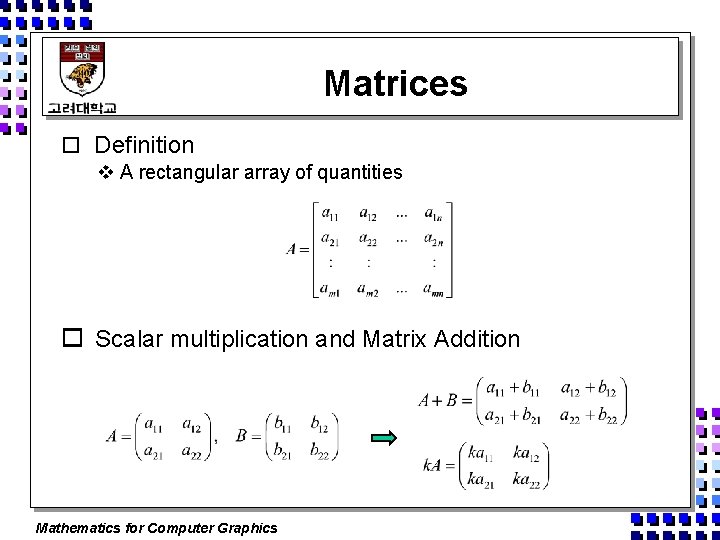
Matrices o Definition v A rectangular array of quantities o Scalar multiplication and Matrix Addition Mathematics for Computer Graphics

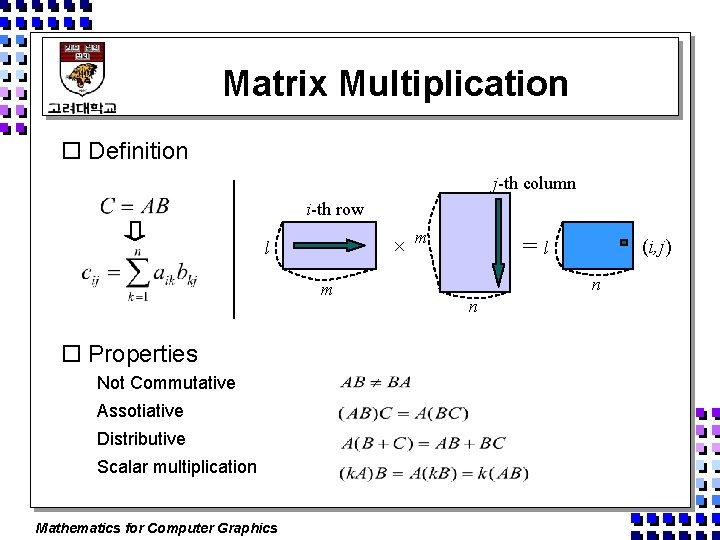
Matrix Multiplication o Definition j-th column i-th row × l m o Properties Not Commutative Assotiative Distributive Scalar multiplication Mathematics for Computer Graphics m = (i, j) l n n

Translation y P x (a) y P’ (b) x Mathematics for Computer Graphics

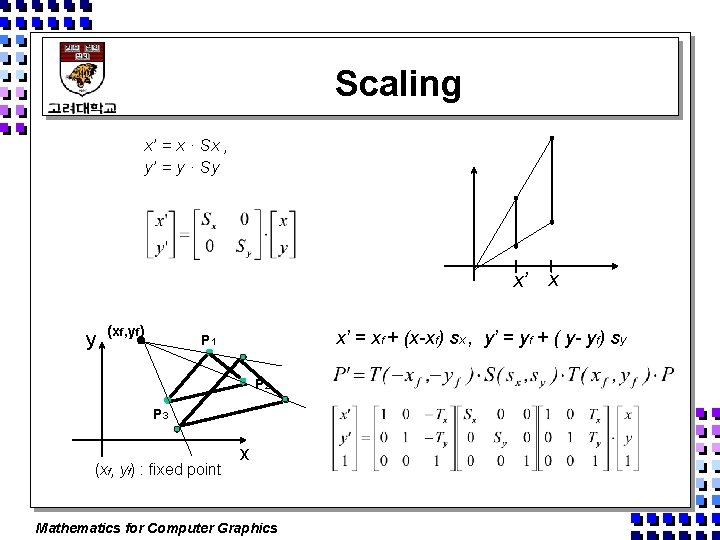
Scaling x’ = x · Sx , y’ = y · Sy x’ y (xf, yf) x’ = xf + (x-xf) sx , y’ = yf + ( y- yf) sy P 1 P 2 P 3 (xf, yf) : fixed point x x Mathematics for Computer Graphics

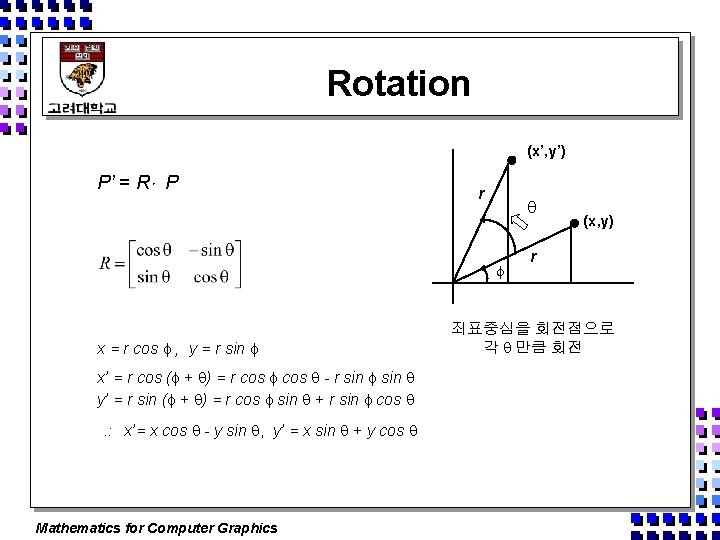
Rotation (x’, y’) P’ = R P r x = r cos , y = r sin x’ = r cos ( + ) = r cos - r sin y’ = r sin ( + ) = r cos sin + r sin cos x’= x cos - y sin , y’ = x sin + y cos Mathematics for Computer Graphics (x, y) r 죄표중심을 회전점으로 각 만큼 회전

Homogeneous Coordinates In basic Transformations, ( Addition ) ( Multiplication ) Only Translation is treated differently We hope to combine the multiplicative and translational terms for two-dimensional geometric transformations into a single matrix representation for enabling the composite transformations such as, Mathematics for Computer Graphics

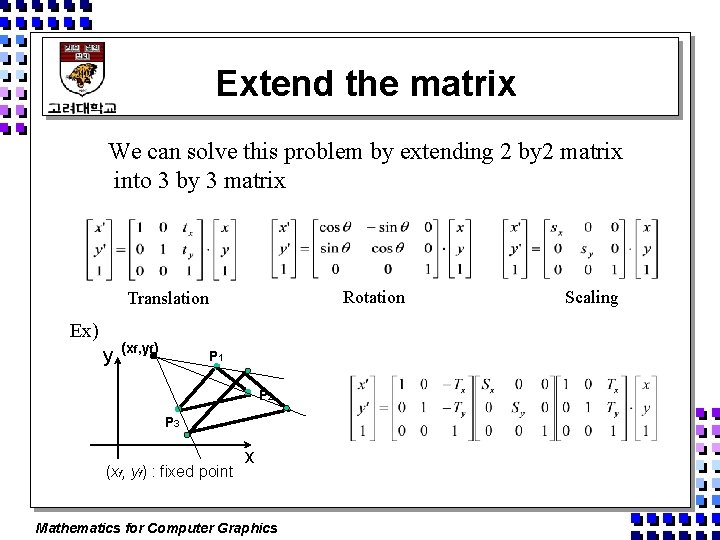
Extend the matrix We can solve this problem by extending 2 by 2 matrix into 3 by 3 matrix Rotation Translation Ex) y (xf, yf) P 1 P 2 P 3 (xf, yf) : fixed point x Mathematics for Computer Graphics Scaling

Homogeneous Space Any two dimensional point can be represented by one of the points along the ray in 3 D space y P(hx 1, hy 1, h) = P(X, Y, h) z =3 P(3 x 1, 3 y 1, 3) z =2 z =1 P(x 1, y 1, 1) P(2 x 1, 2 y 1, 2) 3 D Representarion of homogeneous space Mathematics for Computer Graphics x

Point at Infinity The points with h=0 are called points at infinity, and this will not appear very often. Ex) [ X Y h ] = [ 4 3 1] Mathematics for Computer Graphics

Point at Infinity(Cont’d) Ex) The intersection point of two Parallel lines The resulting homogeneous coordinates [1 -1 0] represent the ‘point of intersection’ for the two parallel lines, i. e. a point at infinity. Mathematics for Computer Graphics

Point at Infinity(Cont’d) B A Two Lines are intersect each other if they are not parallel Non-Homogeneous treatment !! Mathematics for Computer Graphics

Determinant of Matrix o For n 2, the Determinant of n n matrix A is, and for a 2 by 2 matrix, Ex) ※ if A is a triangular matrix, det A is the product of the entries on the main diagonal of A Mathematics for Computer Graphics

Properties of Determinants o Row Operations Let A, B be a square matrix 1) A의 한 행의 실수배가 다른 row에 더해져 B를 만들었다면, det. B = det. A 2) A의 두 행이 교환되어 B를 생성했다면, det. B = -det. A 3) A의 한 행이 k배된 것이 B라면, det. B = k det. A Ex) o Column Operations Mathematics for Computer Graphics

Solving Linear Equations o Linear Equation where, ajk and bj are known o Using Matrix Equation ※Coefficient Matrix A의 역행렬이 존재할 때만 성립 Mathematics for Computer Graphics

Inverse Matrix • Definition • Properties • 2 2 matrix의 경우 If ad-bc = 0, then A is not invertible. Mathematics for Computer Graphics

Inverse Matrix • Algorithm for Finding A-1 : Row reduction [ I A-1] 형태의 row reduction이 존재하지 않으면, A is not invertible. Ex) Mathematics for Computer Graphics

Gaussian Elimination System에서 한 행의 실수배를 다른 행에서 빼어 연립방정식의 차수를 줄여나가다, 한 변수의 해가 구해지면, 역으로 대입해 나머지 변수값을 구한다. • Elementary Row Operation 1. Multiply any row of the augmented matrix by a nonzero constant 2. Add a multiple of one row to a multiple of any other row 3. Interchange the order of any two rows Mathematics for Computer Graphics

Using Row Operation Mathematics for Computer Graphics

Consistency of Linear System 1. Unknown variable의 수에 비해 equation의 수가 적을 때 No Unique solution (Infinite set of solution) 2. Unknown variable의 수에 비해 equation의 수가 많을 때 1) Consistent 한 경우 : 구한 해가 남은 방정식에 대해서도 성립(redundant) 2) Inconsistent한 경우 (infinity) (no solution) Mathematics for Computer Graphics

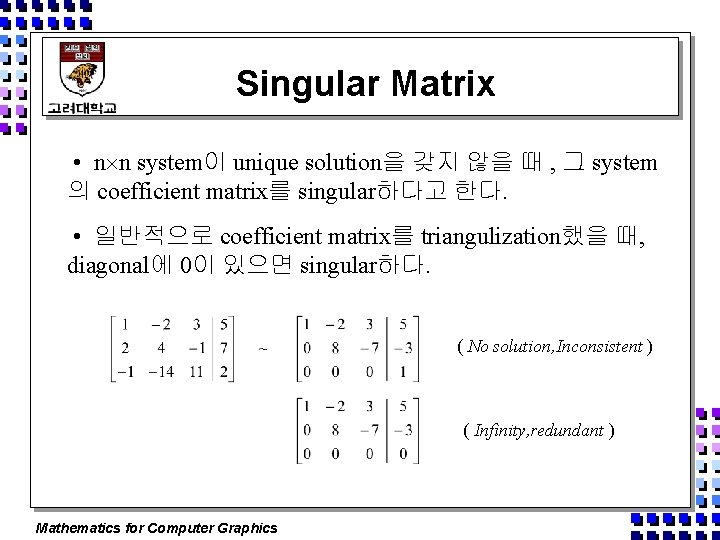
Singular Matrix • n n system이 unique solution을 갖지 않을 때 , 그 system 의 coefficient matrix를 singular하다고 한다. • 일반적으로 coefficient matrix를 triangulization했을 때, diagonal에 0이 있으면 singular하다. ( No solution, Inconsistent ) ( Infinity, redundant ) Mathematics for Computer Graphics

Cramer’s Rule For invertible n n matrix A and b, let Ai(b) be the matrix obtained from A by replacing column i by the vector b, x of Ax=b is, column i Ex) det. A=2 Mathematics for Computer Graphics

Iterative Method - Gaussian Elimination의 roundoff error를 해결하기 위함 - 처음에는 임의의 기대값을 해로 준 다음 error가 최소가 될 때까지 다음 식에 반복 대입 Mathematics for Computer Graphics