Mathematics the language of physics and engineering Professor

Mathematics: the language of physics and engineering Professor Peter Main Maths in the Science Curriculum University of Southampton 29 July 2014 peter. main@iop. org, www. iop. org

Overview l l l Background Mind the Gap SCORE analysis of maths in the sciences Examples of assessment IOP Curriculum Committee Some suggestions for the future

Overview l l l Background Mind the Gap SCORE analysis of maths in the sciences Examples of assessment IOP Curriculum Committee Some suggestions for the future

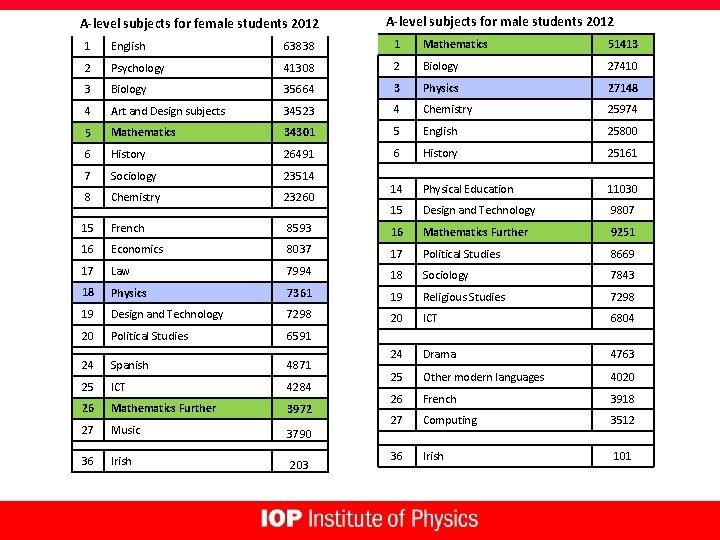
A-level subjects for female students 2012 A-level subjects for male students 2012 1 English 63838 1 Mathematics 51413 2 Psychology 41308 2 Biology 27410 3 Biology 35664 3 Physics 27148 4 Art and Design subjects 34523 4 Chemistry 25974 5 Mathematics 34301 5 English 25800 6 History 26491 6 History 25161 7 Sociology 23514 8 Chemistry 23260 14 Physical Education 11030 15 Design and Technology 9807 15 French 8593 16 Mathematics Further 9251 16 Economics 8037 17 Political Studies 8669 17 Law 7994 18 Sociology 7843 18 Physics 7361 19 Religious Studies 7298 19 Design and Technology 7298 20 ICT 6804 20 Political Studies 6591 24 Spanish 4871 24 Drama 4763 25 ICT 4284 25 Other modern languages 4020 26 Mathematics Further 3972 26 French 3918 27 Music 3790 27 Computing 3512 36 Irish 203 36 Irish 101

Source: Df. E

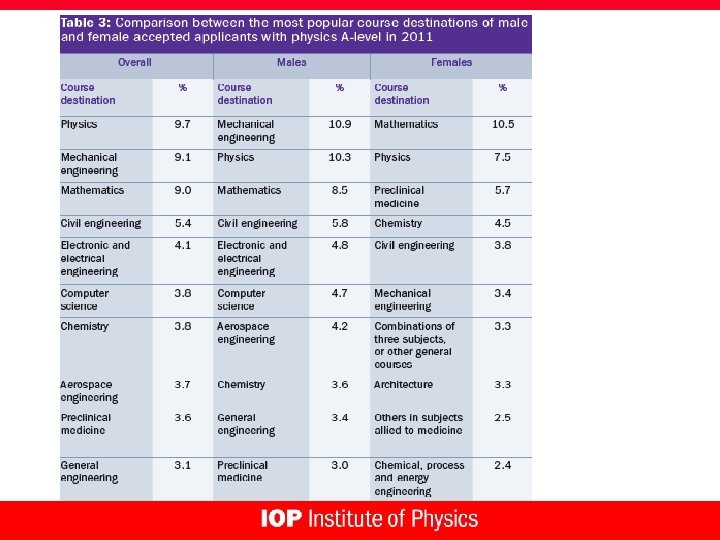
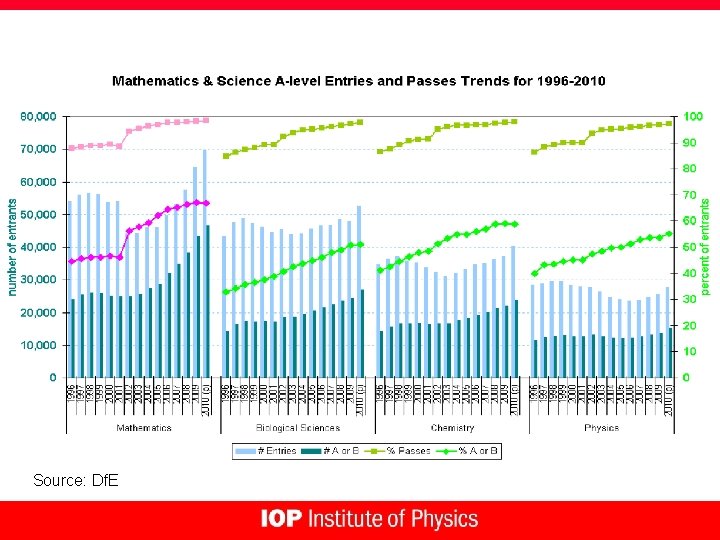
Observations l Grades are rising inexorably l Large increase in numbers that take maths and physics together (now ~86% of physicists take maths) l Essentially all students with A-level physics go to university, the vast majority to use their physics

Overview l l l Background Mind the Gap SCORE analysis of maths in the sciences Examples of assessment IOP Curriculum Committee Some suggestions for the future

Mind the Gap (2011) Rationale: l To understand the extent to which students are prepared to deal with the maths aspects of physics and engineering undergraduate courses l l l Transition from A-Level to degree Reactions to mathematical aspects of degree courses Most and least challenging mathematical aspects Gaps in preparation To understand reasons for not pursuing physics to degree level http: //www. iop. org/publications/iop/2011/page_51934. html

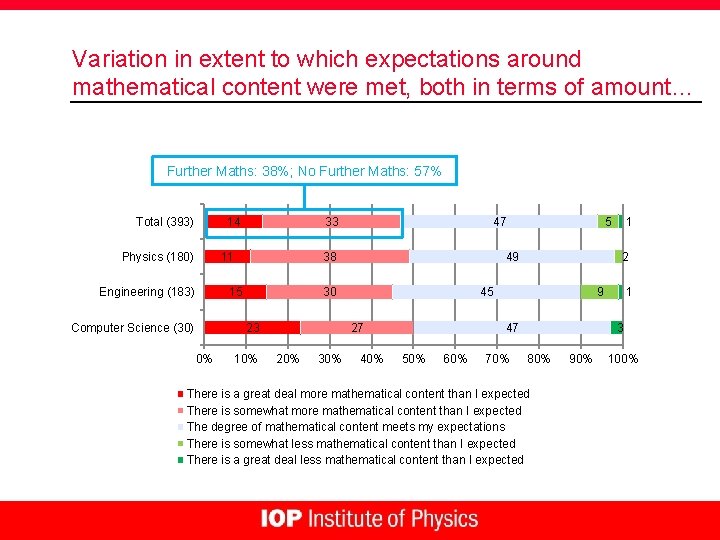
Variation in extent to which expectations around mathematical content were met, both in terms of amount… Further Maths: 38%; No Further Maths: 57% Total (393) 14 Physics (180) 33 11 Engineering (183) 38 15 0% 10% 30% 40% 9 47 50% 60% 1 2 45 27 20% 5 49 30 23 Computer Science (30) 47 70% 1 3 80% There is a great deal more mathematical content than I expected There is somewhat more mathematical content than I expected The degree of mathematical content meets my expectations There is somewhat less mathematical content than I expected There is a great deal less mathematical content than I expected 90% 100%

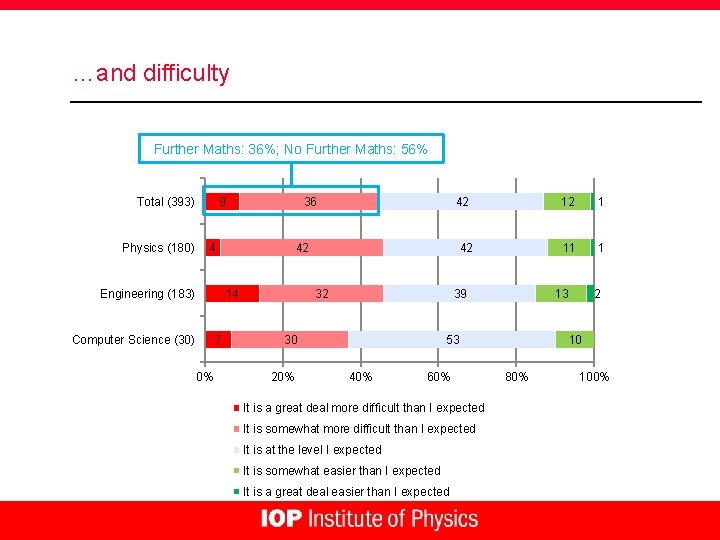
…and difficulty Further Maths: 36%; No Further Maths: 56% Total (393) Physics (180) 9 36 4 42 14 Engineering (183) Computer Science (30) 7 0% 42 42 32 39 30 20% 60% It is a great deal more difficult than I expected It is somewhat more difficult than I expected It is at the level I expected It is somewhat easier than I expected It is a great deal easier than I expected 1 11 1 13 53 40% 12 2 10 80% 100%

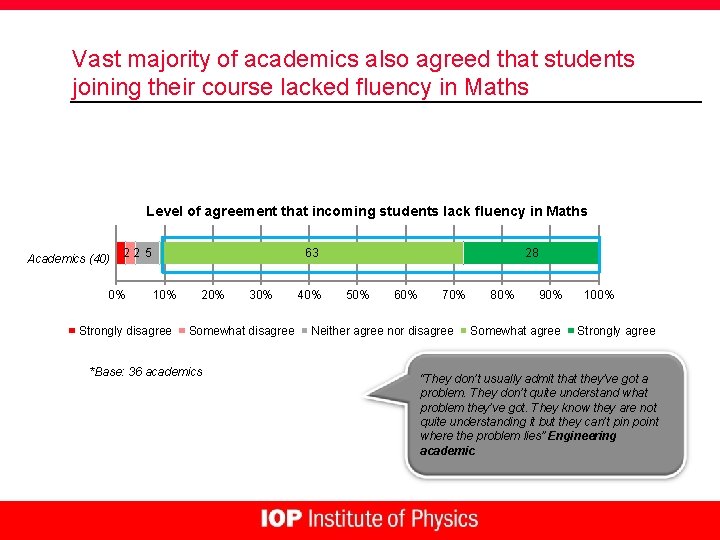
Vast majority of academics also agreed that students joining their course lacked fluency in Maths Level of agreement that incoming students lack fluency in Maths Academics (40) 22 5 0% 63 10% Strongly disagree 20% 30% Somewhat disagree *Base: 36 academics 40% 28 50% 60% 70% Neither agree nor disagree 80% 90% Somewhat agree 100% Strongly agree “They don’t usually admit that they’ve got a problem. They don’t quite understand what problem they’ve got. They know they are not quite understanding it but they can’t pin point where the problem lies” Engineering academic

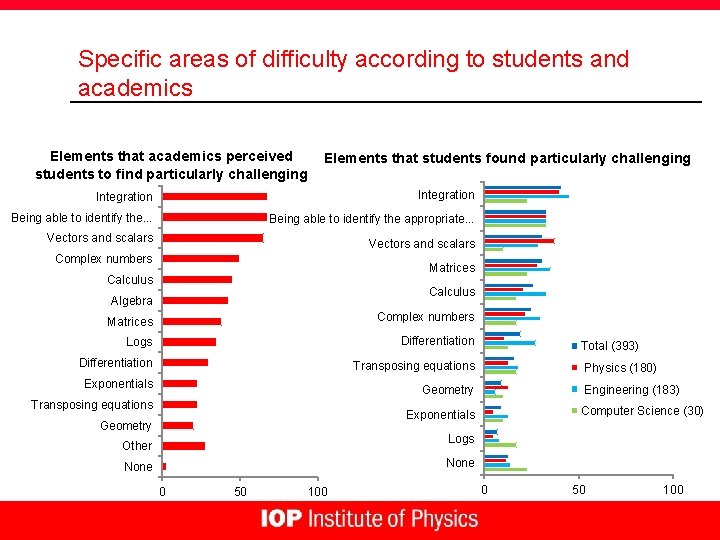
Specific areas of difficulty according to students and academics Elements that academics perceived students to find particularly challenging Elements that students found particularly challenging Integration Being able to identify the. . . Being able to identify the appropriate. . . Vectors and scalars Complex numbers Matrices Calculus Algebra Matrices Complex numbers Logs Differentiation Transposing equations Exponentials Total (393) Physics (180) Engineering (183) Geometry Transposing equations Computer Science (30) Exponentials Geometry Logs Other None 0 50 100

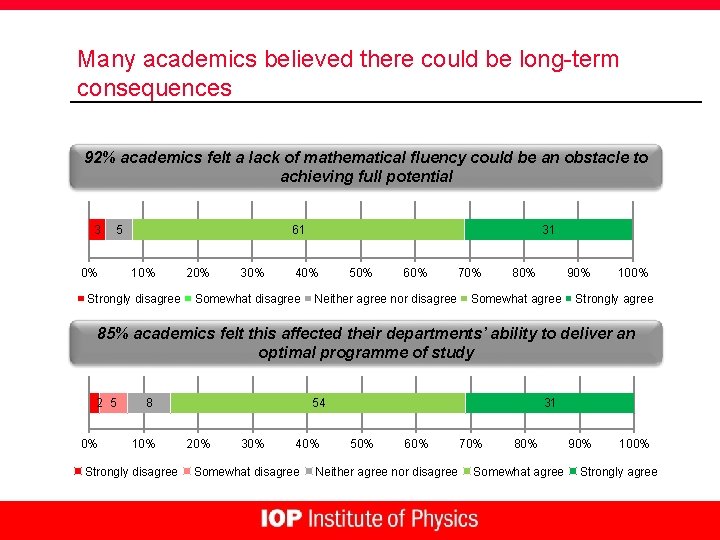
Many academics believed there could be long-term consequences 92% academics felt a lack of mathematical fluency could be an obstacle to achieving full potential 3 5 0% 61 10% Strongly disagree 20% 31 40% Somewhat disagree 50% 60% 70% Neither agree nor disagree 80% 90% Somewhat agree 100% Strongly agree 85% academics felt this affected their departments’ ability to deliver an optimal programme of study 2 5 0% 8 10% Strongly disagree 54 20% 30% 40% Somewhat disagree 31 50% 60% Neither agree nor disagree 70% 80% Somewhat agree 90% 100% Strongly agree

Observations l Despite grades in physics and maths increasing, academics and students do not feel students are well prepared l The lack of mathematical fluency is holding most students back l Some students reported that they did not choose physics because they did not see it as mathematical at A-level

Overview l l l Background Mind the Gap SCORE analysis of maths in the sciences Examples of assessment IOP Curriculum Committee Some suggestions for the future

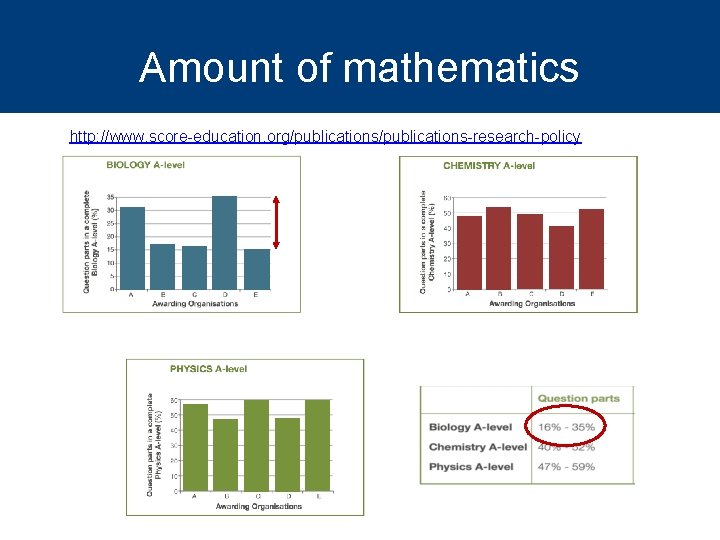
Amount of mathematics http: //www. score-education. org/publications-research-policy

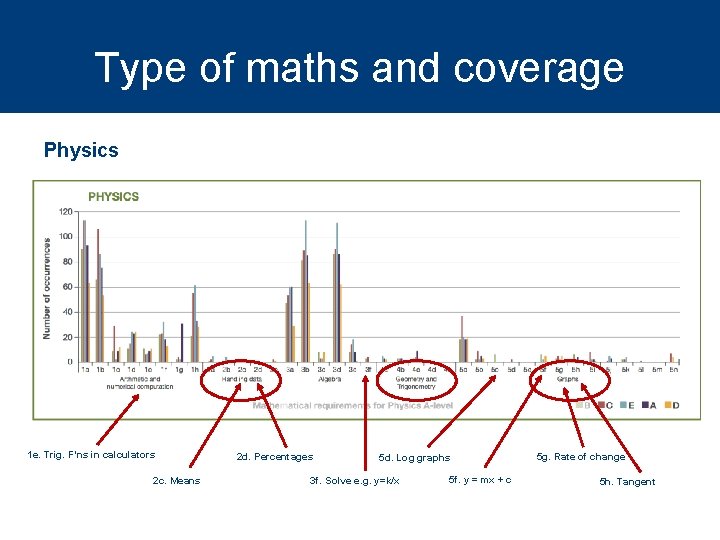
Type of maths and coverage Physics 1 e. Trig. F’ns in calculators 2 c. Means 2 d. Percentages 5 d. Log graphs 3 f. Solve e. g. y=k/x 5 f. y = mx + c 5 g. Rate of change 5 h. Tangent

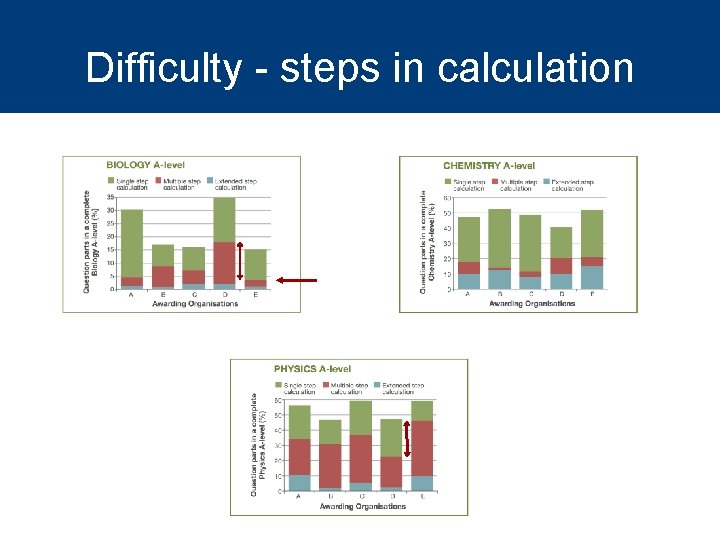
Difficulty - steps in calculation

Observations l Substantial difference between awarding bodies l Parts of stated mathematical requirements of specifications are not examined l Very little in terms of multi-step calculations

Overview l l l Background Mind the Gap SCORE analysis of maths in the sciences Examples of assessment IOP Curriculum Committee Some suggestions for the future

Typical A-level question in 2013

An atypical A-level question 2013 →

Typical question from 1978 l Comparable with harder A-level questions now – note have to set up diagram and write down equation to be solved l This was an O-level question

Typical GCSE question 2013 l l Not only given the formula to use but in a box and in words No physics required to answer question

Overview l l l Background Mind the Gap SCORE analysis of maths in the sciences Examples of assessment IOP Curriculum Committee Some suggestions for the future

IOP Curriculum Committee l Instead of defining physics by content, defining physics by universal themes and competencies l Mathematics includes making estimates and modelling physical situations l Defining the types of assessment, e. g. multiple step

Some of the universal themes l Reductionism The properties of a system can be understood in terms of the “next level down” l l l Universality of physical laws Unification of laws Conservation laws Fields Synthesis Problems can be approached from many different directions l Mathematical formulation Physical laws can be represented in a mathematical form

Some of the competencies l Approximation, taking limiting cases etc. l Simplification Identifying the core elements of a problem l Modelling Developing models of physical systems l Using experiments to test ideas

Overview l l l Background Mind the Gap SCORE analysis of maths in the sciences Examples of assessment IOP Curriculum Committee Some suggestions for the future

Suggestions l Need coherence between A-levels to allow physics to use maths beyond GCSE l 30, 000 students take M and P together: why not have a paired qualification? l It is essential that the assessment of physics A-level is prescribed in terms of mathematical requirements… l …and monitored (by professional bodies? )

Thank you Questions, comments, disagreements…. ? peter. main@iop. org, www. iop. org