Mathematics Teaching in Shanghai UK China Exchange Programme






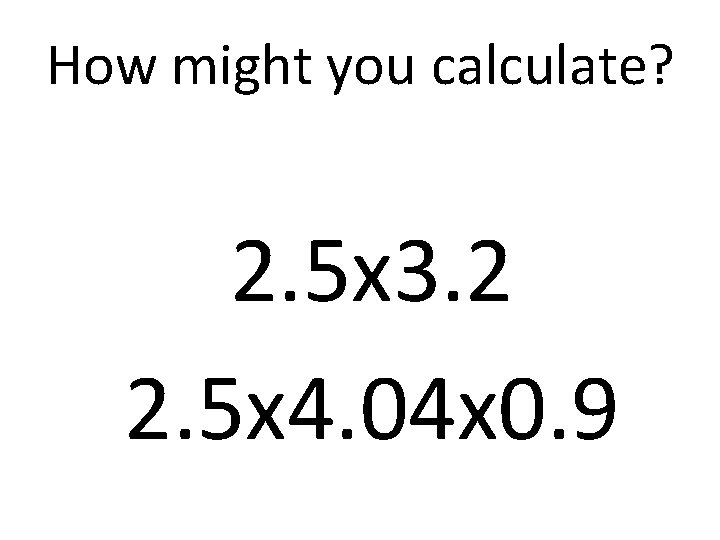



























- Slides: 40

Mathematics Teaching in Shanghai UK China Exchange Programme

Shanghai • A city of 24 million people • High performing in PISA

Characteristics of Shanghai Mathematics Teaching Core beliefs about education (Confucius) High status profession Masters level educated CPD, progression and awards Curriculum content: 20 years of research based policy • Text Book • Homework • • •

Comparison of Curriculum (using text books) Shanghai Y 4 Review and enhancement Multiplying by one digit number Recognition of time(3) Dividing by one digit number Play with geometric shapes Summary and enhancement Review and enhancement Multiplying and dividing Recognition of fraction(1) Calculator Play with geometric shapes Summary and enhancement UK Y 4 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 Numbers and the number System Addition and subtraction Multiplication and division Weight Time Area and perimeter Graphs, tables and charts Carroll and Venn diagrams The number system and properties of number Addition and subtraction Multiplication and division Angles, position and direction Symmetry 2 D and 3 D shapes Length Time Area and perimeter Special numbers Fractions and divisions Ratio and proportion Capacity Time Area and perimeter Graphs, tables and charts Venn and Carroll diagrams

Text Book • • Written by experts and based on research Evolving Progression and review Guidance – How to teach. . – Lesson content • Adapted and refined by schools and then by teams of teachers

Understanding the Basics Basic = deep understanding of number, fluency and flexibility, understanding of structures, mastery of the vocabulary A critical aspect of the approach is a decomposition of each mathematical concept into developmental steps following a Piagetian theory of knowledge based on observation of, and interviews with, students as they attempt to learn a concept.
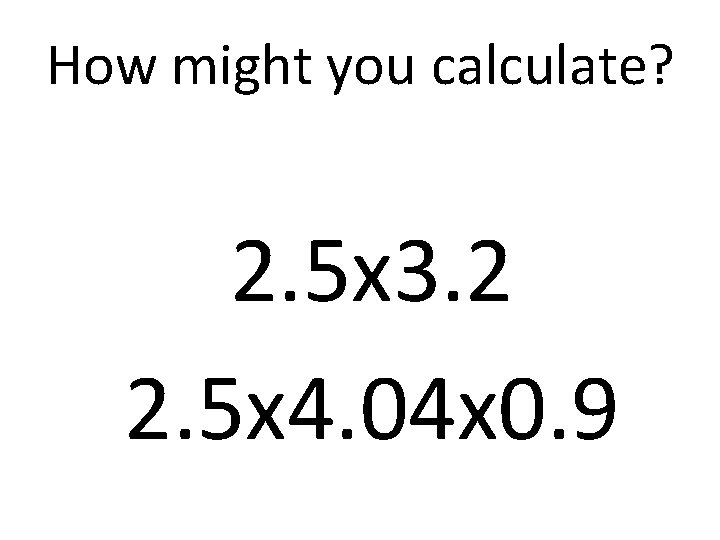
How might you calculate? 2. 5 x 3. 2 2. 5 x 4. 04 x 0. 9

Factorising • 2. 5 x 3. 2 • 3. 2=0. 8 x 4 • 2. 5 x 4=10 • 10 x 0. 8=8 • 2. 5 x 4. 04 x 0. 9?

• 0. 125 x 8 • 0. 5 x 0. 2 • 2. 5 x 4

125 x 80. 8 • 125 x 10. 1 x 8 • 125 x 8 x 10. 1 • 1000 x 10. 1 • 10100

Same Ratio • 240÷ 48 • 60÷ 12 • 20÷ 4

Same Difference String 1 • 122 -92=? • 120 -90=? String 2 • 235 -180=? • 237 -182=? String 3 • 502 -367=? How might you make this calculation easier?

Distributive Law • 3 x 7+4 x 7+3 x 7 • 2 x 19+8 x 19

Lesson Structure • Review the prior linked learning (including models and explanation) e. g. place value • Introduce the concepts and extend the learning through variation teaching – Examples – Contexts – Models and resources – Depth (connections, application, patterns and relationships, explanation) • Practice (meaningful) • Main emphasis is on explanation • Review the lesson

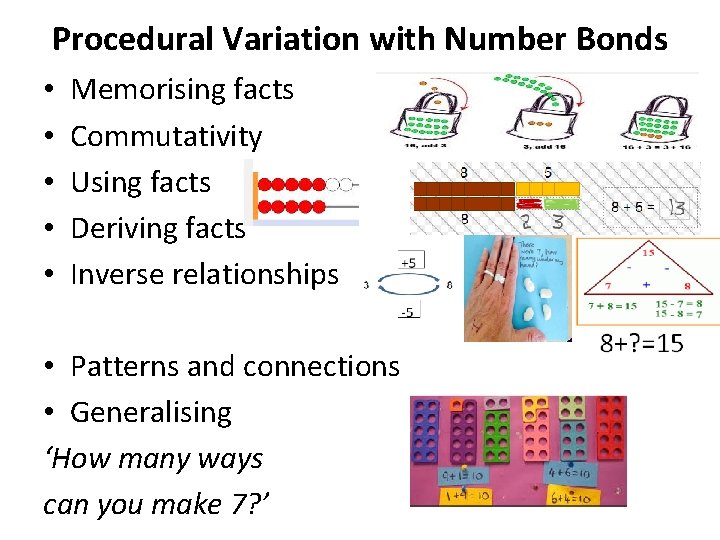
Variation Teaching • Conceptual Variation : the variety of ways into a particular concept • Procedural Variation: what the children should be able to do in relation to a particular concept

Procedural Variation with Number Bonds • • • Memorising facts Commutativity Using facts Deriving facts Inverse relationships • Patterns and connections • Generalising ‘How many ways can you make 7? ’

DEPTH

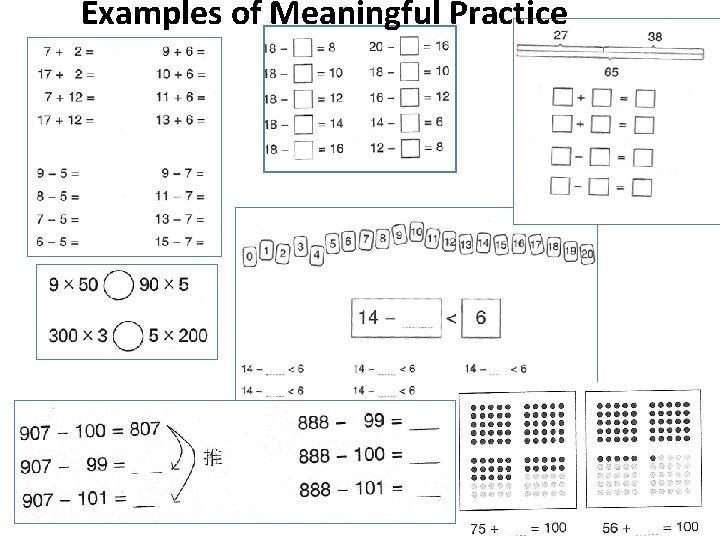
Examples of Meaningful Practice

• Key Point • Critical Point • Difficult Point ‘In our classes mathematical language is very important. Our students must know how to do, say and express maths. ’

Attention to the Mathematics

Repeated addition to multiplication


Only three people in one boat How many 3 s? One three

Only three people in one boat! How many 3 s? Two threes How many children altogether? 3+3=6

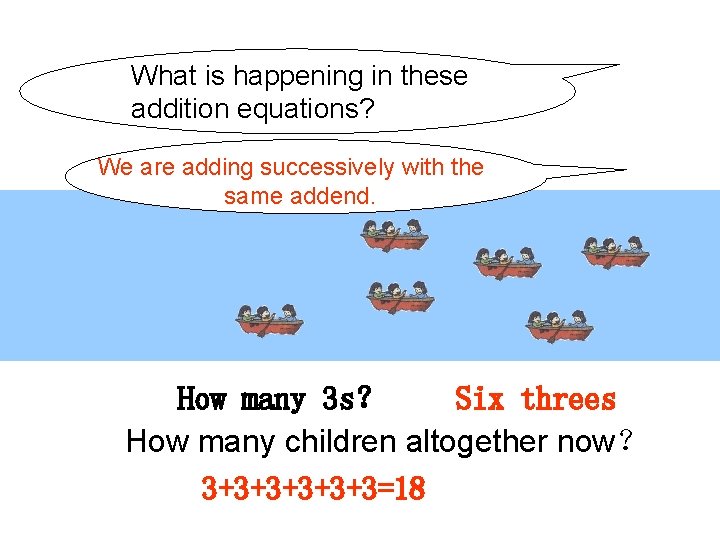
What is happening in these addition equations? We are adding successively with the same addend. Six threes How many 3 s? How many children altogether now? 3+3+3+3=18

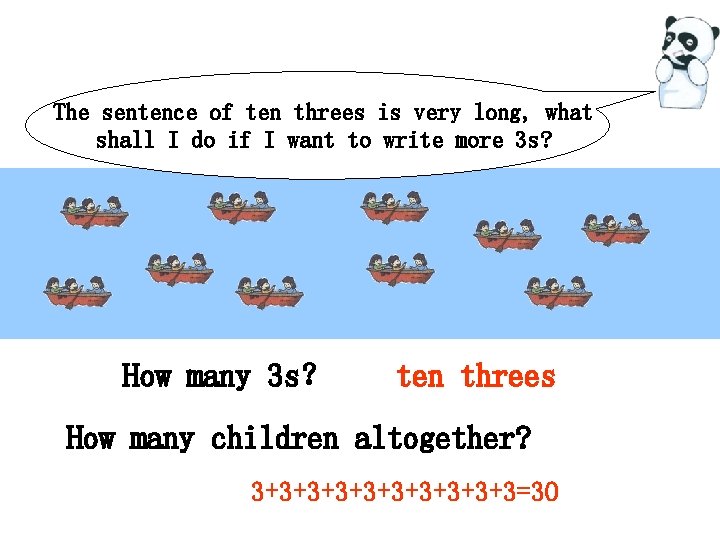
The sentence of ten threes is very long, what shall I do if I want to write more 3 s? How many 3 s? ten threes How many children altogether? 3+3+3+3+3+3=30

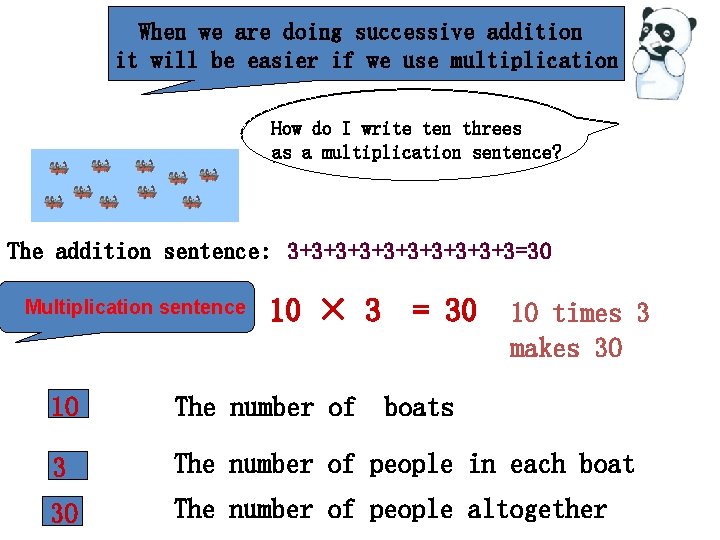
When we are doing successive addition it will be easier if we use multiplication How to. I describe ten threes How do write ten threes as amultiplication? multiplication sentence? in The addition sentence: 3+3+3+3+3+3=30 Multiplication sentence 10 × 3 = 30 10 times 3 makes 30 10 The number of boats 3 The number of people in each boat 30 The number of people altogether

How many children altogether in the cups? 4+4+4=20 (people) Addition number sentence: _________ 5 x 4=20 (people) Mulplication number sentence: _________ How many cups? 5 How many people in each cup? How many people altogether? 4 20

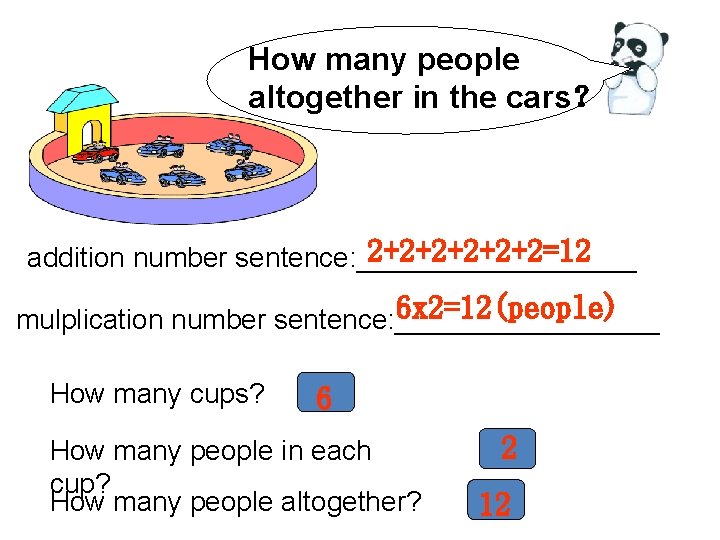
How many people altogether in the cars? 2+2+2+2=12 addition number sentence: _________ 6 x 2=12(people) mulplication number sentence: _________ How many cups? 6 How many people in each cup? How many people altogether? 2 12


Change the following addition sentences into multiplication sentences? 3+3+3= 5+5+5+5= 7+7+7+7+7=

Change these number sentences into multiplication sentences? 5+5+5+5 7+7 = 6 × 5 = 2 × 7 12 -3 -3 = 12 - 4 x 3 2+2+4 = 6 × 2 =2+2+2+2 = 3 × 4 =4+4+4 3+3+3+2+4 =3+3+3 = 5 × 3

The same numbers added successively can be written as multiplication sentences.

What the children do? • Engaged and focused (35 minutes) • Respond in whole class discussion – Suggesting answers – Reasoning and providing proof – Chanting – Precision with language and explanation • Paired and group discussion – Collaborative learning community learning at the same pace (affective: belief, safe)

Review • • Beginning of every term Lesson Teaching sequence End of term ‘What is boring about explanation and review? ’ – Xie Jung, Teacher at Shanghai Experimental Primary School

Beliefs, Values and Ethos • • • Focus versus rest Behaviour Close teacher pupil rapport Belief in depth Belief in learning for everyone ‘If I know I put my hand up and if I don’t know the teacher will explain’ ‘Next time I won’t be wrong’

Collaborative culture in the mathematics team • • • Teacher Research Group Time to reflect Preparation Evaluation Feedback No ego

What can we take?

What can we take? • Can’t wholesale adopt or transplant • Not a good idea to cherry pick policies from other countries • Asian cities look to Western research • We have strengths – Individualistic, independent and free thinking; creative and flexible; respond well to unusual non-routine problems – Problem solving and data handling – TIMMS (year 5) trend is improving… But…

• Subject knowledge development, planning and teaching – Depth and variation – Connections, patterns and relationships – Using resources, models and images effectively – Language, explanation and proof • Beliefs and values – Everyone can do mathematics • Do we have fixed attitudes and approaches? ? – Depth not acceleration – Learning communities • How we use assessment/review • Textbook/meaningful practice