Mathematics Review Exponents Logarithms Series Modular arithmetic Proofs

Mathematics Review • • • Exponents Logarithms Series Modular arithmetic Proofs

• Manipulation of exponents – When the operation involves multiplication, add the exponents algebraically – When the operation involves division, subtract the divisor exponent from the numerator exponent. – When the operation involves powers or roots, multiply the exponent by the power number or divide the exponent by the power number, respectively. – Others

Logarithms • In computer science, all logarithms are to the base 2 unless specified otherwise. • DEFINITION: XA = B if and only if log. XB = A

• THEOREM 1. 1 Proof: Let X = log. CB, Y = log. CA, Z = log. AB. By the definition of logarithms, CX = B, CY = A, and AZ = B Combining these three equalities yields CX = B = AZ = (CY)Z = CYZ Therefore, X = YZ, which implies Z = X/Y, proving theorem.

– THEOREM 1. 2 log. AB = log. A + log. B; A, B > 0 Proof: Let X = log. A, Y = log. B, Z = log. AB. By the definition of logarithms, 2 X = A, 2 Y = B, and 2 Z = AB Combining these three equalities yields 2 X 2 y = 2 x+y= AB = 2 Z Therefore, X+Y = Z, proving theorem. y AB = 2 X 2 = 2 x+y 2 Z = AB

– Some other useful formulas: log (A/B) = log A – log B log (AB) = B log A log X < X for all X > 0

Series • Two usual types – Geometric series: • Such that for a constant g, n=1, 2, … – Mathematical progressions: • Such that for some constant d , n=1, 2, …

– Geometric series • A common one: • Its companion: How to compute it? Let S = , That is, S = A 0 + A 1 + A 2 + … + AN-1 + AN AS = A 1 + A 2 + … + AN-1 + AN +AN+1 AS – S = AN+1 – 1 Therefore, If 0 < A < 1, then Why ?

• For 0 < A < 1 and N tends to , • Another sum that occurs frequently We write S= and multiply by 2, obtaining 2 S = Subtracting these two equations yields S= Thus, S = 2.

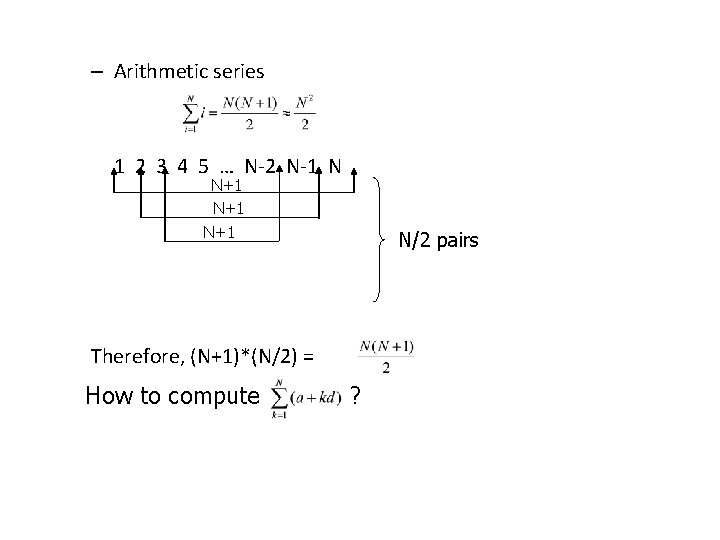
– Arithmetic series 1 2 3 4 5 … N-2 N-1 N N+1 N+1 N/2 pairs Therefore, (N+1)*(N/2) = How to compute ?

– Harmonic series For positive integers N , the N th harmonic number is HN = = – Other formulas

• Modular Arithmetic – A is congruent to B modulo N, written A B (mod N), if N divides A-B. – Intuitively, this means that the remainder is the same when either A or B is divided by N. – Ex’s, • Check the following – – 20 ? 6 (mod 2) 25 ? 10 (mod 3) 20 ? 6 (mod 4) 100 ? 23 (mod 6)

– If A B (mod N), then A+C B+C (mod N) AD BD (mod N) (A+C) – (B+C) = A – B Since A B (mod N), from the definition, N divides A-B. Thus, N divides (A+C)-(B+C) Therefore, A+C B+C (mod N) Since A B (mod N), based on the definition, there exists an integer k such that A-B = k N. Now, AD-BD = (A-B)D = k ND So, N divides AD-BD. Therefore, AD BD (mod N)

• Proofs – Two most common ways of proving statements in data structure analysis: proof by induction and proof by contradiction. – The best way of proving that a theorem is false is by exhibiting a counterexample.

• Proof by induction (two steps) – Base case: Establish that a theorem is true for some small value(s). This step is almost always trivial. – Induction step: • An inductive hypothesis is assumed (which means that theorem is assumed to be true for all cases up to some limit k) • Using this assumption, theorem is then shown to be true for the next value, which is typically k+1.

– Example 1: Fibonacci numbers Fi < (5/3)i, for i >=1 Fibonacci numbers: F 0 = 1, F 1 = 1, F 2 = 2, …, Fi = Fi-1 + Fi-2 Base case: verify that theorem is true for the trivial cases. F 1 = 1 < 5/3 F 2 = 2 < 25/9 Inductive hypothesis: We assume that theorem is true for i = 1, 2, …, k. To prove theorem, we need to show that Fk+1 < (5/3)k+1 We have Fk+1 = Fk + Fk-1 < (5/3)k+ (5/3)k-1 (using inductive hypothesis) = (3/5) (5/3)k+1 + (3/5)2(5/3)k+1 = (3/5) (5/3)k+1 + (9/25)(5/3)k+1 = (3/5 + 9/25) (5/3)k+1 = (24/25) (5/3)k+1 < (5/3)k+1 which proves theorem.

– Example 2: THEOREM 1. 3 If N >= 1, then Proof: The proof is by induction. Base case: Obviously, theorem is true when N = 1 Inductive hypothesis: Assume that theorem is true for 1 <= k <= N. We need to establish that, under this assumption, theorem is true for N+1. We have Applying the inductive hypothesis, we obtain = (N+2)(2 N+3) Thus,

– Proof by contradiction • Strategies: – Assume that theorem is false – Show that this assumption implies that some know property is false, which indicates the original assumption was wrong. • Example 1: The number of primes is infinite. A positive integer number is a prime if and only if only 1 and itself divide the number. Proof: We assume that there is a finite number of primes, so that there is some largest prime Pk. Let P 1, P 2, …, Pk be all the primes in order and consider N = P 1 P 2 … Pk + 1 Clearly, N > Pk, so by assumption N is not prime. However, none of P 1, P 2, …, Pk divides N exactly. This is a contradiction, because every number is either prime or a product of primes. Hence, the original assumption is false, which implies that theorem is true.

Example 1 • is not a rational number. – Note: a rational number can be represented by a irreducible fraction of two integers • Proof. By contradiction – (Who can do this? )

– Proof by counterexample • Proof by counterexample is usually used to prove that a theorem is false. • Constructing a counterexample is not as easy as it seems • Example 1: The statement Fibonacci number Fk <= k 2 is false. • Proof: F 11 = 144 > 112. Therefore, the statement is false.

A Brief Introduction to Recursion • A function is recursive if itself is used in its definition. • A recursive function must have a base (base cases) and a general relation which reduces a general case to simple case, and eventually to the base (or base cases). • Ex’s?

• A good way to understand recursion is through building a recursion tree • The good points for recursion are – To write elegant codes – Easier analysis of the algorithm performance • The bad points are – Time consuming (Why? ) – Space consuming (Why? )

Four Basic Rules of Recursion • Base cases: You must always have some base cases, which can be solved without recursion. • Making progress: For cases that are to be solved recursively, the recursive call must be always be to a case that makes progress toward a base case. • Design rule. Assume that all the recursive calls work. • Compound interest rule. Never duplicate work by solving the same instance of a problem in separate recursive calls.