Mathematics N 2 Module 1 Exponents and logarithms


















- Slides: 21

Mathematics N 2

Module 1: Exponents and logarithms www. futuremanagers. com

Module 1: Exponents and logarithms (continued) www. futuremanagers. com

Module 2: Factorisation, HCF, LCM and algebraic fractions www. futuremanagers. com

Module 2: Highest common factor and lowest common multiple (continued) HIGHEST COMMON FACTOR AND LOWEST COMMON MULTIPLE The highest common factor (HCF) of two or more numbers is the common factor of all those numbers with the greatest value. The lowest common multiple (LCM) of two or more numbers is the smallest possible number into which all the numbers can be divided exactly. www. futuremanagers. com

Module 2: Highest common factor and lowest common multiple (continued) www. futuremanagers. com

Module 3: Equations, word problems and manipulation of technical formulae LINEAR EQUATIONS A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and (the first power of) a single variable. The power of the highest variable is 1. Linear equations could have one or more variables. www. futuremanagers. com

Module 3: Equations, word problems and manipulation of technical formulae (continued) www. futuremanagers. com

Module 3: Equations, word problems and manipulation of technical formulae (continued) www. futuremanagers. com

Module 3: Equations, word problems and manipulation of technical formulae (continued) WORD PROBLEMS When an answer is needed to a mathematical problem that is described in words as well as numbers, it is called a word problem. You find the solution by setting up an equation that represents the problem, and then solve it. www. futuremanagers. com

Module 3: Equations, word problems and manipulation of technical formulae (continued) MANIPULATION OF TECHNICAL FORMULAE Manipulation of technical formula can also be described as changing the subject of the formula. An equation can be manipulated in such a way that the required variable is isolated on the left-hand-side, and everything else is written on the right-hand -side. This manipulation is described as making the wanted variable the subject of the formula. www. futuremanagers. com

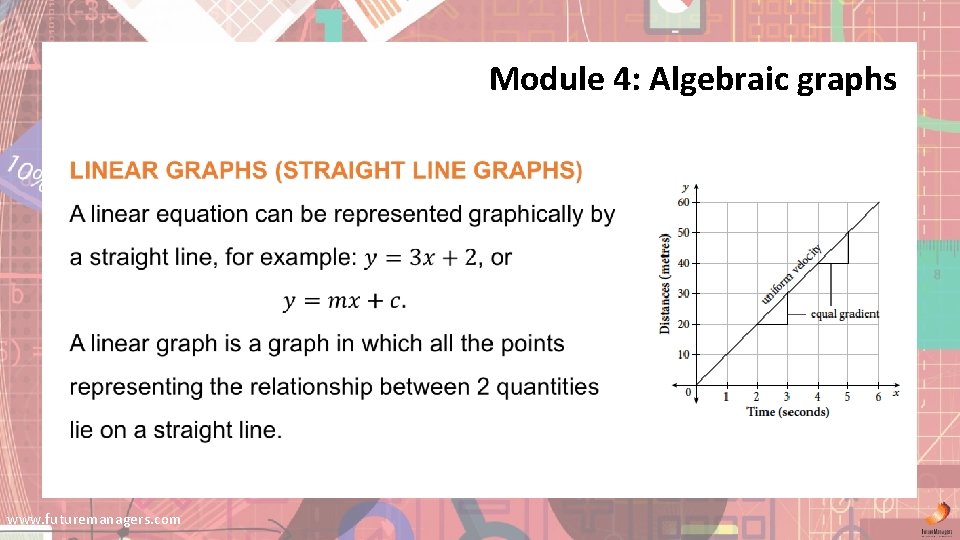
Module 4: Algebraic graphs www. futuremanagers. com

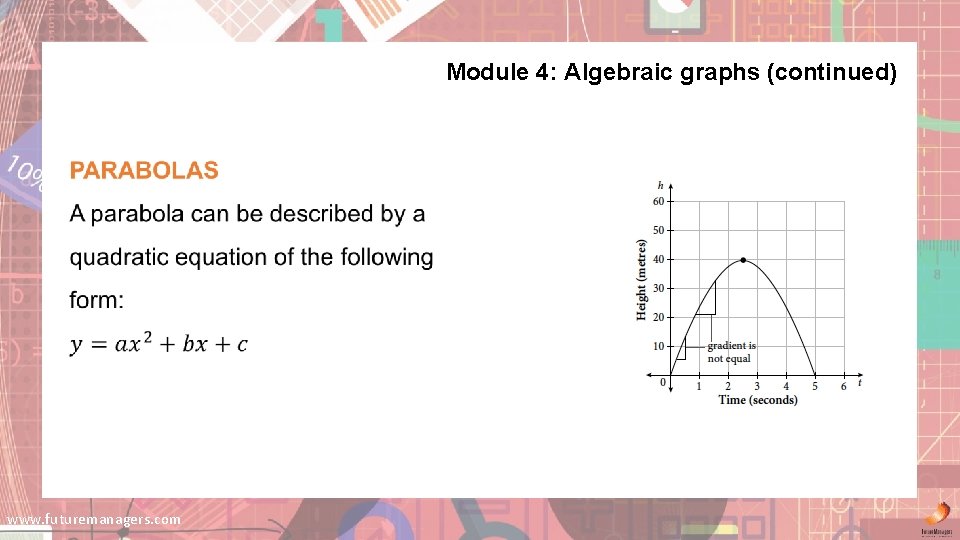
Module 4: Algebraic graphs (continued) www. futuremanagers. com

Module 4: Algebraic graphs (continued) GRAPHICAL SOLUTIONS OF SIMULTANEOUS EQUATIONS Simultaneous equations can be solved exactly using an algebraic method or approximately using the graphical method. The first step is to draw the graphs and then read the coordinates of the points where the two graphs cut each other. These points are the solutions and are called the points of intersection of the graphs. www. futuremanagers. com

Module 5: Measuring of angles, angular and peripheral velocity and sectors of circles MEASURING OF ANGLES There are several ways to measure the size of an angle. One way is to use the unit degrees. A 360° angle is a full rotation or a full circle. This is called one revolution. www. futuremanagers. com

Module 5: Measuring of angles, angular and peripheral velocity and sectors of circles (continued) RADIANS Radians are used as an alternative way of measuring angles, or the amount of turn. A radian is defined as the angle made at the centre of a circle between two radii when the arc length on the circumference between the two radii (radiuses) is equal to the length of one radius. www. futuremanagers. com

Module 5: Measuring of angles, angular and peripheral velocity and sectors of circles (continued) www. futuremanagers. com

Module 5: Measuring of angles, angular and peripheral velocity and sectors of circles (continued) www. futuremanagers. com

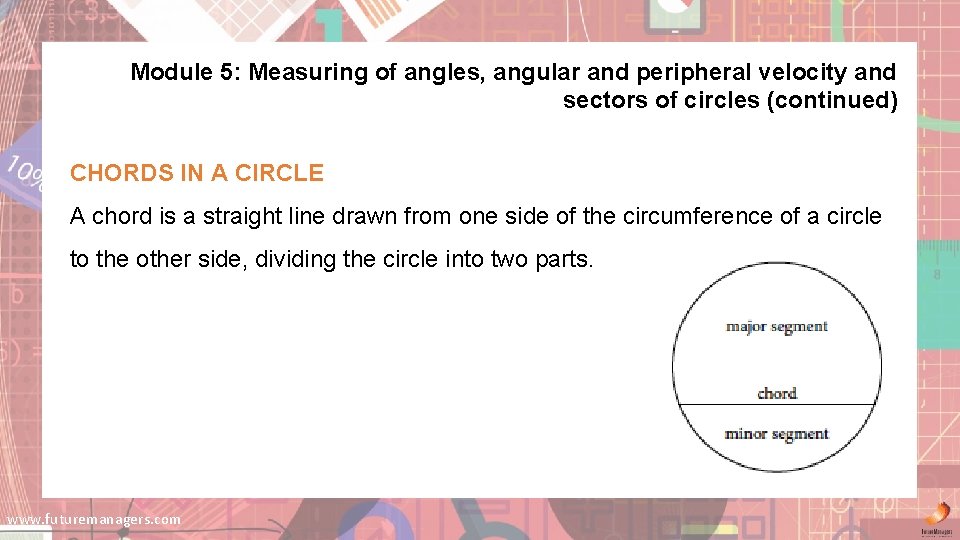
Module 5: Measuring of angles, angular and peripheral velocity and sectors of circles (continued) CHORDS IN A CIRCLE A chord is a straight line drawn from one side of the circumference of a circle to the other side, dividing the circle into two parts. www. futuremanagers. com

Module 6: Trigonometry www. futuremanagers. com

Module 7: Mensuration MENSURATION When calculating equations which have different units of measurement, we need to remember: • Perimeter: The total distance around a shape; • Circumference: The total distance around a circle; • Area: The total amount of surface space occupied by a shape; • Surface area: The total outside area of a shape; and • Volume: The total amount of space a shape occupies. www. futuremanagers. com