Mathematics Is The Collection of All Possible Patterns

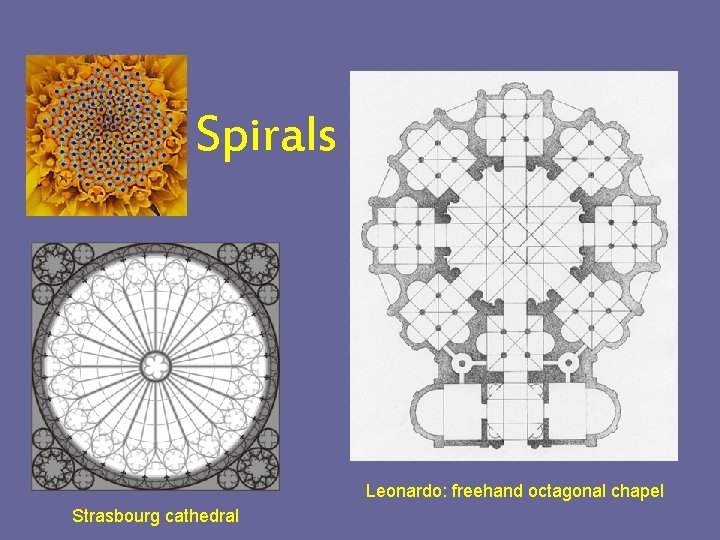
Spirals Leonardo: freehand octagonal chapel Strasbourg cathedral

Complexity that is neither too simple nor to difficult Complexity with reductionism is science Complexity without reductionism is art Art is I. Science is We’

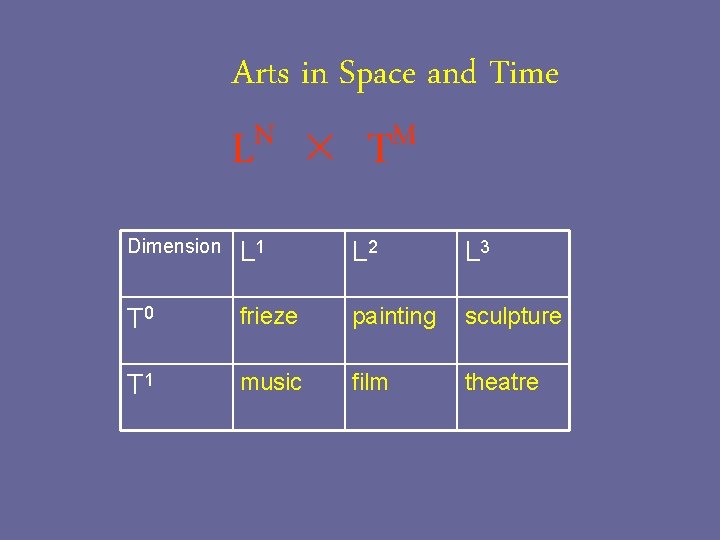
Arts in Space and Time N L M T Dimension L 1 L 2 L 3 T 0 frieze painting sculpture T 1 music film theatre

Four-dimensional geometry Charles Hinton The Fourth Dimension, (1904) Salvador Dali, Corpus Hypercubus, (1954)

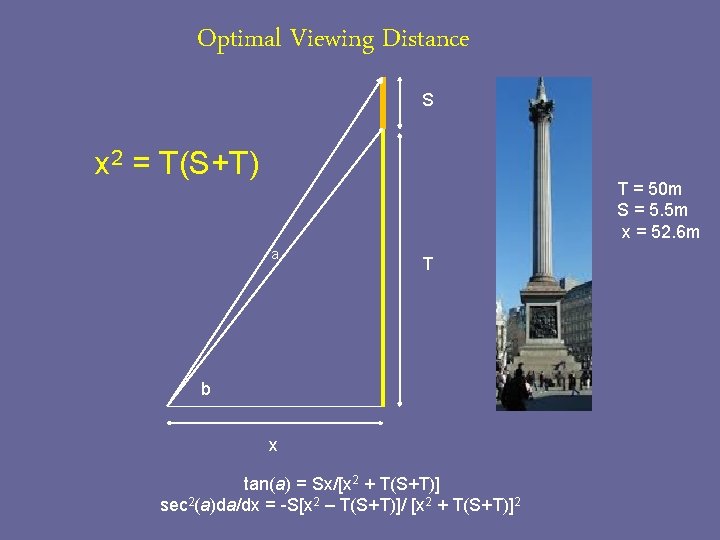
Optimal Viewing Distance S x 2 = T(S+T) T = 50 m S = 5. 5 m x = 52. 6 m a T b x tan(a) = Sx/[x 2 + T(S+T)] sec 2(a)da/dx = -S[x 2 – T(S+T)]/ [x 2 + T(S+T)]2

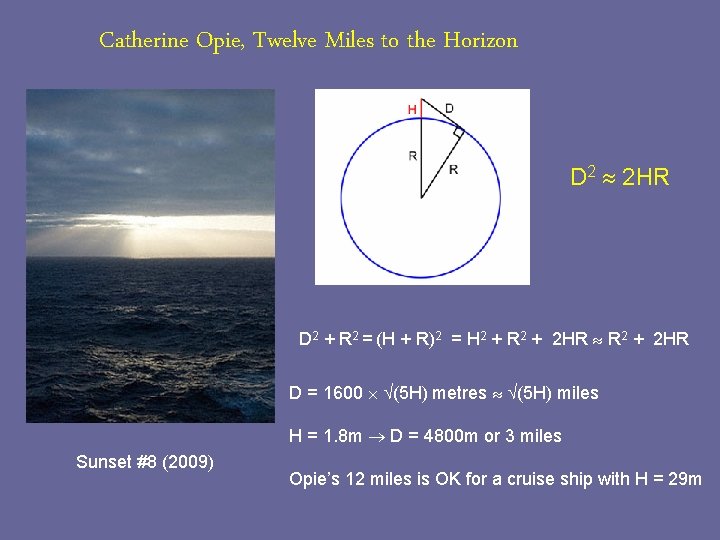
Catherine Opie, Twelve Miles to the Horizon D 2 2 HR D 2 + R 2 = (H + R)2 = H 2 + R 2 + 2 HR D = 1600 (5 H) metres (5 H) miles H = 1. 8 m D = 4800 m or 3 miles Sunset #8 (2009) Opie’s 12 miles is OK for a cruise ship with H = 29 m

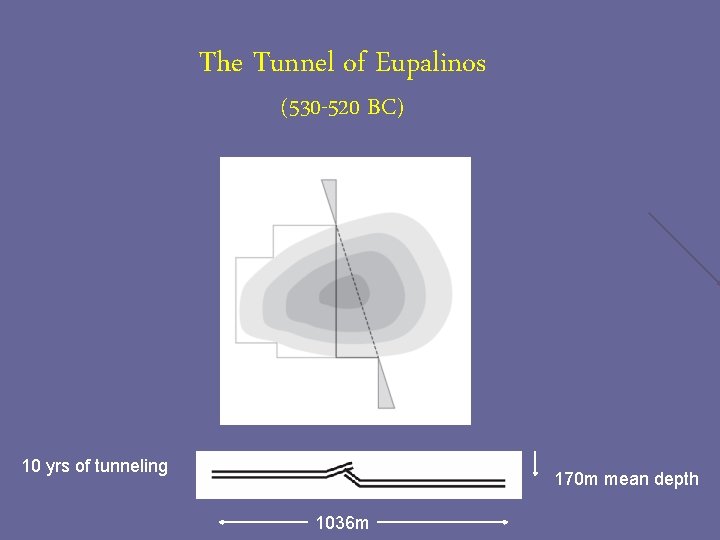
The Tunnel of Eupalinos (530 -520 BC) 10 yrs of tunneling 170 m mean depth 1036 m

The Rough and the Smooth

Self-similarity Helge von Koch’s ‘Snowflake’, 1904

Mandelbrot’s set (1980): the set of start points that stay at finite distances form the black region with its infinitely intricate boundary x x 2 – y 2 + a ; y 2 xy + b Any part of the boundary contains copies of the whole set

‘Jack the Dripper’ Jackson Pollock's ‘Convergence’ (1952), 237. 5 cm× 393. 7 cm, oil

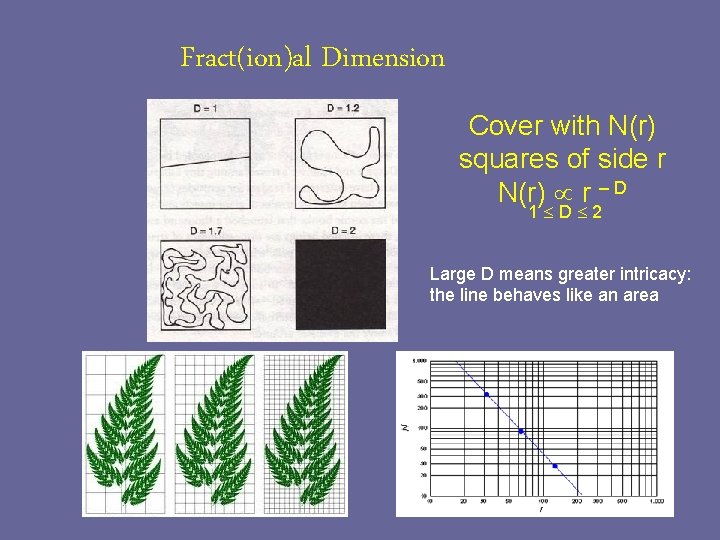
Fract(ion)al Dimension Cover with N(r) squares of side r N(r) r – D 1 D 2 Large D means greater intricacy: the line behaves like an area

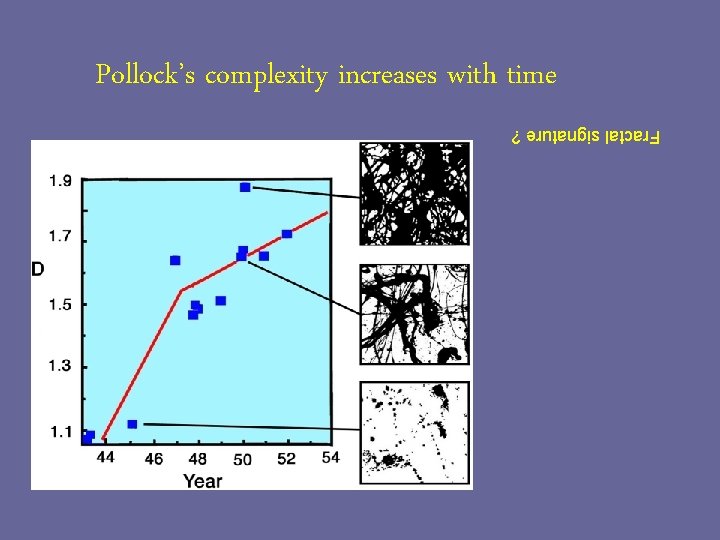
Pollock’s complexity increases with time Fractal signature ?

$Can you tell a Fake Pollock ? Can a fractal analysis distinguish true from$

Can you tell a Fake Pollock ? Can a fractal analysis distinguish true from fake? YES – Richard Taylor et al NO – Kate Jones-Smith et al Controversial!

String surface model: hyperbolic paraboloid by Fabre de Lagrange, 1872 Two bars equally spaced, each turns on an arm perpendicular to itself and one arm swings on a pillar; these arms can be ranged in one plane, and also turned end for end. Henry Moore, Bird Basket, 1939

Jerusalem Chords Suspension Bridge

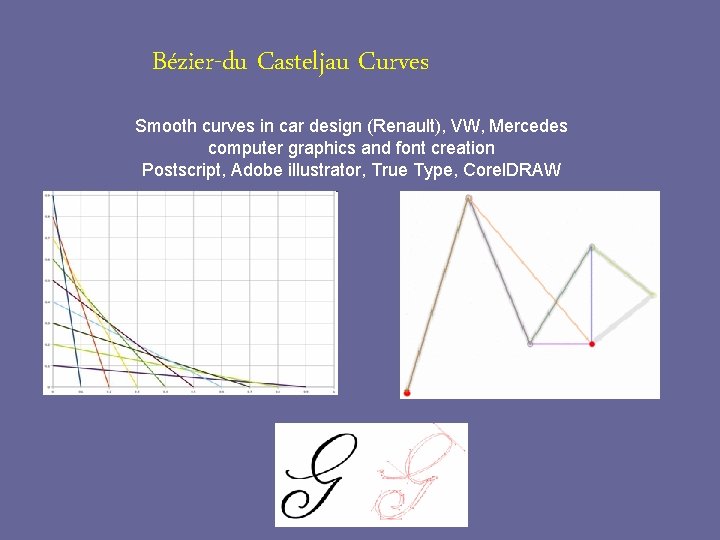
Bézier-du Casteljau Curves Smooth curves in car design (Renault), VW, Mercedes computer graphics and font creation Postscript, Adobe illustrator, True Type, Corel. DRAW

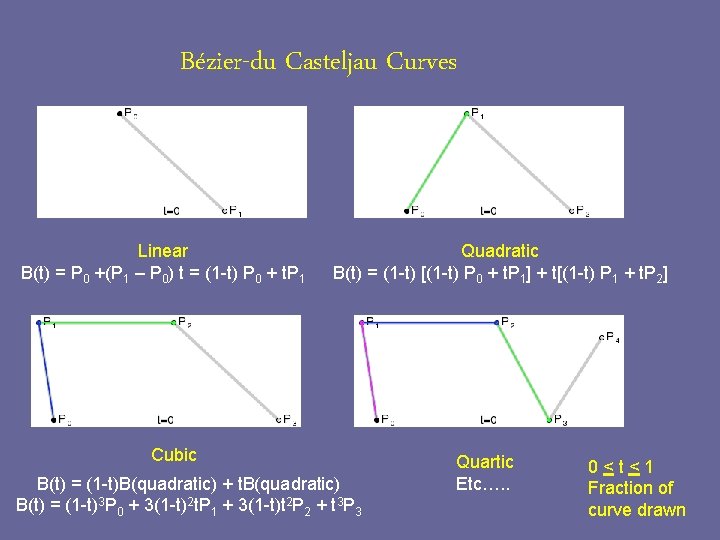
Bézier-du Casteljau Curves Linear B(t) = P 0 +(P 1 – P 0) t = (1 -t) P 0 + t. P 1 Quadratic B(t) = (1 -t) [(1 -t) P 0 + t. P 1] + t[(1 -t) P 1 + t. P 2] Cubic B(t) = (1 -t)B(quadratic) + t. B(quadratic) B(t) = (1 -t)3 P 0 + 3(1 -t)2 t. P 1 + 3(1 -t)t 2 P 2 + t 3 P 3 Quartic Etc…. . 0<t<1 Fraction of curve drawn

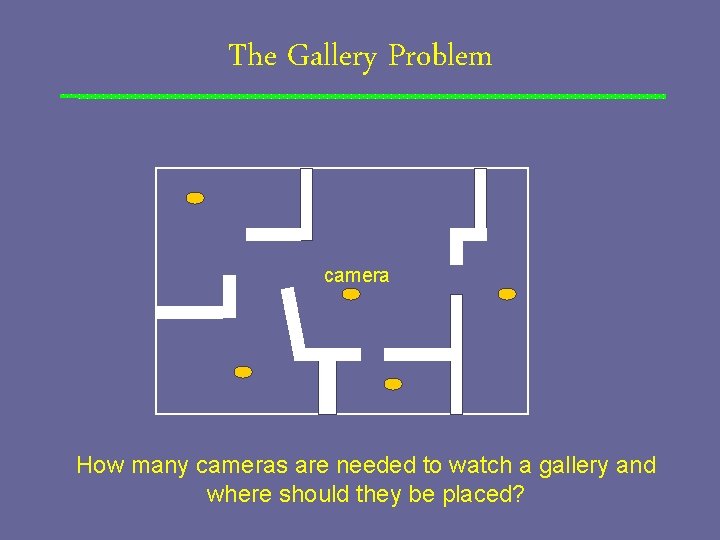
The Gallery Problem camera How many cameras are needed to watch a gallery and where should they be placed?

Simple Polygonal Galleries Regions with holes are not allowed and no self intersections convex polygon one camera is enough an arbitrary n-gon (n corners) ? cameras might be needed

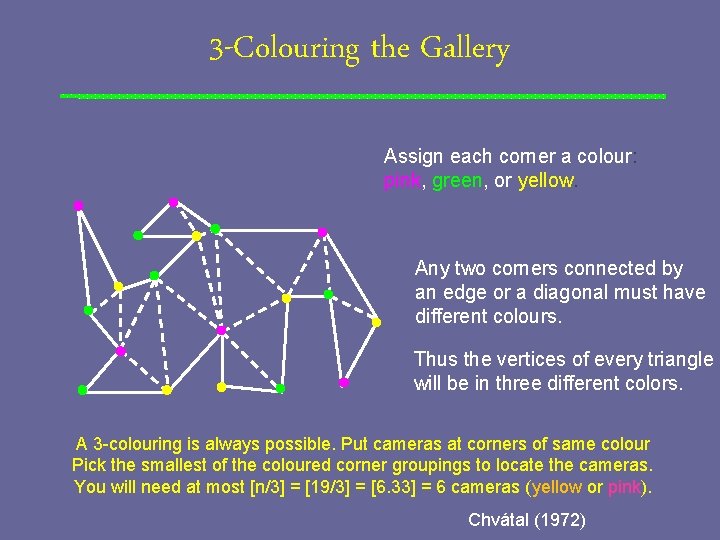
3 -Colouring the Gallery Assign each corner a colour: pink, green, or yellow. Any two corners connected by an edge or a diagonal must have different colours. Thus the vertices of every triangle will be in three different colors. A 3 -colouring is always possible. Put cameras at corners of same colour Pick the smallest of the coloured corner groupings to locate the cameras. You will need at most [n/3] = [19/3] = [6. 33] = 6 cameras (yellow or pink). Chvátal (1972)

Maths and Poetry Andrei Markov’s invention of mathematical textual analysis (1913) The statistical theory of non-independent sequences of events ‘Markov Processes’

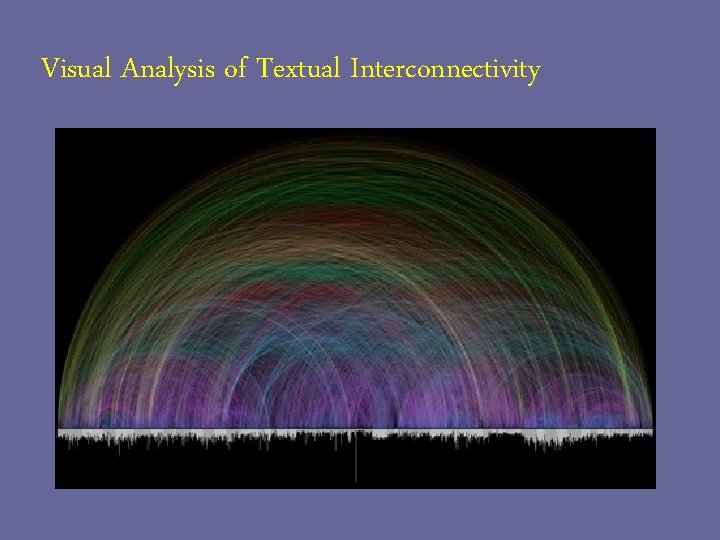
Visual Analysis of Textual Interconnectivity