Mathematics is a Language Examples University Iasi October

Mathematics is a Language Examples University Iasi October 2016 Dr. Ruprecht Witzel

Mathematics is a Language Content: 1. Introduction 2. Microeconomic Examples 3. Lotka-Volterra Equations 4. Other Economic Examples Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 2

Mathematics is a Language 1. Introduction • • Why should we study mathematics? Because: Mathematics is a Language! • • This sentence is the motto of the fundamental book Foundations of Economic Analysis of Paul A. Samuelson (1915 – 2009) – Copyright, 1947, Havard University Press – Samuelson was the first US-American economist to win the Nobel Memorial Prize in Economic Sciences in 1970 According to this book this sentence is from Josiah W. Gibbs, an US-American physicist (1839 – 1903) Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 3

Mathematics is a Language 1. Introduction • The characteristics of this language are: – The "sentences" of this language are mathematical formulas consisting of symbols – Pure mathematical formulas have no content-related meaning – But mathematical formulas can be interpreted – An interpretation of a set of suitable formulas may be a model to describe real phenomena – Sometimes, there are different interpretations of the same set of formulas possible Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 4

Mathematics is a Language 1. Introduction – The symbolic language to describe models with mathematical formulas is: • international • extremely precise, concise, exact • very compact, dense • very efficient – Example: If for a set of formulas exists a solution and different interpretations are possible then this solution is relevant for all corresponding interpretations, i. e. one has solutions for different models at the same time Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 5

Mathematics is a Language 1. Introduction • A formula may be right (correct) or wrong (incorrect) – Example: is a mathematical formula is a derived correct formula is a derived incorrect formula Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 6

Mathematics is a Language 1. Introduction • A pure formula without an interpretation of the symbols has no content-related meaning – Example: • This formula can be interpreted as a budget line as part of a microeconomic model to describe consumer behavior using the following interpretations: – constant amount of money to buy two goods – constant prices of good 1 and good 2 – consumed amounts of good 1 and good 2 Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 7

Mathematics is a Language 1. Introduction • A model and its implications may be true or false – Example: The true model to describe the covered track of the ideal free fall is given by the formula with for time and gravity (9. 81 m/s 2) – for the acceleration due to A false model would be described by the formula Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 8

Mathematics is a Language 1. Introduction • • A model and its implication are true as long there is no falsification Concerning the above two models of the ideal free fall one can show via experiments that the first model is the true model and the second one is not true In natural sciences the falsification of models and their implications is possible by well defined experiments and consequently "rather easy" In social sciences the falsification of models and their implications is much more difficult because it is not so easy to perform well defined experiments Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 9

Mathematics is a Language Content: 1. Introduction 2. Microeconomic Examples 3. Lotka-Volterra Equations 4. Other Economic Examples Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 10

Mathematics is a Language 2. Microeconomic Examples • • • Starting point are the following two formulas: (1) (2) What do they mean? – Nothing! With the assumptions the following statements and graphical illustration are possible Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 11

Mathematics is a Language 2. Microeconomic Examples • Formula (1) defines the following line • Formula (2) defines a cohort of strictly convex curves Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 12

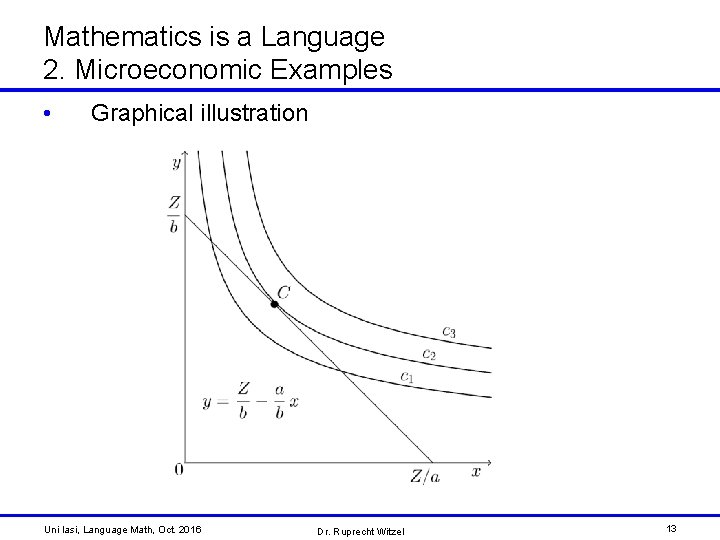
Mathematics is a Language 2. Microeconomic Examples • Graphical illustration Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 13

Mathematics is a Language 2. Microeconomic Examples • In the tangent point C the slope of the line defined by formula (1) is equal to the slope of the curve defined by formula (2) for • But there is still no content-related meaning Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 14

Mathematics is a Language 2. Microeconomic Examples • • • The two formulas (1) and (2) and the graph may obtain a content-related meaning by the following interpretation: We want to describe the behavior of a consumer who has a fixed amount of money to buy two goods so that he maximizes his utility; the prices of the two goods are given We make the following assignment: – constant amount of money to buy goods – consumed amount of good 1 – consumed amount of good 2 – constant price of good 1 – constant price of good 2 Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 15

Mathematics is a Language 2. Microeconomic Examples • Formula (1) can now be interpreted as the corresponding budget line (3) • In all points of the budget line the consumer spends all his given money to buy the two goods • The slope of the budget line is equal to the relationship of the given two prices of the two consumption goods with a negative sign Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 16

Mathematics is a Language 2. Microeconomic Examples • • • Formula (2) can now be interpreted as a cohort of indifference curves (4) In all points of an indifference curve the consumer has the same utility; i. e. he is indifferent with respect to all consumption bundles on this curve The indifference curves are strictly convex: Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 17

Mathematics is a Language 2. Microeconomic Examples • • The two formulas (3) and (4) together with the given interpretation of the symbols describe a microeconomic model to analyze consumer behavior In the following graph, the optimal consumption point is point C where the budget line is tangent to the indifference curve At the optimal consumption C the slope of the indifference curve is equal to the relationship of the prices (with a negative sign): At the optimal consumption point C the marginal rate of substitution, , is equal to the price relationship 18 Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel

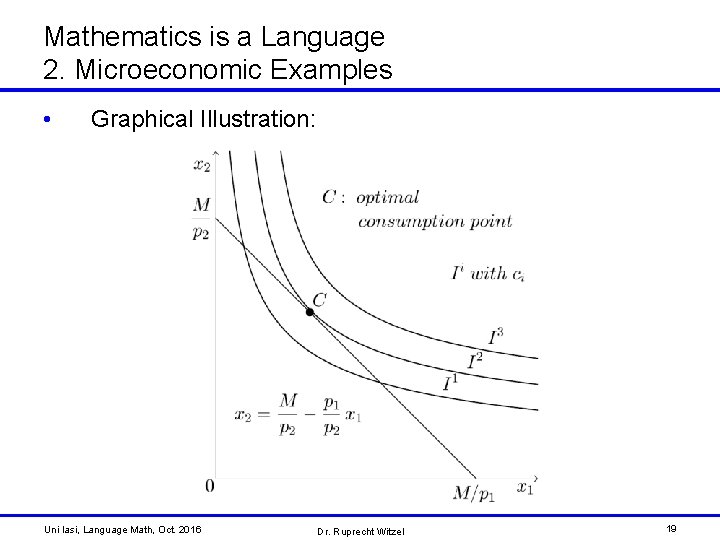
Mathematics is a Language 2. Microeconomic Examples • Graphical Illustration: Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 19

Mathematics is a Language 2. Microeconomic Examples • • The marginal rate of substitution, , can be interpreted as an internal transfer rate ("exchange rate") – It is a measure for the decrease (increase) of the amount of good 2, if the amount of good 1 is increased (reduced) by a marginal amount without changing the level of the preferences of the consumer The price relationship, , can be interpreted as an external transfer rate ("exchange rate") – It is a measure for the decrease (increase) of the bought amount of good 2, if the bought amount of good 1 is increased (reduced) by one unit Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 20

Mathematics is a Language 2. Microeconomic Examples • • Another interpretation of the formulas (1) and (2) is possible We can use these formulas to analyze the behavior of a firm We want to describe the behavior of a firm which wants to maximize the output for given production costs; there are two production factors with fixed prices We make the following assignment: – given production costs – input amount of production factor labor – input amount of production factor capital – given price of labor – given price of capital Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 21

Mathematics is a Language 2. Microeconomic Examples • Formula (1) can now be interpreted as the corresponding isocost line (5) • In all points of the isocost line the production costs of the firm are constant • The slope of the isocost line is equal to the relationship of the given two prices of the two production factors with a negative sign Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 22

Mathematics is a Language 2. Microeconomic Examples • Formula (2) can now be interpreted as a cohort of isoquant curves (6) • • In all points of an isoquant curve the output is constant The isoquant curves are strictly convex: Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 23

Mathematics is a Language 2. Microeconomic Examples • • The two formulas (5) and (6) together with the given interpretation of the symbols describe a microeconomic model to analyze firm behavior In the following graph, the optimal production point is point P where the isocost line is tangent to the isoquant curve At the optimal production point P the slope of the isoquant curve is equal to the relationship of the prices of the two production factors (with a negative sign): At the optimal production point P the marginal rate of substitution, , is equal to the price relationship Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 24

Mathematics is a Language 2. Microeconomic Examples • Graphical Illustration: Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 25

Mathematics is a Language 2. Microeconomic Examples • The marginal rate of substitution, , can be interpreted as an internal transfer rate ("exchange rate") – It is a measure for the decrease (increase) of the input factor capital, if the amount of the input factor labor is increased (reduced) by a marginal amount without changing the output level of the firm • The price relationship, , can be interpreted as an external transfer rate ("exchange rate") – It is a measure for the decrease (increase) of the input factor capital, if the input factor labor is increased (reduced) by one unit Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 26

Mathematics is a Language 2. Microeconomic Examples Consequence: • The same set of mathematical formulas can be interpreted in the context of a microeconomic model in at least two different ways to analyze – consumer behavior or – firm behavior Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 27

Mathematics is a Language 2. Microeconomic Examples • • • Even insurance demand can be analyzed in an analog manner For this purpose uncertainty is introduced as follows There are two states of nature – State occurs with the probability In state income is equal to and no loss occurs In state a loss of the amount occurs and the amount of income is then is a state contingent income bundle Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 28

Mathematics is a Language 2. Microeconomic Examples • Without insurance the situation can be illustrated as follows with an initial state contingent income bundle • The 45°-line is called security line because here in both states of nature holds Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 29

Mathematics is a Language 2. Microeconomic Examples Comparison: Consumer Behavior (CB) versus Insurance Demand (ID) • Optimization function – (CB): Utility function with two consumption goods • – Example: ; ; (ID): Expected utility function depending on the probabilities and , the corresponding amounts of income and an appropriate utility function for • Example: Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 30

Mathematics is a Language 2. Microeconomic Examples Comparison: Consumer Behavior (CB) versus Insurance Demand (ID) • Constraint – (CB): Budget line with constant prices two goods and given amount of money – of the (ID): "Budget line" with constant expected value of income which is equal to Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 31

Mathematics is a Language 2. Microeconomic Examples Comparison: Consumer Behavior (CB) versus Insurance Demand (ID) • "Iso-Curves" – (CB): Indifference curves with constant utility for the corresponding goods bundles Example: – (ID): Indifference curves with constant expected utility for the corresponding state contingent income bundles Example: Remark: To guarantee that these indifference curves are strictly convex additional assumptions are required Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 32

Mathematics is a Language 2. Microeconomic Examples Comparison: Consumer Behavior (CB) versus Insurance Demand (ID) • "Iso-Curves"; (ID) (cont. ) – The implicit function theorem (see 2. 3. Example 2) and the assumptions and imply – I. e. these indifference curves are strictly convex if for the utility function for decreasing positive marginal utility is assumed Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 33

Mathematics is a Language 2. Microeconomic Examples Comparison: Consumer Behavior (CB) versus Insurance Demand (ID) • "Iso-Curves"; (ID) (cont. ) – The assumption of non-saturation implies – The assumption is crucial, because • implies for – In these cases, there exists no optimal solution • In addition, the assumption with an ordinal ordering Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel is not compatible 34

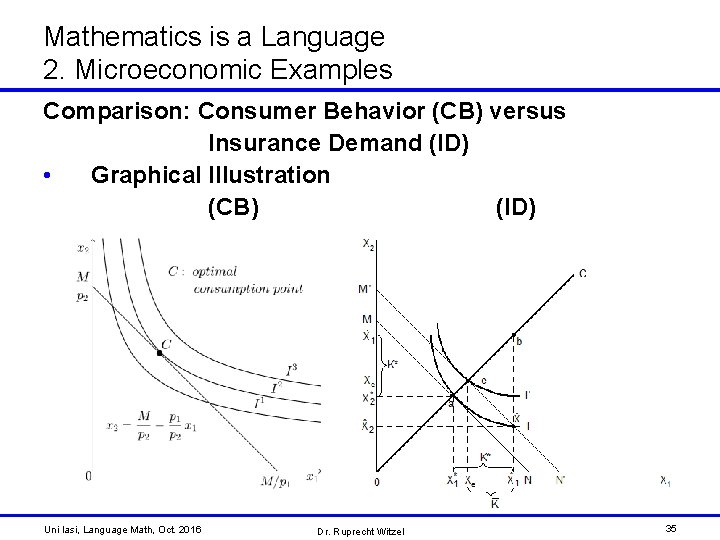
Mathematics is a Language 2. Microeconomic Examples Comparison: Consumer Behavior (CB) versus Insurance Demand (ID) • Graphical Illustration (CB) (ID) Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 35

Mathematics is a Language 2. Microeconomic Examples Comments concerning the insurance demand graph: • is the starting point • is the indifference curve belonging to the starting point • is the maximal premium for a full insurance – The corresponding point a is the point of intersection of the indifference curve and the security line • e is the optimal point for a full insurance – Here the corresponding indifference curve is tangent to the "budget line" through the starting point • is the fair premium for a full insurance – The corresponding point e is the point of intersection of the indifference curve , the security line and the "budget line" through the starting point Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 36

Mathematics is a Language Content: 1. Introduction 2. Microeconomic Examples 3. Lotka-Volterra Equations 4. Other Economic Examples Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 37

Mathematics is a Language 3. Lotka-Volterra Equations • The Lotka-Volterra equations are a pair of first-order, nonlinear differential equations to describe the dynamics of a prey-predator system: with eat number of prey (for example rabbits which eat grass) number of predator (for example foxes which rabbits) positive real parameters Remark: This chapter is based on Wikipedia Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 38

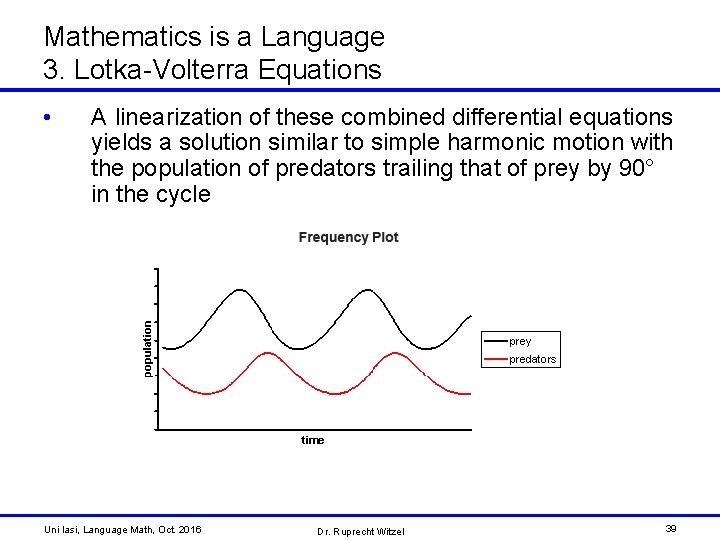
Mathematics is a Language 3. Lotka-Volterra Equations • A linearization of these combined differential equations yields a solution similar to simple harmonic motion with the population of predators trailing that of prey by 90° in the cycle Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 39

Mathematics is a Language 3. Lotka-Volterra Equations Possible different interpretations: • Biological Models: – The prey-predator interpretation for animals • was the first application of the Lotka-Volterra equations • is still used to analyze the development of the population of different pairs of animals • Medical Models: – The Lotka-Volterra equations are used in epidemic models to analyze spreading of infectious diseases Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 40

Mathematics is a Language 3. Lotka-Volterra Equations Possible different interpretations (cont. ): • Economic Models: – In economic models the Lotka-Volterra equations are usually used to analyze cyclical economic fluctuations; some examples: • The first one was Goodwin; in his model the prey is the employment rate and the predator is the wage ratio • In the model of Blümle, the prey is the variance of profits and the predator is the investment quota • In the model of Schohl, the prey is the variance of shifts in supply and the predator is the variance of the income return of the companies Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 41

Mathematics is a Language 3. Lotka-Volterra Equations Consequences: • The same set of mathematical formulas can be interpreted in different ways to analyze problems in totally different scientific areas: – Biology or – Medicine or – Economics • In addition, different interpretations are possible in each scientific area Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 42

Mathematics is a Language Content: 1. Introduction 2. Microeconomic Examples 3. Lotka-Volterra Equations 4. Other Economic Examples Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 43

Mathematics is a Language 4. Other Economic Examples In this chapter some other economic examples are presented where mathematics is an essential tool: • • • Econometrics Valuation of assets Equity rules Portfolio theory Linear Optimization Remark: This list is not exhaustive Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 44

Mathematics is a Language 4. Other Economic Examples • Econometrics: – Econometric models consist of mathematical formulas and numerically specified parameters to describe economic relationships – Mathematics is used as a formal language and statistical methods are used to determine the numerical values of the parameters – Target is often a model of the national economy as a whole or of parts of it Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 45

Mathematics is a Language 4. Other Economic Examples • Econometrics (cont. ): – Econometric models are used amongst other things to • analyze economic phenomena as e. g. – determination of demand functions • test theoretical economic models as e. g. – Keynesian or Monetarist oriented concepts • predict relevant economic figures as e. g. – Gross Domestic Product (GDP) – inflation rate – unemployment rate Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 46

Mathematics is a Language 4. Other Economic Examples • Valuation of assets: – The valuation of "normal" bonds, shares or real estate is normally no issue – In contrast, the valuation of derivatives requires sophisticated mathematical knowledge • E. g. the Black-Scholes-Model to determine the price of options is based on a stochastic differential equation – These ideas are strongly influenced by established physical concepts Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 47

Mathematics is a Language 4. Other Economic Examples • Equity rules: – Equity of a company is defined as assets minus liabilities – Especially for banks and insurance companies the new regulatory rules to determine the minimal amount of equity are rather complicate • They often use stochastic simulations Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 48

Mathematics is a Language 4. Other Economic Examples • Portfolio theory: – The modern portfolio theory since Markowitz is based on mathematical models – The return of the portfolio is appreciated but the volatility of the portfolio is judged as a risk – The issue to determine an efficient portfolio is often to achieve: • more return for the same risk or • less risk for the same return Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 49

Mathematics is a Language 4. Other Economic Examples • Linear Optimization: – Objective of linear optimization is the maximization or minimization of a linear target function subject to constraints – A typical example is the transport problem where one or several products should be carried from several supply stations to several demand destinations – An usual method to solve this issue is the Simplex Algorithm using the Gauss Elimination Method • These topics are part of your lecture Mathematics applied in Economics Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 50

Mathematics is a Language 4. Other Economic Examples • Linear Optimization (cont. ): – One of the first applications of the Simplex Algorithm was the so called diet problem • In this application published in 1947, the diet problem consists in minimizing the costs for feeding US-American soldiers with given aliments (as e. g. potatoes, meat, vegetables etc. ) subject to the constraint that the food contains minimal amounts of ingredients (as e. g. protein, fat, carbohydrates, vitamin etc. ) Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 51

Mathematics is a Language Last but not least, I hope I was – at least a little bit – successful in showing you that it is worthwhile to study the language Mathematics Uni Iasi, Language Math, Oct. 2016 Dr. Ruprecht Witzel 52