Mathematics for Computing Lecture 2 Computer Logic and


















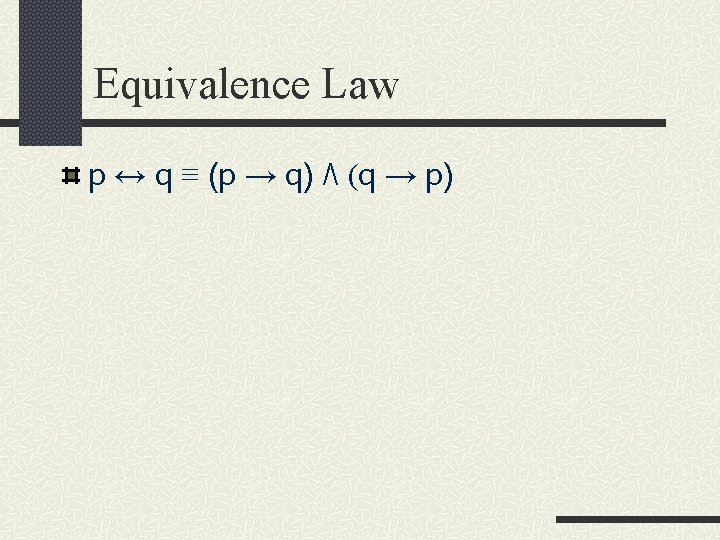










- Slides: 33

Mathematics for Computing Lecture 2: Computer Logic and Truth Tables Dr Andrew Purkiss-Trew Cancer Research UK a. purkiss@mail. cryst. bbk. ac. uk

Logic Propositions Connective Symbols / Logic gates Truth Tables Logic Laws

Propositions Definition: A proposition is a statement that is either true or false. Which ever of these (true or false) is the case is called the truth value of the proposition.

Connectives Compound proposition e. g. ‘If Brian and Angela are not both happy, then either Brian is not happy or Angela is not happy’ Atomic proposition: ‘Brian is happy’ ‘Angela is happy’ Connectives: and, or, not, if-then

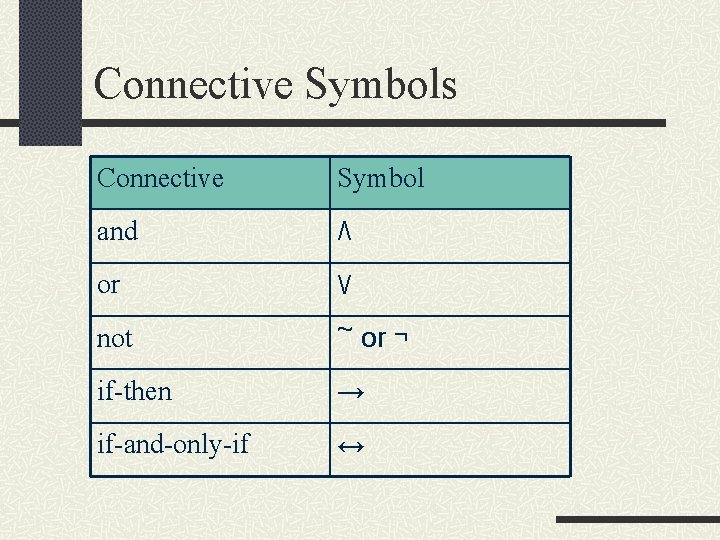
Connective Symbols Connective Symbol and ٨ or ٧ not ~ or ¬ if-then → if-and-only-if ↔

Conjugation Logical ‘and’ Symbol ٨ Written p ٨ q Alternative forms p & q, pq Logic gate version p q pq

Disjunction Logical ‘or’ Symbol ٧ Written p ٧ q Alternative form p + q Logic gate version p q p+q

Negation Logical ‘not’ Symbol ~ Written ~p Alternative forms ¬p, p’, p Logic gate version p ~p

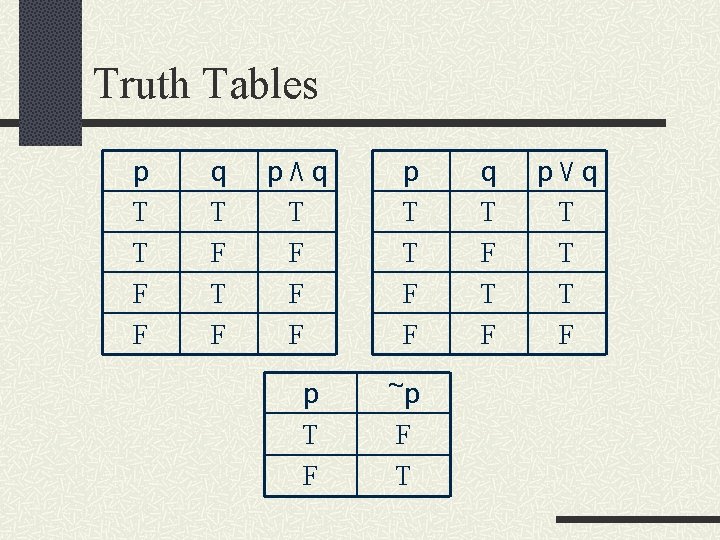
Truth Tables p T T F F q T F p٨ q T F F F p T T F F p T F ~p F T q T F p٧ q T T T F

Compound Propositions ~(p ٨ ~q) p q ~q p ٨~q ~(p ٨ ~q) T T F F T F F T

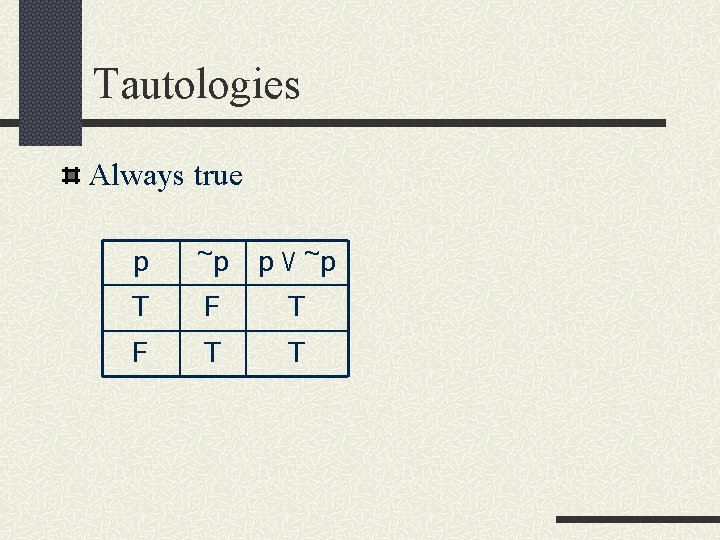
Tautologies Always true p ~p p ٧ ~p T F T T

Contradictions Always false p ~p p ٨ ~p T F F F T F

Website for Lecture Notes http: //www. cryst. bbk. ac. uk/~bpurk 01/Mf. C/index 2007. html
End of First Logic 1? Place marker

Mathematics for Computing Lecture 3: Computer Logic and Truth Tables 2 Dr Andrew Purkiss-Trew Cancer Research UK a. purkiss@mail. cryst. bbk. ac. uk

Logical Equivalence Logical ‘equals’ Symbol ≡ Written p ≡ p p T T F F q T F ~p F F T T ~q F T ~p ٨ ~q ~(~p ٨ ~q) p ٧ q F T T T F F

Conditional Logical ‘if-then’ Symbol → Written p → q p T T F F q T F p→q T F T T

Biconditional Logical ‘if and only if’ Symbol ↔ Written p ↔ q p T T F F q T F p↔q T F F T

converse and contrapositive The converse of p → q is q → p The contrapositive of p → q is ~q → ~p

Laws of Logic Laws of logic allow use to combine connectives and simplify propositions.

Double Negative Law ~~p≡p

Implication Law p → q ≡ ~p ٧ q
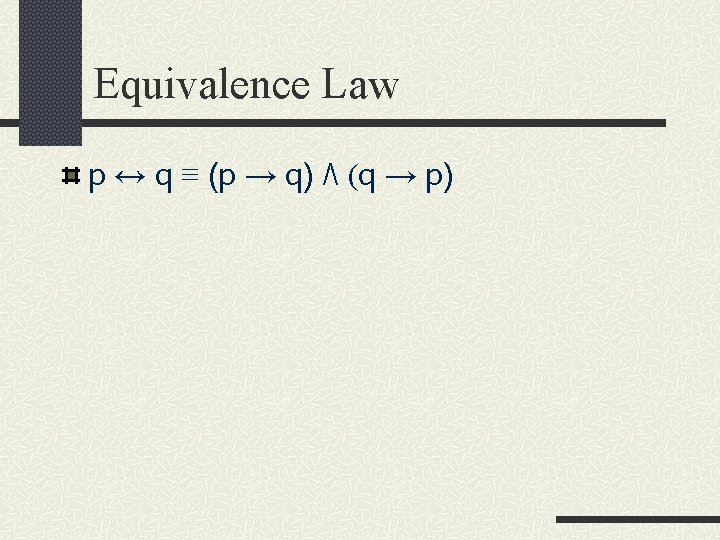
Equivalence Law p ↔ q ≡ (p → q) ٨ (q → p)

Idempotent Laws p٨ p≡p p٧ p≡p

Commutative Laws p٨ q≡q٨ p p٧ q≡q٧ p

Associative Laws p ٨ (q ٨ r) ≡ (p ٨ q) ٨ r p ٧ (q ٧ r) ≡ (p ٧ q) ٧ r

Distributive Laws p ٨ (q ٧ r) ≡ (p ٨ q) ٧ (p ٨ r) p ٧ (q ٨ r) ≡ (p ٧ q) ٨ (p ٧ r)

Identity Laws p٨ T≡p p٧ F≡p

Annihilation Laws p٨ F≡F p٧ T≡T

Inverse Laws p ٨ ~p ≡ F p ٧ ~p ≡ T

Absorption Laws p ٨ (p ٧ q) ≡ p p ٧ (p ٨ q) ≡ p

de Morgan’s Laws ~(p ٨ q) ≡ ~p ٧ ~q ~(p ٧ q) ≡ ~p ٨ ~q
