Mathematics for Computer Science MIT 6 042 J18

Mathematics for Computer Science MIT 6. 042 J/18. 062 J Combinatorics I Copyright © Radhika Nagpal, 2002. Prof. Albert Meyer & Dr. Radhika Nagpal March 17, 2002 1

Counting in Algorithms • How many different ways can 3 colors be assigned to an n-node graph? • How many different mappings need to be checked to see if two arbitrary n-node graphs are isomorphic? • How many stable pairings are there between n girls and n boys? March 17, 2002 2

Counting in Algorithms What is the minimum number of binary comparisons needed to sort n numbers? What is the best any algorithm could possibly do? March 17, 2002 3

Counting in Games • How many different initial positions exist for a rubix cube? • How many different chess boards can exist after 3 moves? After 6 moves? • How many weighings do you need to find one counterfeit coin amongst 12 coins? March 17, 2002 4

Counting in Probability of an event: # event outcomes total # outcomes March 17, 2002 5

Counting in Probability What is the probability of getting two jacks in a poker hand? March 17, 2002 6

Counting Techniques • • • Bijections Sum Rule, Inclusion-Exclusion Product Rule Pigeonhole Principle Trees Permutations March 17, 2002 7

Counting Techniques • • • Bijections Sum Rule, Inclusion-Exclusion Product Rule Pigeonhole Principle Trees Permutations March 17, 2002 8

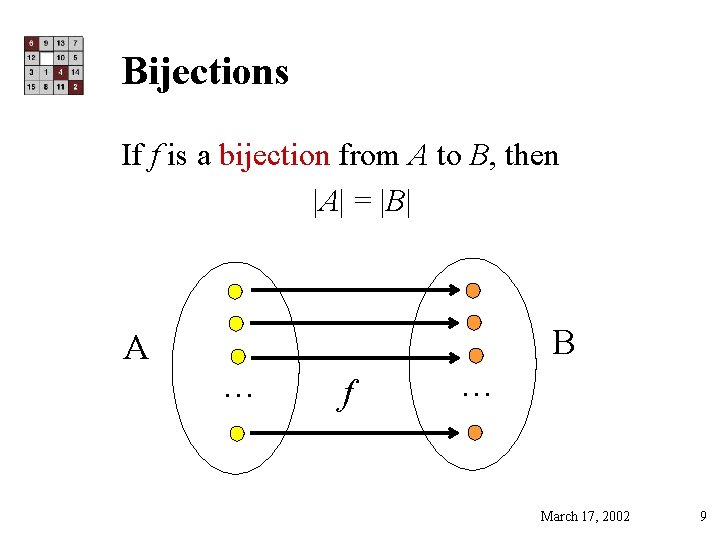
Bijections If f is a bijection from A to B, then |A| = |B| A B … f … March 17, 2002 9

Sum Rule If sets A and B are disjoint, then |A B| = |A| + |B| A B What if A and B are not disjoint? March 17, 2002 10

Inclusion-Exclusion (2 Sets) For two arbitrary sets A and B A B March 17, 2002 11

Inclusion-Exclusion (2 Sets) Corollary. Boole’s Law: |A B| |A| + |B| A B March 17, 2002 12

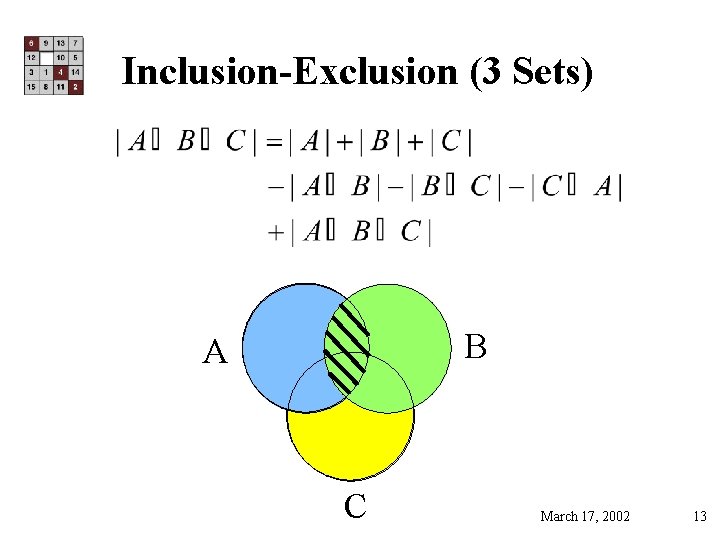
Inclusion-Exclusion (3 Sets) B A C March 17, 2002 13

Product Rule If |A| = m and |B| = n, then |A x B| = mn March 17, 2002 14

Product Rule If |A| = m and |B| = n, then |A B| = mn A = {a, b, c, d}, B = {1, 2, 3} A B = {(a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3), (c, 1), (c, 2), (c, 3), (d, 1), (d, 2), (d, 3)} March 17, 2002 15

Product Rule: Counting Strings The number of 4 -bit strings from the alphabet A = {0, 1} = |A A A A| = 2· 2· 2· 2 = March 17, 2002 16

Product Rule: Tree 1 1 0 1111 1110 1101 1100 1011 … 0 0000 March 17, 2002 17

Product Rule: Counting Strings The number of n-bit strings from an alphabet, A, of size m is n m March 17, 2002 18

Example Given a set, A, how many subsets are there? . . . |P(A)| ? A = {a, b, c} P(A) = { , {a}, {b}, {c}, {a, b}, {b, c}, {c, a}, {a, b, c}} March 17, 2002 19

Bijection: P(A) and Binary Strings A= {a 1, a 2, a 3, a 4, a 5, ……, an} String = 1 0 1 1 1 0 … 0 Subset = {a 1, a 3, a 4, a 5} Exact correspondence: = |n-bit binary strings| = |P(A)| March 17, 2002 20

Pigeonhole Principle If you have more pigeons than pigeonholes, March 17, 2002 21

Pigeonhole Principle then some hole must have two pigeons! March 17, 2002 22

Example: Birthdays 366 people: at least two must have the same birthday (day/month). 731 people: three must have same birthday…. March 17, 2002 23

In-class Problems March 17, 2002 24

Summary • Sum rule If sets A and B are disjoint, then |A B| = |A| + |B| • Inclusion Exclusion • Product Rule If |A| = m and |B| = n, then |A B| = mn • Pigeonhole Principle If more pigeons than holes, then 2 in some hole. March 17, 2002 25

March 17, 2002 26

Counting Strings with 7 s • False Argument – Counted numbers with multiple 7 s many times March 17, 2002 27

A Correct Argument • All 4 -digit numbers with at least one 7 = all possible 4 -digit numbers, minus 4 -digit numbers with no 7 s. • Both of these are easy to count March 17, 2002 28

An Alternate Counting? • Is this argument correct? March 17, 2002 29

Algebra or Calculator • Are these two the same? March 17, 2002 30

How do you know if it is correct? • Many ways of counting the same thing • How do you know you got it right? – Algebra, calculator – Prove it! March 17, 2002 31

Proving Correctness Prove that you counting correctly: – Prove that you counted everything – Prove that you counted nothing twice March 17, 2002 32

Another Pigeonhole Problem • Say that we have 6 people, such that every pair of people are either friends or strangers, then – there is always a set of 3 friends or 3 strangers March 17, 2002 33

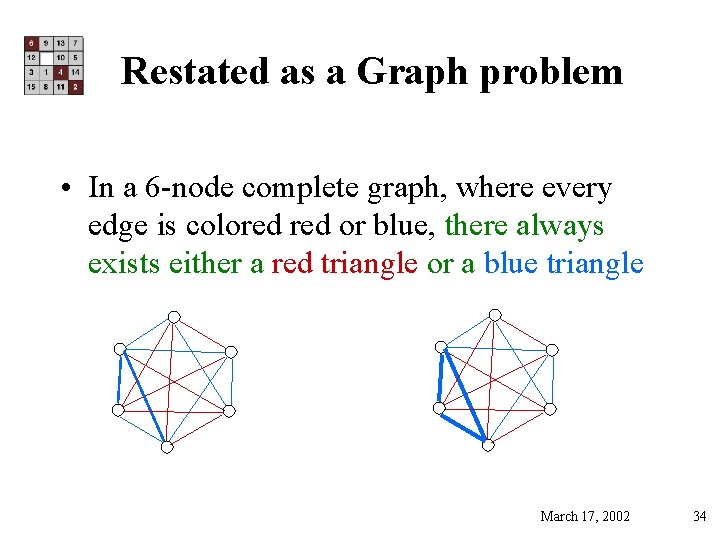
Restated as a Graph problem • In a 6 -node complete graph, where every edge is colored or blue, there always exists either a red triangle or a blue triangle March 17, 2002 34

Not always so easy…. How many people do you need before you are guaranteed to have a set of six that know each other? Paul Erdos’s answer: If aliens required you answer this in a year, throw in the towel and strike preemptively…. Ramsey numbers: R(3, 3) = 6, R(6, 6) = ? ? March 17, 2002 35

Next lecture • • Trees, Permutations, r-Permutations Importance of mapping Functions and strings – How many possible functions, – How many possible bijections? March 17, 2002 36

Important technique: Matching • Make a mapping between a given problem and a set of known cardinality (or at least one we know how to count…): • Functions binary strings • Lists trees • Graphs, Relations matrices • Strings, polynomials balls and bins March 17, 2002 37