Mathematics for Computer Graphics Lecture Summary n Matrices

Mathematics for Computer Graphics

Lecture Summary n Matrices ¨ Some fundamental operations n Vectors ¨ Some fundamental operations n Geometric Primitives: ¨ Points, Lines, Curves, Polygons

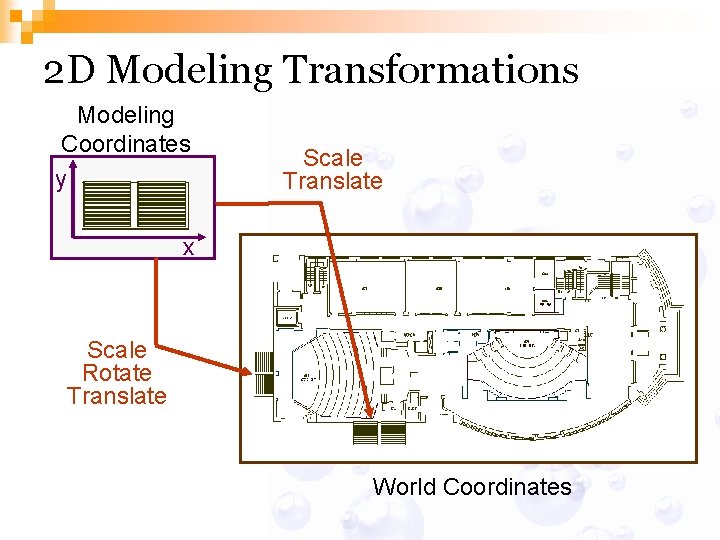
2 D Modeling Transformations Modeling Coordinates y Scale Translate x Scale Rotate Translate World Coordinates

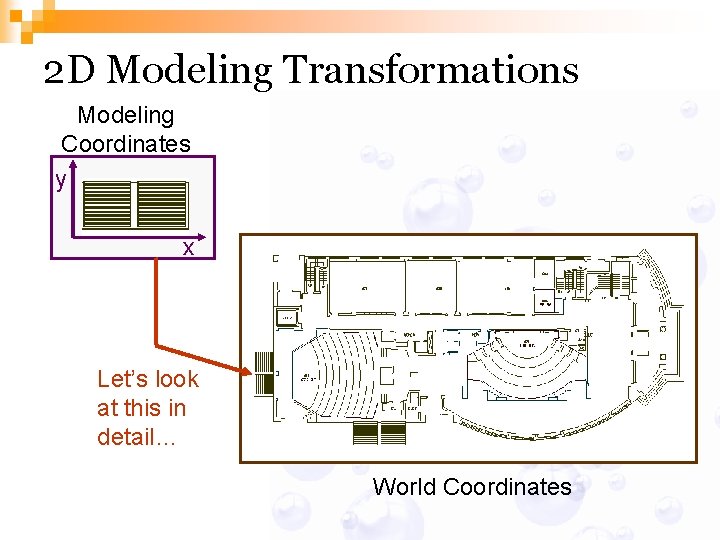
2 D Modeling Transformations Modeling Coordinates y x Let’s look at this in detail… World Coordinates

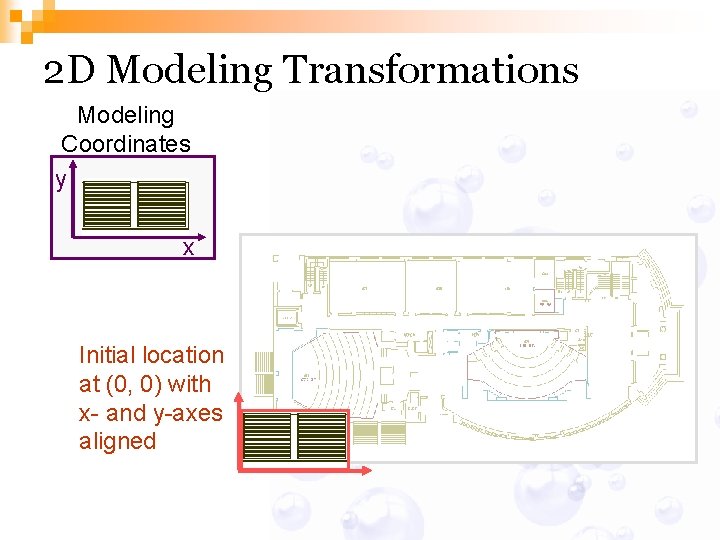
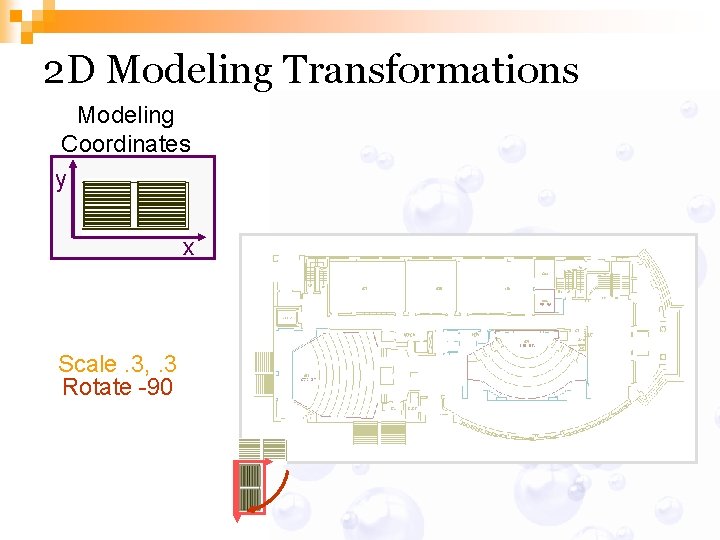
2 D Modeling Transformations Modeling Coordinates y x Initial location at (0, 0) with x- and y-axes aligned

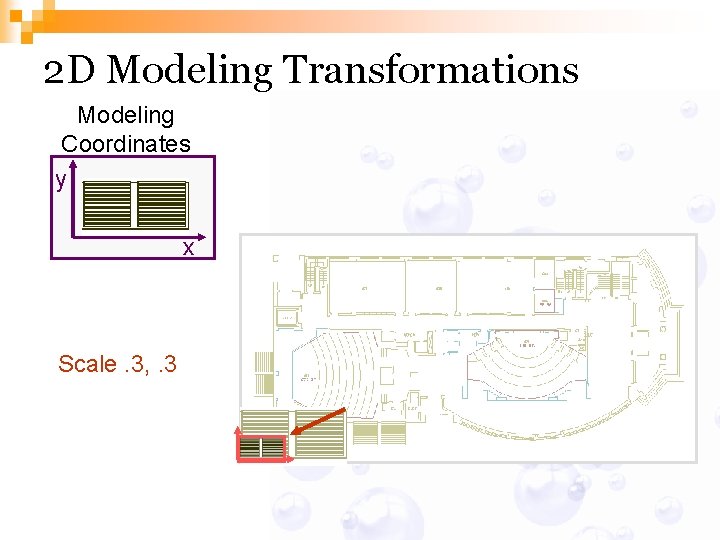
2 D Modeling Transformations Modeling Coordinates y x Scale. 3, . 3 Rotate -90 Translate 5, 3

2 D Modeling Transformations Modeling Coordinates y x Scale. 3, . 3 Rotate -90 Translate 5, 3

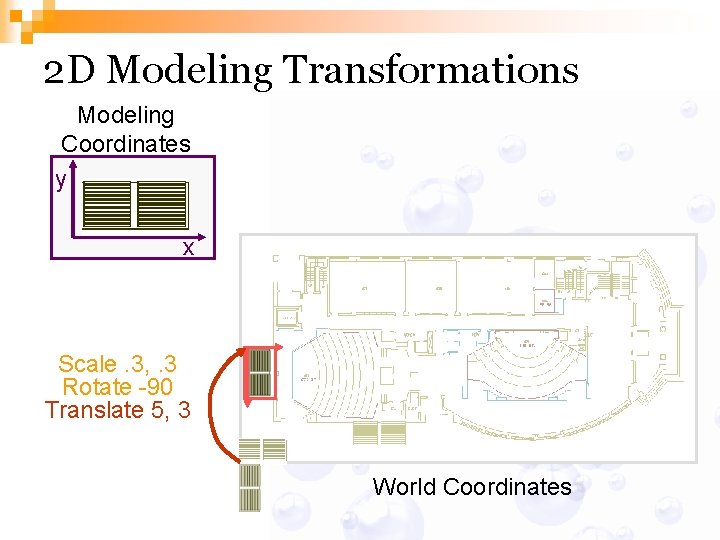
2 D Modeling Transformations Modeling Coordinates y x Scale. 3, . 3 Rotate -90 Translate 5, 3 World Coordinates

Matrices n n n A matrix is a rectangular array of elements (numbers, expression, or function) A matrix with m rows and n columns is said to be an m-by-n matirx ( matrix), e. g In general, we can write an m-by-n matrix as

Matrices n A matrix with a single row or a single column represent a vector Single row : 1 -by-n matrix is a row vector n Single column : n-by-1 matrix is a column vector n A square matrix is a matrix has the same number of rows as columns n In graphics, we frequently work with two-by-two, three-by-three, and fourby-four matrices n The zero matrix The identity matrix A diagonal matrix n n n

Scalar Multiplication n To multiply a martix A by a scalar value s, we multiply each element amn by the scalar n Ex. , find 3 A = ?

Matrix Addition n Two matrices A and B may be added together when these two matrices have the same number of rows and column the same shape The sum is obtained by adding corresponding elements. n Ex. n , find A+B = ?

Matrix Multiplication 1 x 3 2 x 2 3 x 1 2 x 2 3 x 3 1 x 1 2 x 2 3 x 1

Matrix Multiplication 1 x 3 2 x 2 3 x 1 2 x 2 3 x 3 1 x 1 2 x 2 3 x 1

Matrix Multiplication 1 x 3 2 x 2 3 x 1 2 x 2 3 x 3 1 x 1 2 x 2 3 x 1

Matrix Multiplication 1 x 3 2 x 2 3 x 1 2 x 2 3 x 3 1 x 1 2 x 2 3 x 1

Matrix Multiplication 1 x 3 2 x 2 3 x 1 2 x 2 3 x 3 1 x 1 2 x 2 3 x 1

Matrix Multiplication 1 x 3 2 x 2 3 x 1 2 x 2 3 x 3 1 x 1 2 x 2 3 x 1

Matrix Multiplication 1 x 3 2 x 2 3 x 1 2 x 2 3 x 3 1 x 1 2 x 2 3 x 1

Matrix Multiplication 1 x 3 2 x 2 3 x 1 2 x 2 3 x 3 1 x 1 2 x 2 3 x 1

Matrix Multiplication 1 x 3 2 x 2 3 x 1 2 x 2 3 x 3 1 x 1 2 x 2 3 x 1

Matrix Multiplication 1 x 3 2 x 2 3 x 1 2 x 2 3 x 3 1 x 1 2 x 2 3 x 1

Matrix Multiplication 1 x 3 2 x 2 3 x 1 2 x 2 3 x 3 1 x 1 2 x 2 3 x 1

Matrix Multiplication e. g. :

Matrix Multiplication e. g. :

Matrix Multiplication e. g. :

Matrix Multiplication e. g. :

Matrix Multiplication e. g. :

Matrix Multiplication e. g. :

Matrix Multiplication e. g. :

Matrix Multiplication e. g. :

Matrix Multiplication e. g. :

Matrix Multiplication e. g. :

Matrix Multiplication e. g. :

Matrix Multiplication e. g. :

Warning!!! but (AB)C = A(BC) n n A(B+C) = AB + AC n (A+B)C = AC + BC n (AB)T = BTAT n A(s. B) = s. AB

Determinant of a Matrix n

Matrix Inverse n