Mathematics Behind the Rubiks Cube Mathematical Modeling Bihan

Mathematics Behind the Rubik’s Cube Mathematical Modeling Bihan Zhang and Trachelle Mc. Donald C. E. Jordan High School and Pamlico High School 2008

Problem n Explore the mathematics behind Rubik’s cube using simulations in VPython ¨ Explain how permutation relate to the Rubik’s cube ¨ Explain how group theory relate to the Rubik’s cube http: //upload. wikimedia. org/ wikipedia/commons/6/67/R ubiks_revenge_scrambled. j pg

Outline History n Permutations n Operations with Groups n Triangle Operations n Rubik’s Cube Operations n Conclusion n http: //www. smh. com. au/ffximage/200 7/10/04/cube_narrowweb__300 x 392, 0. jpg

Inventor: Ernö Rubik -Born in Budapest, Hungary -Architect -Founder of Rubik Studio http: //pics. livejournal. com/sullenfish/pic/ 0000801 h/s 640 x 480

History n Invented by Ernő Rubik in 1974 n “No arrangement of the http: //www. smh. com. au/ffximage/200 7/10/04/cube_narrowweb__300 x 392, 0. jpg 3 x 3 x 3 Rubik's Cube requires more than 20 moves to solve. ” n “The Current World Record is 7. 08 Seconds. " http: //upload. wikimedia. org/wikipedia/en/thu mb/1/1 e/Pocket_cube. jpg/200 px. Pocket_cube. jpg

Permutations n “A permutation is an arrangement of objects in different orders. ” ¨ 1 2 3 ¨ 1 3 2 ¨ 2 1 3 ¨ 2 3 1 ¨ 3 1 2 ¨ 3 2 1

Permutations Original Permuted t = u = 1 1 2 2 3 3 1 2 2 3 3 1 t (1) = 2 t (2) = 3 1 3 2 1 u (1) = 3 u (2) = 1 t (3) = 1 3 2 u (3) = 2

Permutations for a Rubik’s Cube 43, 252, 003, 274, 489, 856, 000 http: //upload. wikimedia. org/wikipedia/co mmons/thumb/a/a 6/Rubik's_cube. svg/4 80 px-Rubik's_cube. svg. png 3, 674, 160 http: //upload. wikimedia. org/wikipedia/commons/thumb/4/43/Solved_2 x 2 x 2. jpg/6 00 px-Solved_2 x 2 x 2. jpg

What is a Group? A set of elements plus a binary operation n A group has the following properties: n ¨ Closure ¨ Identity element ¨ Inverse ¨ Associativity n Commutative 1+2 = 3 1+0 = 1 1+(-1) = 0 1+(2+3) = (1+2)+3 1+2 = 2+1

Operations with Groups 1. 1= v= t= w= u= x= 2. 3. 4. 5. 6. 7. tx=? t(x(1))= ? x(1)=1 t(1)=2 t(x(2))= ? x(2)=3 t(3)=1 t(x(3))=? 9. x(3)=2 10. t(2)=3 8. tx=(213)=v

Operations with Groups 1= v= 1. w= 3. 4. u= x= x(t(3))=? 9. t(3)=1 10. x(1)=1 8. 2. t= xt=? 5. 6. 7. x(t(1))= ? t(1)=2 x(2)=3 x(t(2))= ? t(2)=3 x(3)=2 xt=(321)=w
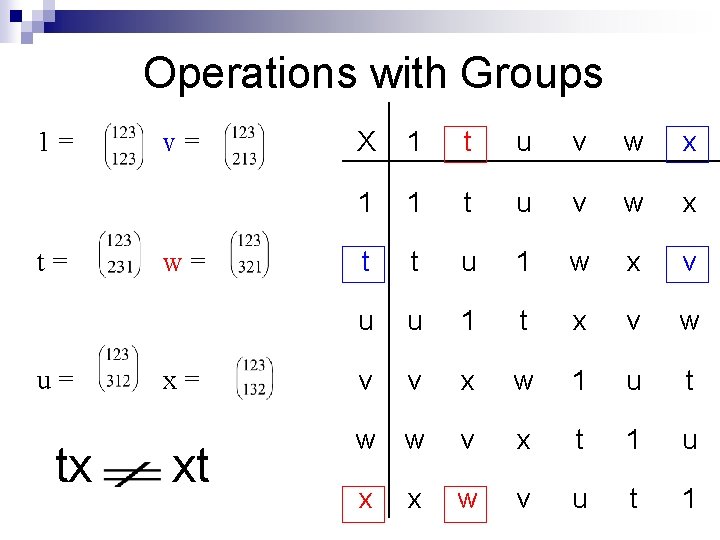
Operations with Groups 1= t= u= v= w= x= tx xt X 1 t u v w x 1 1 t u v w x t t u 1 w x v u u 1 t x v w v v x w 1 u t w w v x t 1 u x x w v u t 1

Operations with Groups 1= t= u= v= w= x= X 1 t u v w x 1 1 t u v w x t t u 1 w x v u u 1 t x v w v v x w 1 u t w w v x t 1 u x x w v u t 1
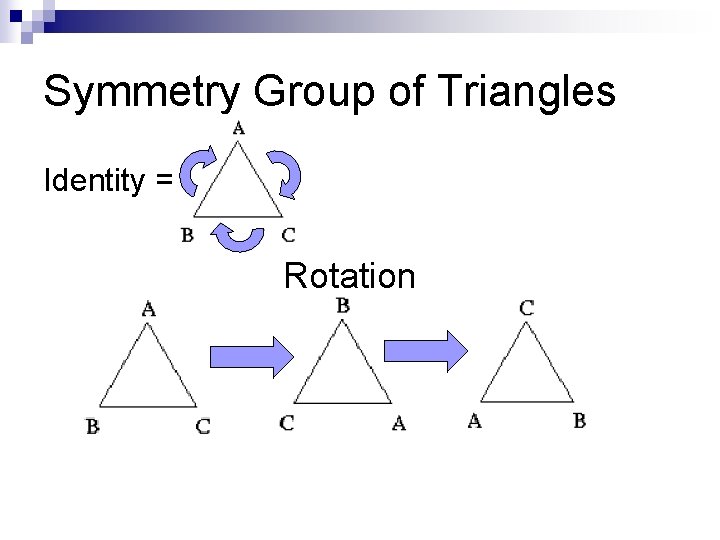
Symmetry Group of Triangles Identity = Rotation

Symmetry Group of Triangles Identity = Reflection
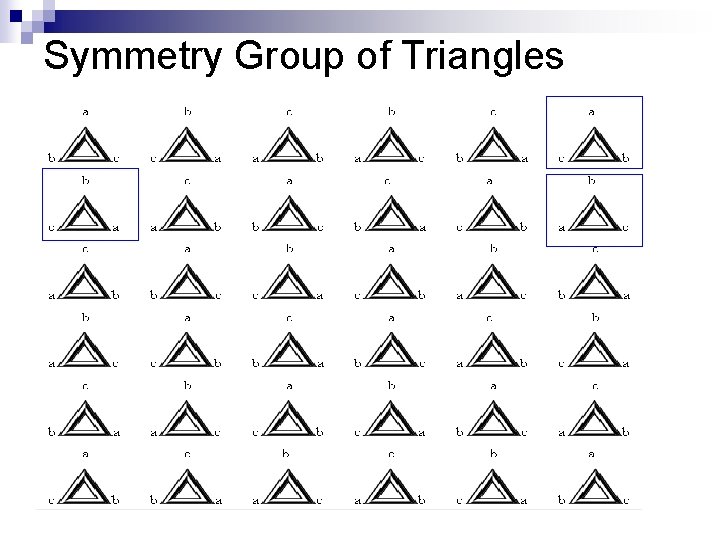
Symmetry Group of Triangles
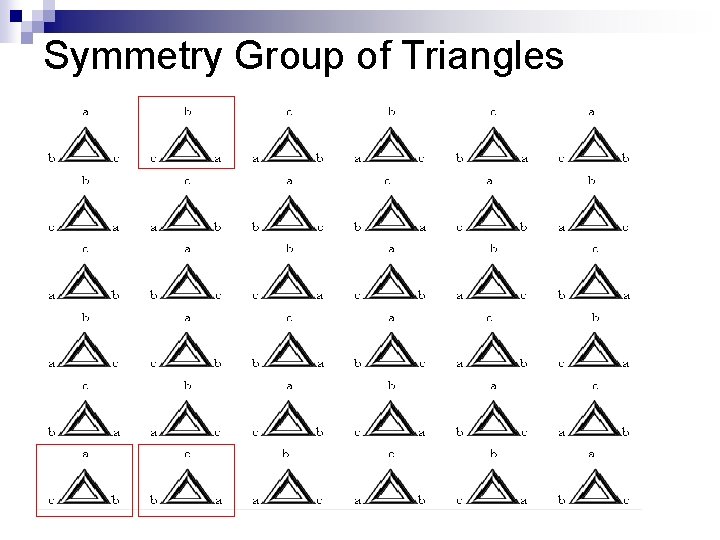
Symmetry Group of Triangles
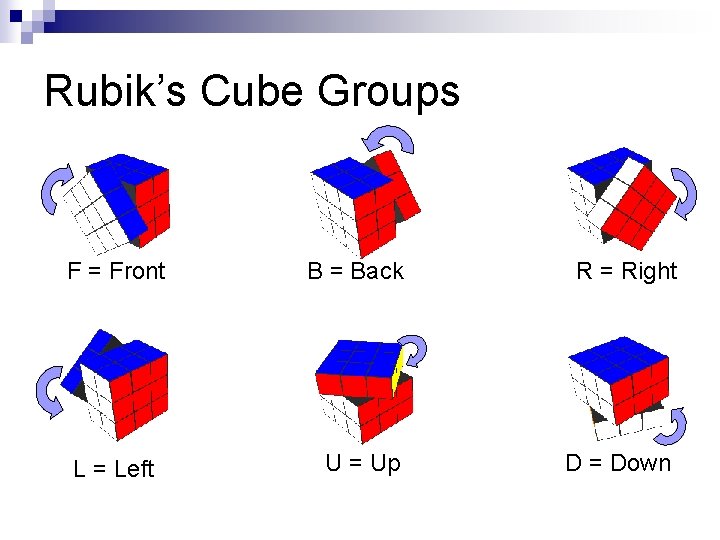
Rubik’s Cube Groups F = Front L = Left B = Back R = Right U = Up D = Down
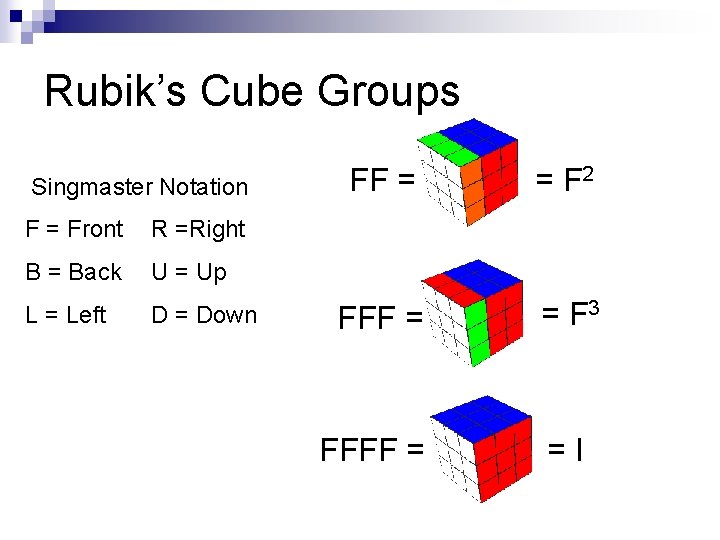
Rubik’s Cube Groups Singmaster Notation FF = = F 2 FFF = = F 3 FFFF = = I F = Front R =Right B = Back U = Up L = Left D = Down

Our Simulation
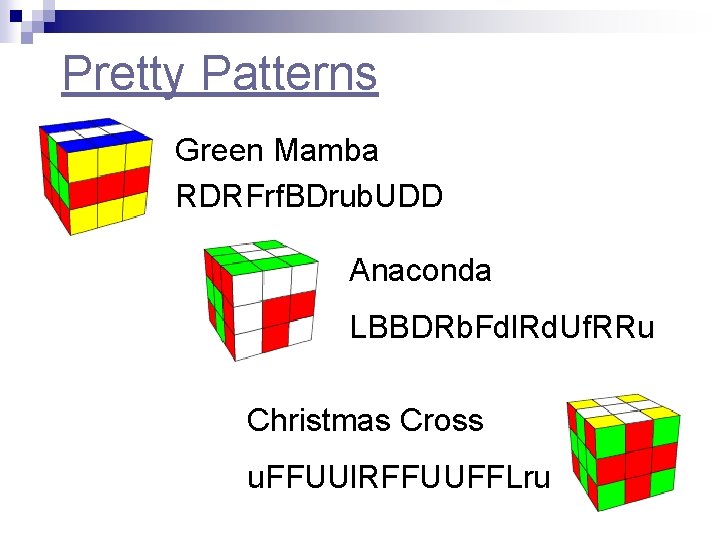
Pretty Patterns Green Mamba RDRFrf. BDrub. UDD Anaconda LBBDRb. Fdl. Rd. Uf. RRu Christmas Cross u. FFUUl. RFFUUFFLru

Conclusion - Group theory is an integral part of the Rubik’s cube It is possible to solve a Rubik’s cube by reversing the operations done

Work Cited n n n n n http: //cubeland. free. fr/infos/ernorubik. htm ¨ Christopher Goudey 2001 -2003 http: //regentsprep. org/Regents/math/permut/Lperm. htm ¨ 1999 -2008 http: //regentsprep. org Oswego City School District Regents Exam Prep Center http: //www. wikipedia. org http: //www. daniweb. com/code/snippet 459. html http: //www. cs. princeton. edu/courses/archive/fall 06/cos 402/papers/korfrubik. pdf http: //www. dougmair. blogspot. com/ http: //match. stanford. edu/bump/newcube. pdf http: //www. geometer. org/rubik/group. pdf Joyner, David. Adventures in Group Theory. Baltimore: John Hopkins U P, 2002.

Acknowledgments Dr. Russell L. Herman n Mr. David B. Glasier n Mr. Nathaniel Jones n Mr. Doug Mair n Mr. Ernö Rubik n The SVSM Staff n
- Slides: 24