Mathematics and Implementation of Computer Graphics Techniques 2015
![Small differences from [Huang 11] • 13](https://slidetodoc.com/presentation_image_h2/a233ee62c9a2740db1245f78d4718cdf/image-13.jpg "Small differences from [Huang 11] • 13")
![Recent ar. Xiv paper [Ray & Sokolov 2015] • Unified view toward 2 D](https://slidetodoc.com/presentation_image_h2/a233ee62c9a2740db1245f78d4718cdf/image-14.jpg "Recent ar. Xiv paper [Ray & Sokolov 2015] • Unified view toward 2 D")
- Slides: 15
Mathematics and Implementation of Computer Graphics Techniques 2015 Boundary Aligned Smooth 3 D Cross-Frame Field Jin Huang, Yiying Tong, Hongyu Wei, Hujun Bao SIGGRAPH Asia 2011 Kenshi Takayama Assistant Prof @ National Insitute of Informatics takayama@nii. ac. jp 2 nd round 3 October 2015
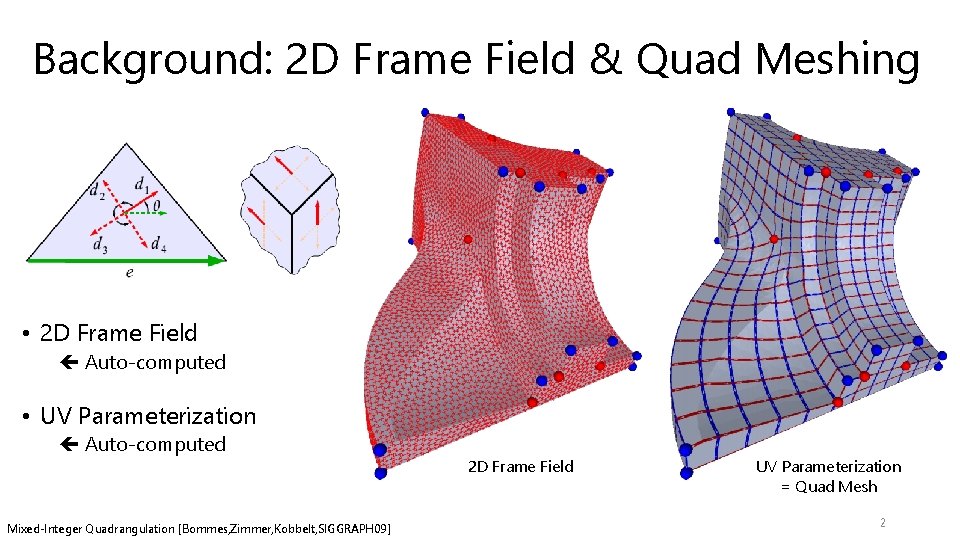
Background: 2 D Frame Field & Quad Meshing • 2 D Frame Field Auto-computed • UV Parameterization Auto-computed Mixed-Integer Quadrangulation [Bommes, Zimmer, Kobbelt, SIGGRAPH 09] 2 D Frame Field UV Parameterization = Quad Mesh 2
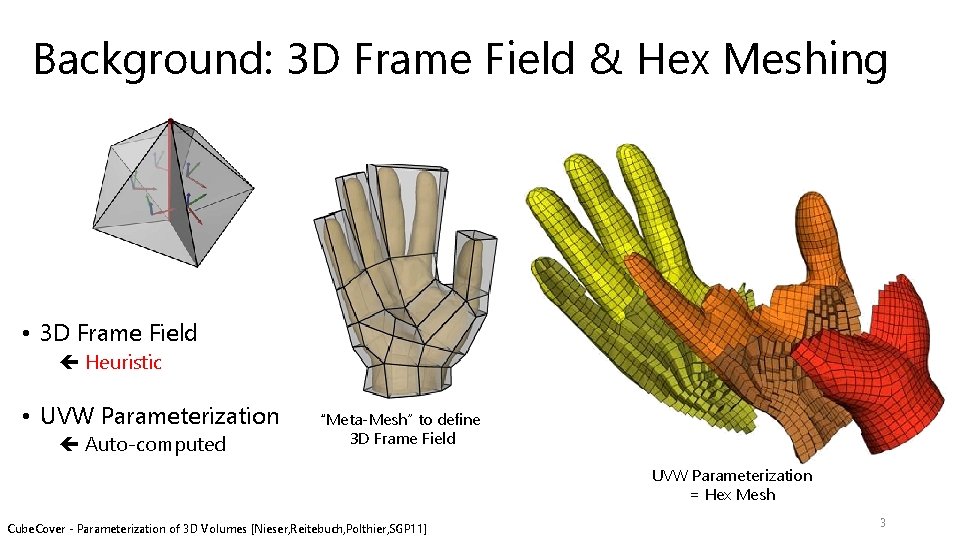
Background: 3 D Frame Field & Hex Meshing • 3 D Frame Field Heuristic • UVW Parameterization Auto-computed “Meta-Mesh” to define 3 D Frame Field UVW Parameterization = Hex Mesh Cube. Cover - Parameterization of 3 D Volumes [Nieser, Reitebuch, Polthier, SGP 11] 3
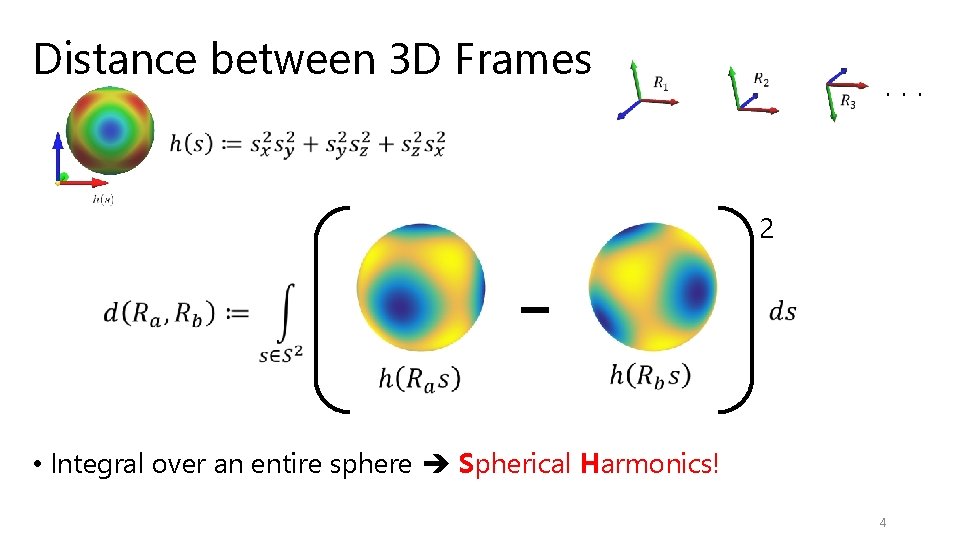
Distance between 3 D Frames ・・・ 2 • Integral over an entire sphere Spherical Harmonics! 4
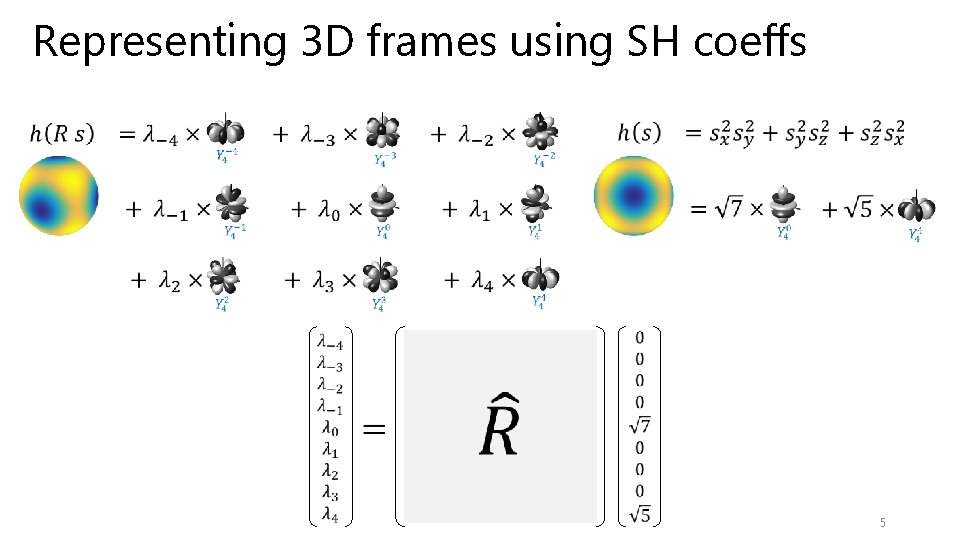
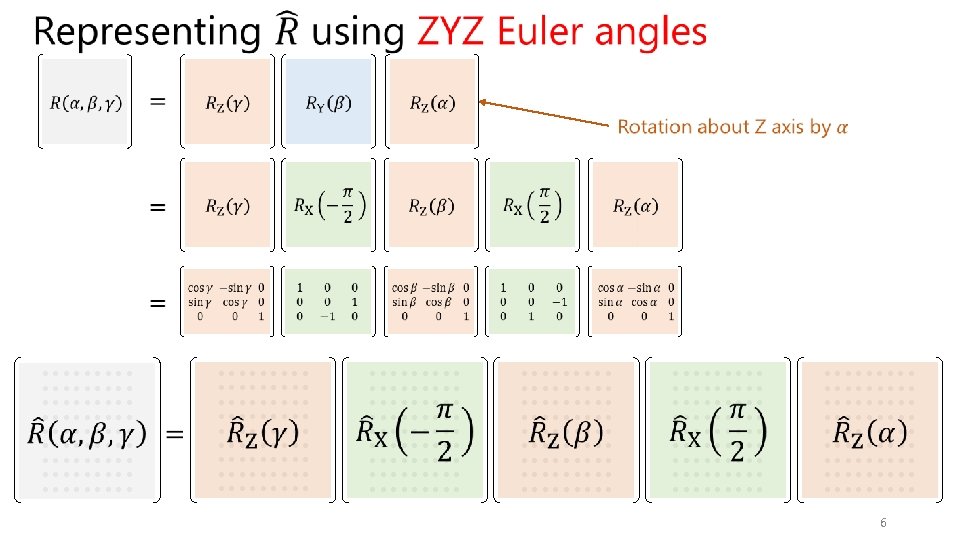
Representing 3 D frames using SH coeffs 5
https: //en. wikipedia. org/wiki/Table_of_spherical _harmonics#Real_spherical_harmonics use Computer Algebra Systems (CAS): Mathematica, Maple, Sage 7
Sage code (https: //cloud. sagemath. com) Y 4_4(x, y, z) = 3/4*sqrt(35/pi)*x*y*(x^2 - y^2) Y 4_3(x, y, z) = 3/4*sqrt(35/(2*pi))*(3*x^2 - y^2)*y*z Y 4_2(x, y, z) = 3/4*sqrt(5/pi)*x*y*(7*z^2 - 1) Y 4_1(x, y, z) = 3/4*sqrt(5/(2*pi))*y*z*(7*z^2 - 3) Y 40(x, y, z) = 3/16*sqrt(1/pi)*(35*z^4 - 30*z^2 + 3) Y 41(x, y, z) = 3/4*sqrt(5/(2*pi))*x*z*(7*z^2 - 3) Y 42(x, y, z) = 3/8*sqrt(5/pi)*(x^2 - y^2)*(7*z^2 - 1) Y 43(x, y, z) = 3/4*sqrt(35/(2*pi))*(x^2 - 3*y^2)*x*z Y 44(x, y, z) = 3/16*sqrt(35/pi)*(x^2 - 3*y^2) - y^2*(3*x^2 - y^2)) Y 4 = [Y 4_4, Y 4_3, Y 4_2, Y 4_1, Y 40, Y 41, Y 42, Y 43, Y 44] for i in range(9): v = [] for j in range(9): Si(theta, phi) = Y 4[i](sin(theta)*cos(phi+a), sin(theta)*sin(phi+a), cos(theta)) Sj(theta, phi) = Y 4[j](sin(theta)*cos(phi), sin(theta)*sin(phi), cos(theta)) v. append(integral(Si(theta, phi) * Sj(theta, phi) * sin(theta), theta, 0, pi). integrate(phi, 0, 2*pi)) print v for i in range(9): v = [] for j in range(9): Si(theta, phi) = Y 4[i](sin(theta)*cos(phi), -cos(theta), sin(theta)*sin(phi)) Sj(theta, phi) = Y 4[j](sin(theta)*cos(phi), sin(theta)*sin(phi), cos(theta)) v. append(integral(Si(theta, phi) * Sj(theta, phi) * sin(theta), theta, 0, pi). integrate(phi, 0, 2*pi)) print v
Matrices written down 9
Going between ZYZ (3 D) SH (9 D) • 10
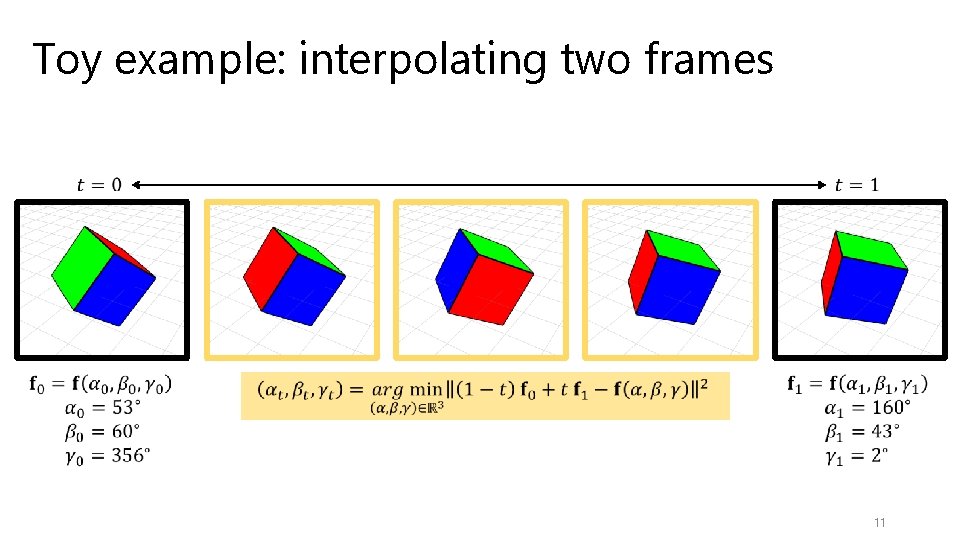
Toy example: interpolating two frames 11
Real examples with tetrahedral meshes 12
Small differences from [Huang 11] • 13
Recent ar. Xiv paper [Ray & Sokolov 2015] • Unified view toward 2 D & 3 D problems • Better handling of normal alignment • “Feasibility” constraint linearized & integrated into iterative solve • SH cookbook, concise pseudocode http: //arxiv. org/abs/1507. 03351 14
Small ideas for further improvements • Fix 3 D frames on boundary using 2 D frames • Decouple 9 SH coeffs x 1/9 dimensionality • Jacobi-style iteration simple & parallel • Other scattered-data-interpolation tools (RBF / MLS) ? • (Not my main focus anyway) Instant Field-Aligned Meshes [Jakob, Tarini, Panozzo, Sorkine-Hornung, SIGGRAPH Asia 2015] 15