Mathematics 40 S Applied Matrices Introduction Matrix mathematics










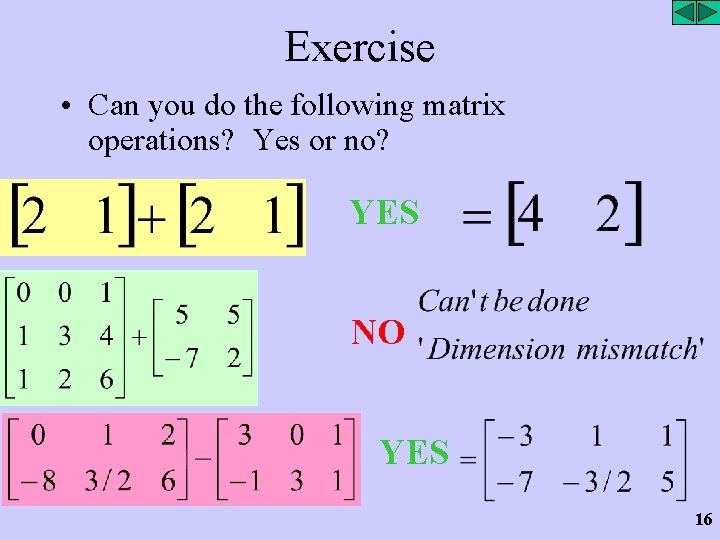













- Slides: 32

Mathematics 40 S Applied Matrices • Introduction: Matrix mathematics is a remarkably convenient and powerful method of manipulating large ‘arrays’ of organized numerical data. There is nothing magic about matrices, they are simply a means of expressing mathematically what you probably do in your head all the time. • Run this as an animated ‘slideshow’ Click the icon that looks like this: • Hit the space bar or left click with the mouse to accelerate the show. • Click the green arrows at the top right to advance slides or go back to a previous slide • Right click the mouse while animated for more advanced slide navigation features Build: 20090104 1

Introduction: A Familiar Array You put your three kids (Colleen, Nathan, and Dakota) to work every Sunday cleaning. Each gets a certain job: dusting, vacuuming, and doing bathrooms. The duration of each job is different. Last week the hours spent on jobs looked like this: This is just an ‘array’ of data: numbers arranged in an organized manner of rows and columns. Most mothers have these types of arrays in their head when deciding who is to do what household chores! 2

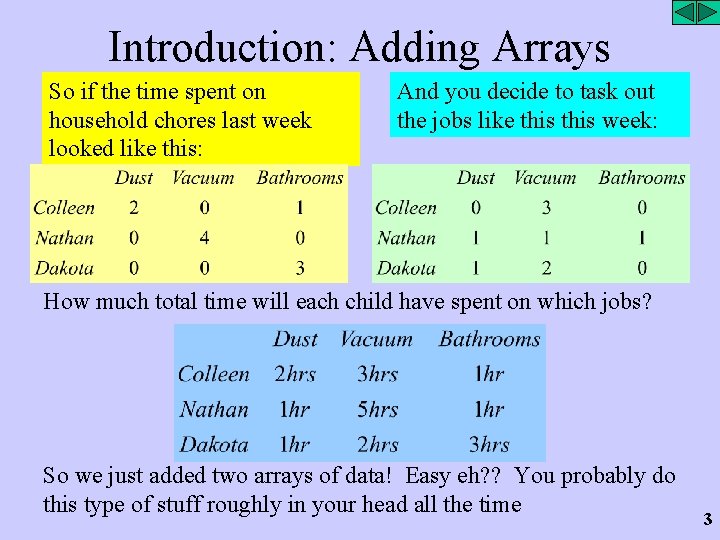
Introduction: Adding Arrays So if the time spent on household chores last week looked like this: And you decide to task out the jobs like this week: How much total time will each child have spent on which jobs? So we just added two arrays of data! Easy eh? ? You probably do this type of stuff roughly in your head all the time 3

Introduction: Simple Multiply What if the kids said they wanted to be paid for their work? ? Say you agree to two dollars per hour of work. How much would you pay them for the last two weeks? Here was the array of their work hours! Since every hour of each type of work gets $2 then the pay you would give the kids is: 4

Introduction: Complex Multiply Now what if the kids claim that doing dusting should only be worth $0. 50 per hour, vacuuming worth $2 per hour and bathrooms should be worth $3 per hour!!? ? How would you calculate that? Getting a bit more difficult! It works out their pay should be this! Work the kids did: Pay: But what if you had 10 kids (or 100 employees)? Wouldn’t it be nice to have a simple mathematical way to do these large numbers of simple calculations? There is! Using ‘MATRICES’ 5

Form of a Matrix A matrix is just the numerical elements of an array. We can only mathematically manipulate numbers, not names and jobs. But if we remember what each row stands for (Child) and what each column stands for (Job Hours) then we can make a MATRIX by putting square brackets around the numerical elements of the array. The table or array The Matrix 6

Characteristics of a Matrix Here is a typical matrix Each number in a matrix is called an element It has columns It has rows Matrices are enclosed in square brackets [ ] Row 1 Row 2 Column 1 Column 2 Column 3 7

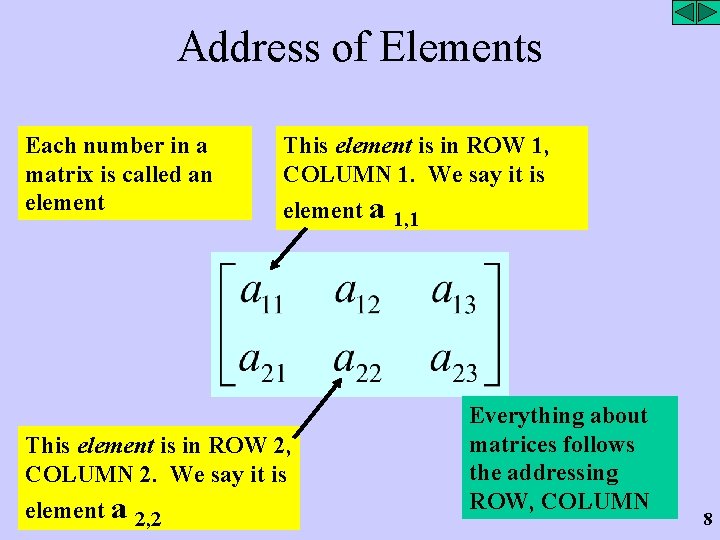
Address of Elements Each number in a matrix is called an element This element is in ROW 1, COLUMN 1. We say it is element a 1, 1 This element is in ROW 2, COLUMN 2. We say it is element a 2, 2 Everything Row, Column about matrices follows Row, Column the addressing Row, Column ROW, COLUMN 8

Dimension of a Matrix • We say a matrix has a ‘dimension’. Like saying its ‘size’ • The dimension is given as ROW x COLUMN • Here a 3 x 2 Matrix, or a Matrix A 3 x 2 It has 3 rows It has 2 columns We say matrix A is a ‘ 3 by 2’ matrix. Since it has a dimension of 3 rows by 2 columns. We can indicate just its dimension by saying A 3 x 2 9

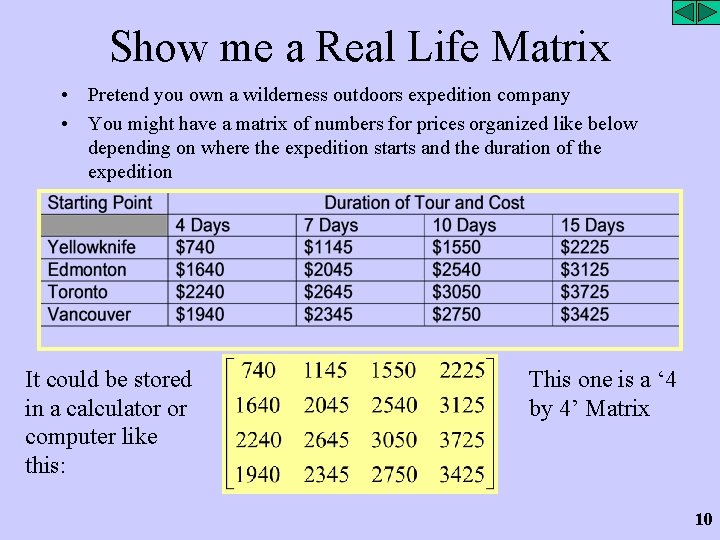
Show me a Real Life Matrix • Pretend you own a wilderness outdoors expedition company • You might have a matrix of numbers for prices organized like below depending on where the expedition starts and the duration of the expedition It could be stored in a calculator or computer like this: This one is a ‘ 4 by 4’ Matrix 10

Adding or Subtracting Matrices • Lets say you have your matrix for your wilderness expedition company; and you decide to increase every price by $100 on every package. Each matrix element increases by $100. It is just adding another matrix of numbers 11

Adding or Subtracting Matrices • To add or subtract matrices, the dimensions of both matrices must be the same. For example You can’t add a 2 by 3 matrix to a 3 by 2 matrix. 12

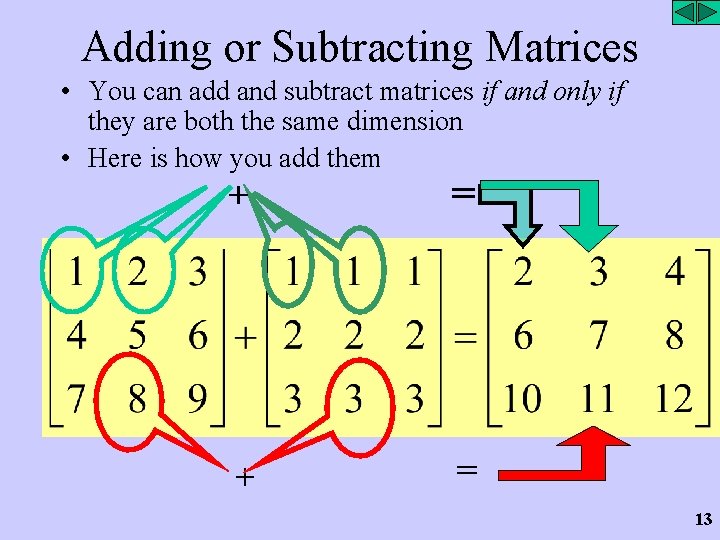
Adding or Subtracting Matrices • You can add and subtract matrices if and only if they are both the same dimension • Here is how you add them + = 13

Remember • You can only add or subtract matrices if they are the same dimension. Dimension is the number of rows and columns. • So for a Matrix A, of dimension Mx. N, and Matrix B of Dimension Px. Q, we can only add or subtract them if: # of Rows # of Columns M = P and N = Q to add or subtract!! In other words, they both must have the same number of rows and they both must have the same number of columns to add or subtract them 15
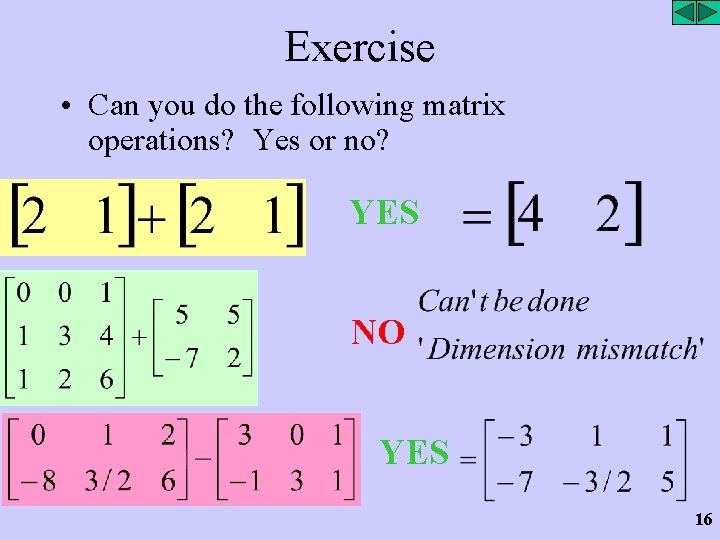
Exercise • Can you do the following matrix operations? Yes or no? YES NO YES 16

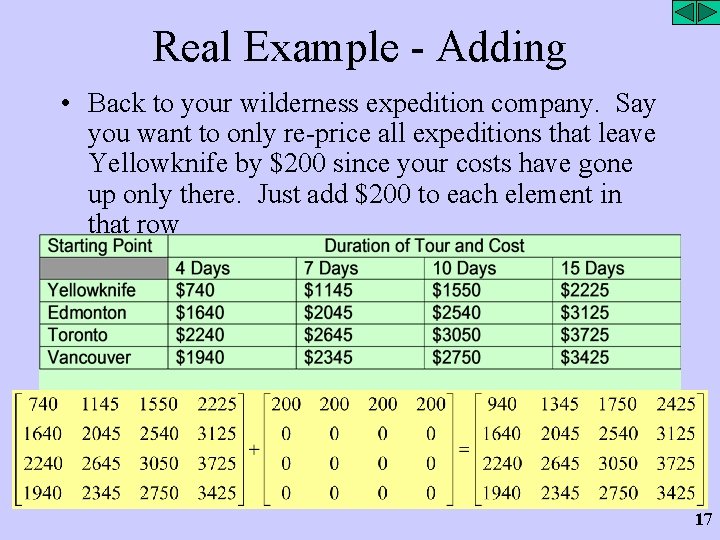
Real Example - Adding • Back to your wilderness expedition company. Say you want to only re-price all expeditions that leave Yellowknife by $200 since your costs have gone up only there. Just add $200 to each element in that row 17

Column and Row Matrices Column Matrices have only one column: Row Matrices have only one row: Square matrices have the same number of rows as columns: 18

Matrices on the TI-83 • The TI 83 Graphing Calculator handles matrices very well. • You will be given separate instructions on how to access the steps for using the TI 83 for matrices 19

Multiplying a Matrix by a ‘Scalar’ • A Scalar is just a constant multiplier. • It is possible to multiply each and every element of a matrix by a ‘scalar’ scalar constant To multiply by a • Say we have Matrix [M] scalar, every element of the matrix is multiplied by the scalar Or you could have just had three Ms added together, that is all multiplying means anyway! 20

Example – Multiply by Scalar • Let us look at our wilderness expedition company again. Say we want to calculate the GST (at 5%) for each tour package. The GST matrix would just look like this: This would be your GST matrix. You could add it to your pricing matrix if you want later 21

Multiplying Matrices • It is possible and also very powerful to multiply matrices by other matrices Multiplying matrices by matrices is a little complicated It is normally best done on IT (Integrated Technology) like a computer, EXCEL spreadsheet, or calculator 23

Matrices Dimensions - Multiplying To multiply matrices together the number of columns in the first matrix (the multiplicand matrix) must be the same as the number of rows in the second matrix (the multiplier matrix). Say we have two matrices A and B. A has dimensions M by N and B has dimensions P by Q. [A]Mx. N * [B]Px. Q The N must equal the P otherwise they can never be multiplied. In other words if the width of the first matrix isn’t the same as the height of the second matrix they can never be multiplied. The result of such multiplication is a matrix with dimensions M x Q 24

Dimensions and Matrix Multiplication Can the following be multiplied? And what is the Resultant matrix R if they can be? a. A 4 x 3 * B 3 x 1 Yes. Result is R 4 x 1 b. A 3 x 2 * B 2 x 5 c. A 4 x 3 * B 2 x 6 Yes. Result is R 3 x 5 No! 3 (Columns in A) is not equal to 2 (Rows in B) No! There are three columns in the first and only one row in the second d. 25

Properties of Multiplication of Matrices • Notice that given the rules about the allowed dimensions when multiplying that A*B may work, but B*A may not! • So matrix mathematics differs from normal math in that A*B is not necessarily the same a B*A if they can be even done at all. As a general rule; except under very fluky circumstances 26

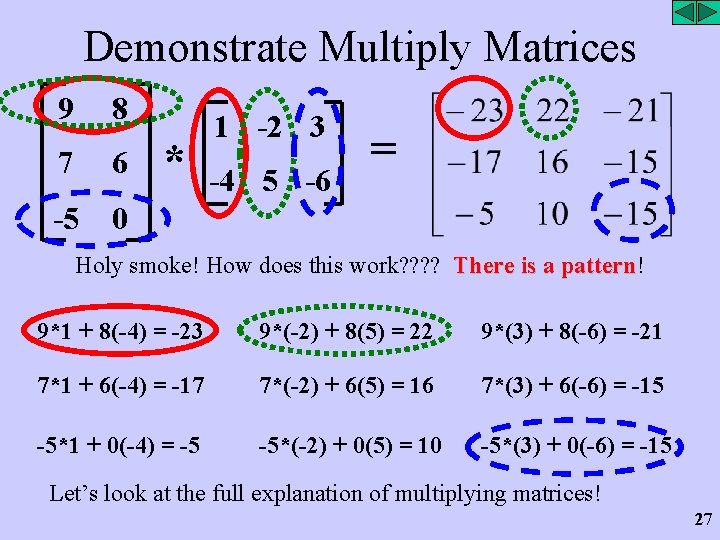
Demonstrate Multiply Matrices 9 8 7 6 -5 0 * 1 -2 3 -4 5 -6 = Holy smoke! How does this work? ? There is a pattern! pattern 9*1 + 8(-4) = -23 9*(-2) + 8(5) = 22 9*(3) + 8(-6) = -21 7*1 + 6(-4) = -17 7*(-2) + 6(5) = 16 7*(3) + 6(-6) = -15 -5*1 + 0(-4) = -5 -5*(-2) + 0(5) = 10 -5*(3) + 0(-6) = -15 Let’s look at the full explanation of multiplying matrices! 27

Multiply Matrices • If you have two matrices A and B and multiply them to get matrix R then: • To find element r 1, 1; find the product of a 1, 1 with element b 1, 1 and add the product of element a 1, 2 with element b 2, 1, etc until all the elements of row 1 of matrix A have been multiplied by all the elements in the columns of matrix B and their products added together. It is ‘row by column’ multiplying of the elements and adding of the products. What? ? 28

Multiplying Matrices with The TI-83 • Thankfully in Applied Math we just use our calculator to do the matrix multiplying! • So if you have difficulty with the full explanation on the previous slide, just make sure you are proficient with the calculator method. 29

Multiply Matrices Example 1 • Recall you paying your kids for household chores at the beginning of these notes? • Well how much you pay each child can be calculated using matrix multiplication Work in Hours Colleen gets 2 hrs at 50 cents plus 3 hours at $2 plus 1 hr at $3 so she gets $10. Nathan gets: etc… Pay per hour 30

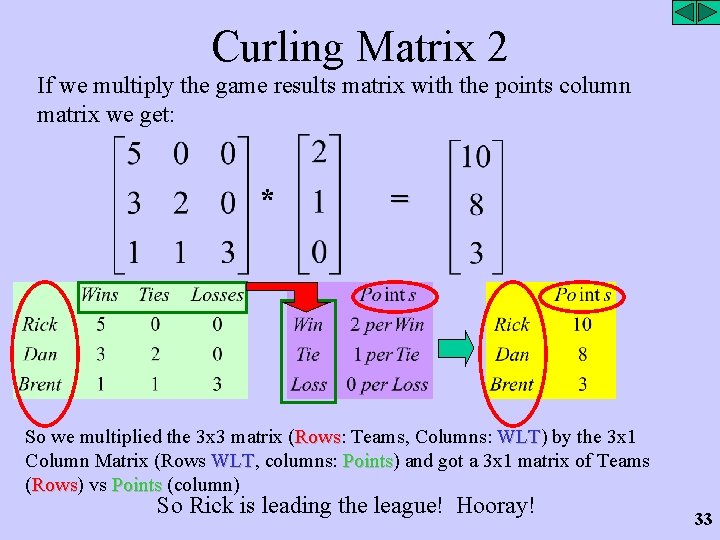
Multiply Matrices Example 2 • Let’s say you are the draw master (convener) for a curling league • The current game results look like this: Let’s say that a win is worth 2 points, a tie is worth 1 point and a loss is worth zero points Which team is the best? 31

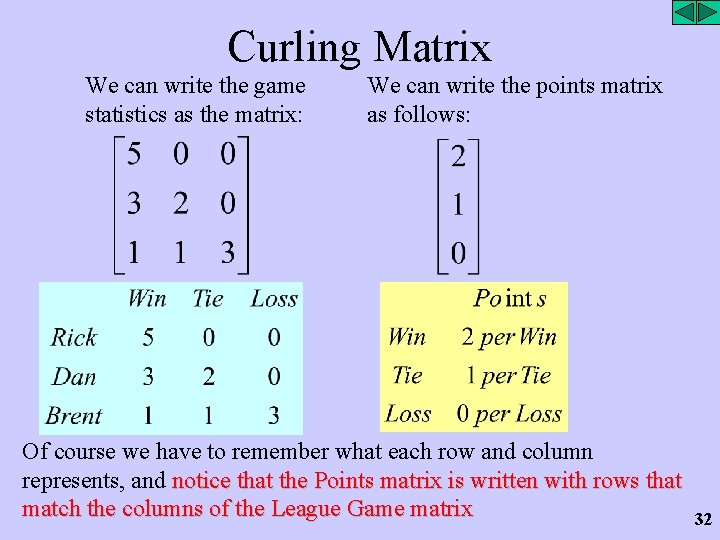
Curling Matrix We can write the game statistics as the matrix: We can write the points matrix as follows: Of course we have to remember what each row and column represents, and notice that the Points matrix is written with rows that match the columns of the League Game matrix 32

Curling Matrix 2 If we multiply the game results matrix with the points column matrix we get: * = So we multiplied the 3 x 3 matrix (Rows: Rows Teams, Columns: WLT) WLT by the 3 x 1 Column Matrix (Rows WLT, WLT columns: Points) Points and got a 3 x 1 matrix of Teams (Rows) Rows vs Points (column) So Rick is leading the league! Hooray! 33

Conclusion • So now you have the fundamentals of Matrices • They are very powerful! • And they are rather simple actually! • Matrices have lots of applications • We will learn only a few applications in Grade 12 Applied 34