Mathematical Structures of Belief Propagation Algorithms in Probabilistic

Mathematical Structures of Belief Propagation Algorithms in Probabilistic Information Processing Kazuyuki Tanaka Graduate School of Information Sciences, Tohoku University, Sendai, Japan http: //www. smapip. is. tohoku. ac. jp/~kazu/ 24 November, 2011 National Tsin Hua University, Taiwan 1

Contents 1. 2. 3. 4. 5. 6. 7. Introduction Bayesian Statistics Probabilistic Image Processing Gaussian Graphical Model Belief Propagation Various Applications of Probabilistic Information Processing Summary 24 November, 2011 National Tsin Hua University, Taiwan 2

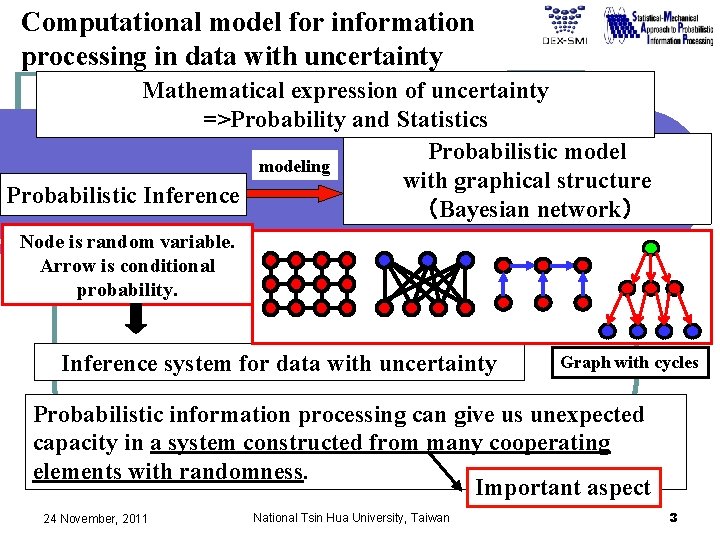
Computational model for information processing in data with uncertainty Mathematical expression of uncertainty =>Probability and Statistics Probabilistic modeling with graphical structure Probabilistic Inference （Bayesian network） Node is random variable. Arrow is conditional probability. Inference system for data with uncertainty Graph with cycles Probabilistic information processing can give us unexpected capacity in a system constructed from many cooperating elements with randomness. Important aspect 24 November, 2011 National Tsin Hua University, Taiwan 3

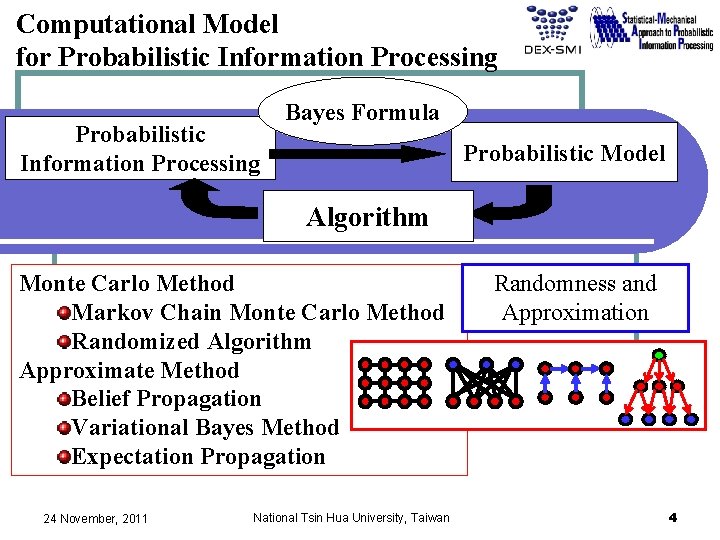
Computational Model for Probabilistic Information Processing Bayes Formula Probabilistic Model Algorithm Monte Carlo Method Markov Chain Monte Carlo Method Randomized Algorithm Approximate Method Belief Propagation Variational Bayes Method Expectation Propagation 24 November, 2011 National Tsin Hua University, Taiwan Randomness and Approximation 4

Contents 1. 2. 3. 4. 5. 6. 7. 24 November, 2011 Introduction Bayesian Statistics Probabilistic Image Processing Gaussian Graphical Model Belief Propagation Various Applications of Probabilistic Information Processing Summary National Tsin Hua University, Taiwan 5

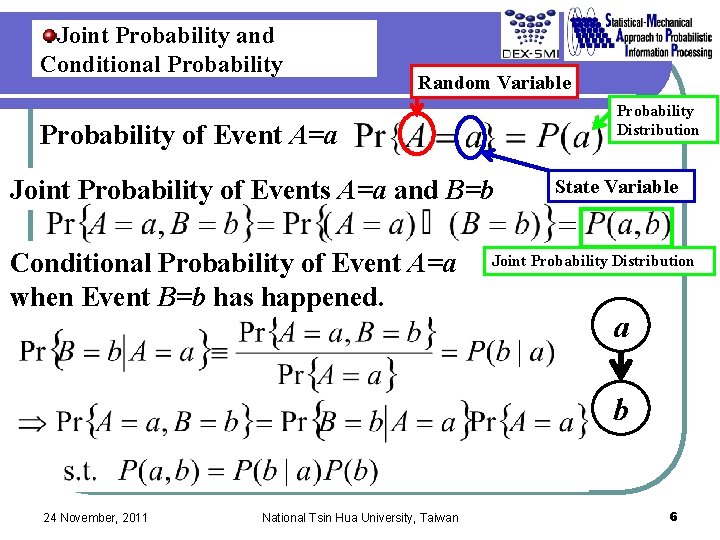
Joint Probability and Conditional Probability Random Variable Probability Distribution Probability of Event A=a Joint Probability of Events A=a and B=b Conditional Probability of Event A=a when Event B=b has happened. State Variable Joint Probability Distribution a b 24 November, 2011 National Tsin Hua University, Taiwan 6

Joint Probability and Independency of Events A and B are independent of each other In this case, the conditional probability can be expressed as 24 November, 2011 National Tsin Hua University, Taiwan a a b b 7

Marginal Probability Let us suppose that the sample space W is expressed by Ω= (A=0)∪ (A=1) ∪…∪ (A=M-1) where every pair of events is exclusive of each other. Graph with Two Nodes and One Edge a Marginal Probability of Event B=b in Joint Probability Pr{A=a, B=b} b Message = a b Marginalize Simplified Notation Summation over all the possible events in which every pair of events are exclusive of each other. 24 November, 2011 National Tsin Hua University, Taiwan 8

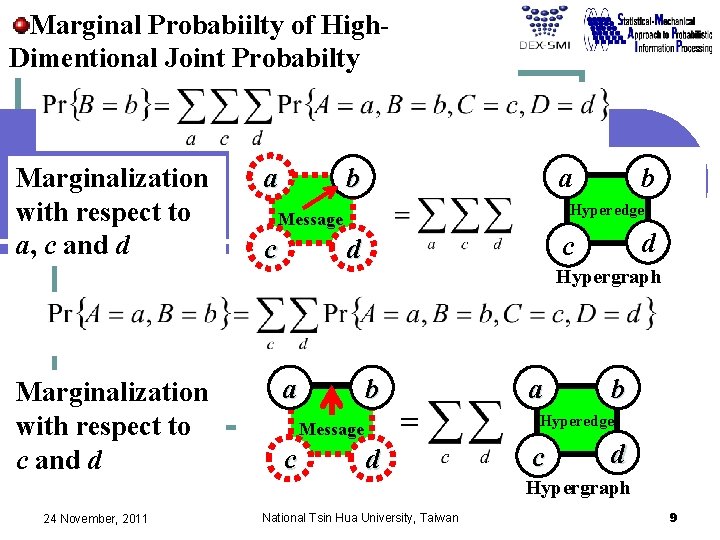
Marginal Probabiilty of High. Dimentional Joint Probabilty Marginalization with respect to a, c and d a b a Hyperedge Message c b d c d Hypergraph Marginalization with respect to c and d a b b Hyperedge Message c a d c d Hypergraph 24 November, 2011 National Tsin Hua University, Taiwan 9

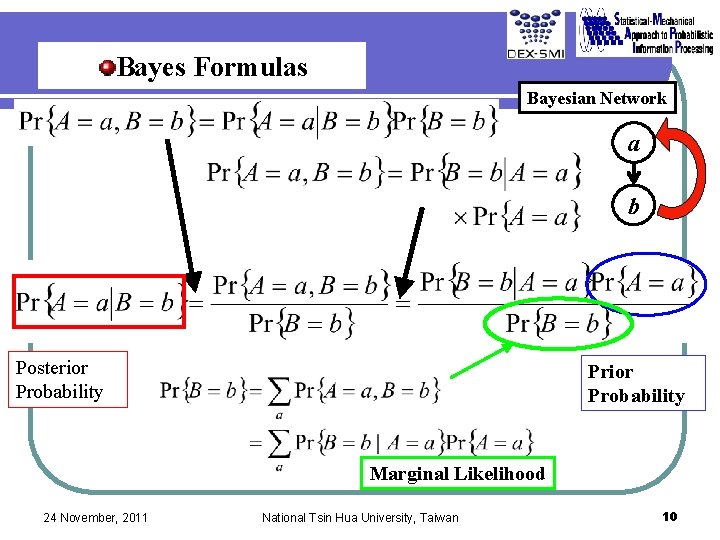
Bayes Formulas Bayesian Network a b Posterior Probability Prior Probability Marginal Likelihood 24 November, 2011 National Tsin Hua University, Taiwan 10

Contents 1. 2. 3. 4. 5. 6. 7. 24 November, 2011 Introduction Bayesian Statistics Probabilistic Image Processing Gaussian Graphical Model Belief Propagation Various Applications of Probabilistic Information Processing Summary National Tsin Hua University, Taiwan 11

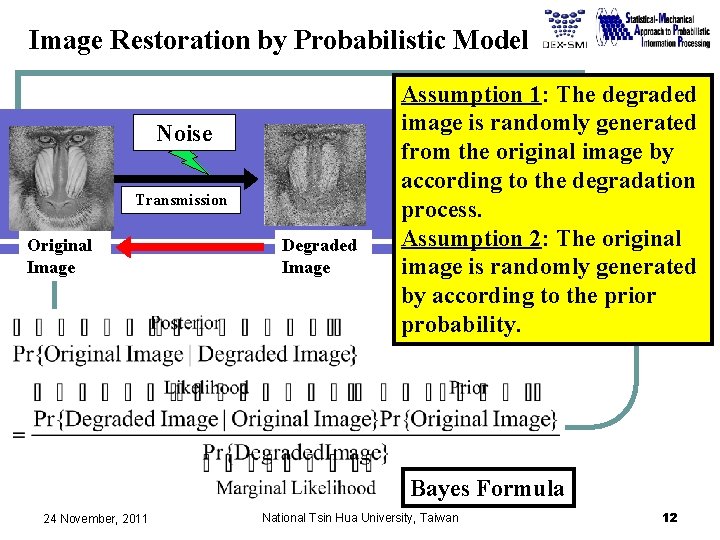
Image Restoration by Probabilistic Model Noise Transmission Original Image Degraded Image Assumption 1: The degraded image is randomly generated from the original image by according to the degradation process. Assumption 2: The original image is randomly generated by according to the prior probability. Bayes Formula 24 November, 2011 National Tsin Hua University, Taiwan 12

Prior Probability in Probabilistic Image Processing xi x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 24 November, 2011 x 12 xi xi xj xj State Variable of Light Intensity at i-th Pixel in Original Image National Tsin Hua University, Taiwan 13

Conditional Probability of Degradation Process Additive White Gaussian Noise xi y 1 X 1 y 2 X 2 y 5 X 5 xi X 3 y 6 X 6 y 9 X 9 y 3 X 4 y 7 X 7 y 10 X 10 y 4 y 8 X 8 y 11 X 11 y 12 yi State Variable of Light Intensity xi at i-th Pixel in Original Image State Variable of Light Intensity at i-th Pixel in yi Original Image X 12 yi 24 November, 2011 National Tsin Hua University, Taiwan 14

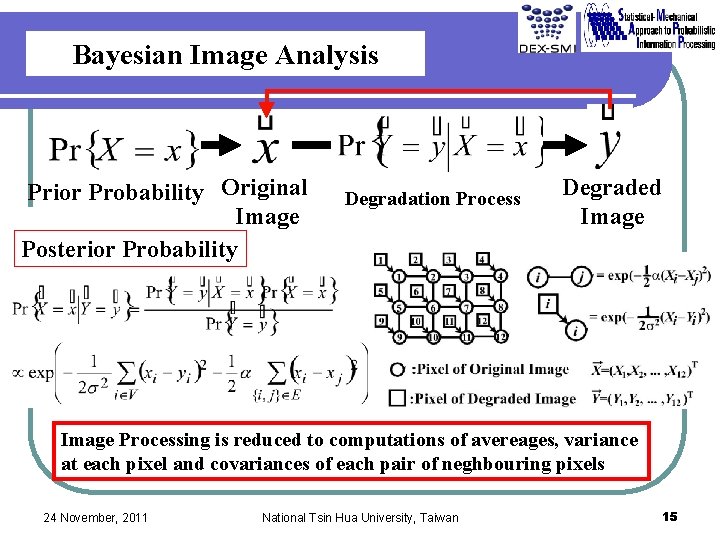
Bayesian Image Analysis Prior Probability Original Image Posterior Probability Degradation Process Degraded Image Processing is reduced to computations of avereages, variance at each pixel and covariances of each pair of neghbouring pixels 24 November, 2011 National Tsin Hua University, Taiwan 15

Statistical Estimation of Hyperparameters a, s are determined so as to maximize the marginal likelihood Pr{Y=y|a, s} with respect to a, s. EM (Expectation Maximization) Algorithm Original Image Degraded Image Marginalized with respect to X Marginal Likelihood 24 November, 2011 National Tsin Hua University, Taiwan 16

Contents 1. 2. 3. 4. 5. 6. 7. 24 November, 2011 Introduction Bayesian Statistics Probabilistic Image Processing Gaussian Graphical Model Belief Propagation Various Applications of Probabilistic Information Processing Summary National Tsin Hua University, Taiwan 17

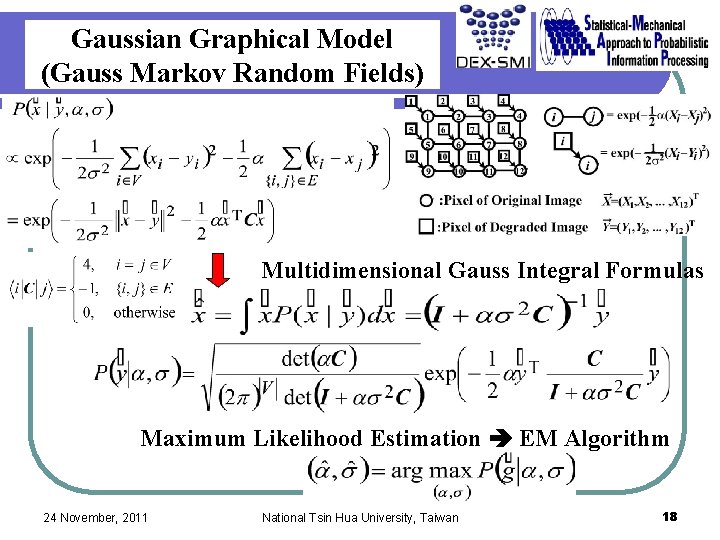
Gaussian Graphical Model (Gauss Markov Random Fields) Multidimensional Gauss Integral Formulas Maximum Likelihood Estimation EM Algorithm 24 November, 2011 National Tsin Hua University, Taiwan 18

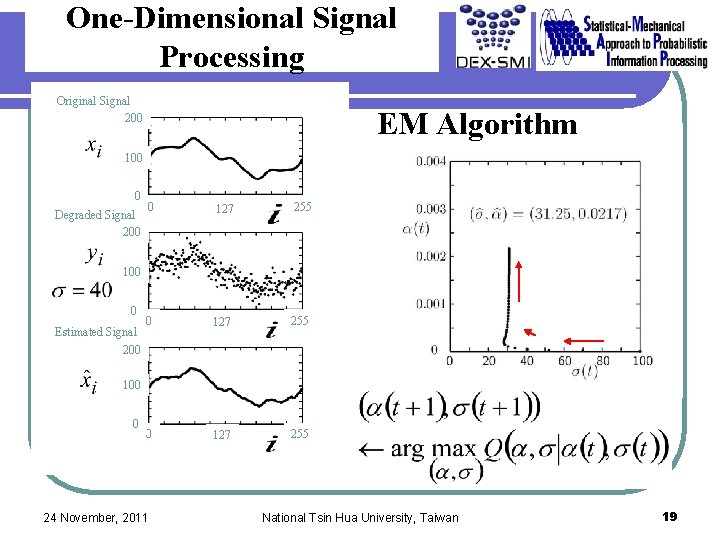
One-Dimensional Signal Processing Original Signal 200 EM Algorithm 100 0 Degraded Signal 200 0 127 255 100 0 Estimated Signal 200 100 0 24 November, 2011 National Tsin Hua University, Taiwan 19

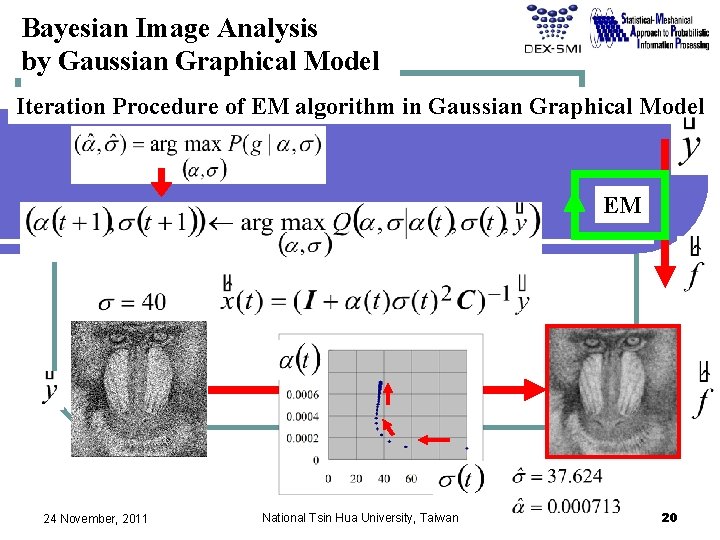
Bayesian Image Analysis by Gaussian Graphical Model Iteration Procedure of EM algorithm in Gaussian Graphical Model EM 24 November, 2011 National Tsin Hua University, Taiwan 20

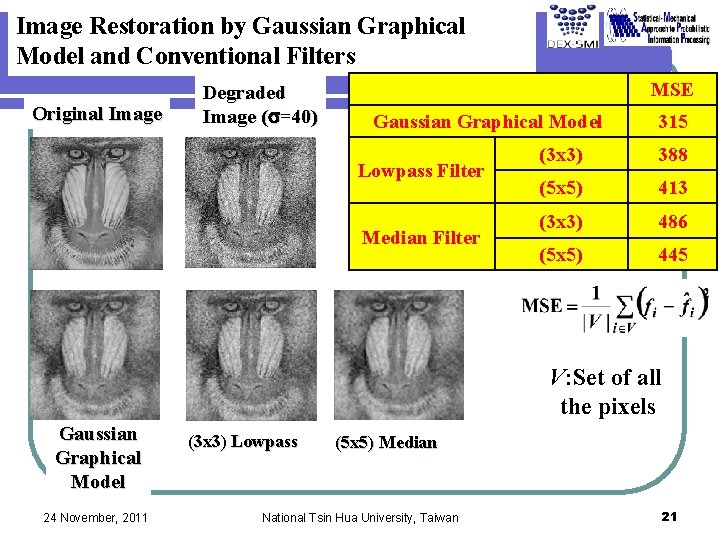
Image Restoration by Gaussian Graphical Model and Conventional Filters Original Image Degraded Image (s=40) MSE Gaussian Graphical Model Lowpass Filter Median Filter 315 (3 x 3) 388 (5 x 5) 413 (3 x 3) 486 (5 x 5) 445 V: Set of all the pixels Gaussian Graphical Model 24 November, 2011 (3 x 3) Lowpass (5 x 5) Median National Tsin Hua University, Taiwan 21

Contents 1. 2. 3. 4. 5. 6. 7. 24 November, 2011 Introduction Bayesian Statistics Probabilistic Image Processing Gaussian Graphical Model Belief Propagation Various Applications of Probabilistic Information Processing Summary National Tsin Hua University, Taiwan 22

What is an important point in computational complexity? How should we treat the calculation of the summation over 2 N configuration? If it takes 1 second in the case of N=10, it takes 17 minutes in N=20, 12 days in N=30 and 34 years in N=40. Markov Chain Monte Carlo Method Belief Propagation Method 24 November, 2011 National Tsin Hua University, Taiwan N fold loops This Talk 23

Strategy of Approximate Algorithm in Probabilistic Information Processing It is very hard to compute marginal probabilities exactly except some tractable cases. What is the tractable cases in which marginal probabilities can be computed exactly? Is it possible to use such algorithms for tractable cases to compute marginal probabilities in intractable cases? 24 November, 2011 National Tsin Hua University, Taiwan 24

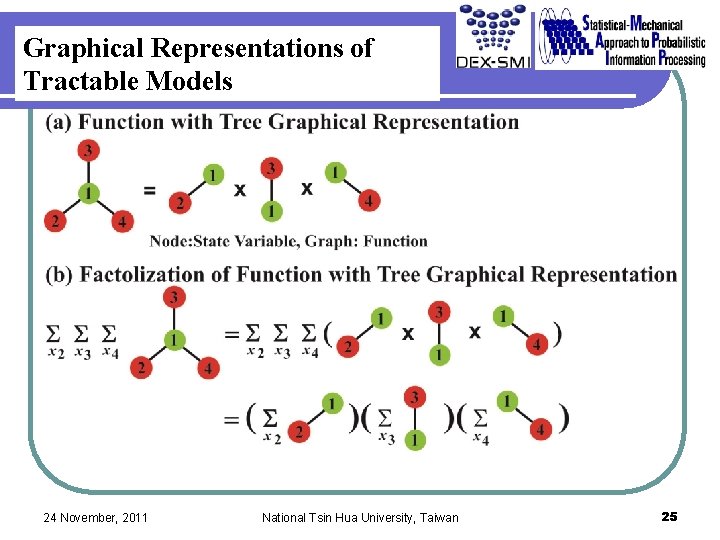
Graphical Representations of Tractable Models 24 November, 2011 National Tsin Hua University, Taiwan 25

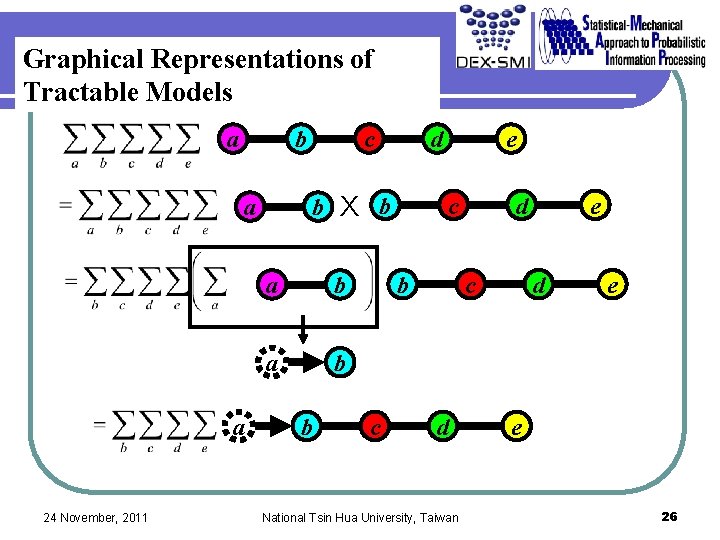
Graphical Representations of Tractable Models a b 24 November, 2011 d b X b a a c a b b e c b c d National Tsin Hua University, Taiwan e d e e 26

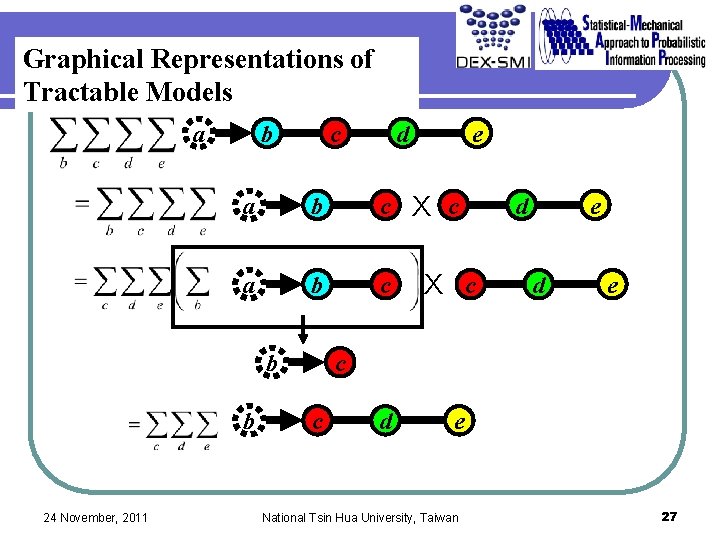
Graphical Representations of Tractable Models a b c e a b c X c a b c b b 24 November, 2011 d X c d e c c d e National Tsin Hua University, Taiwan 27

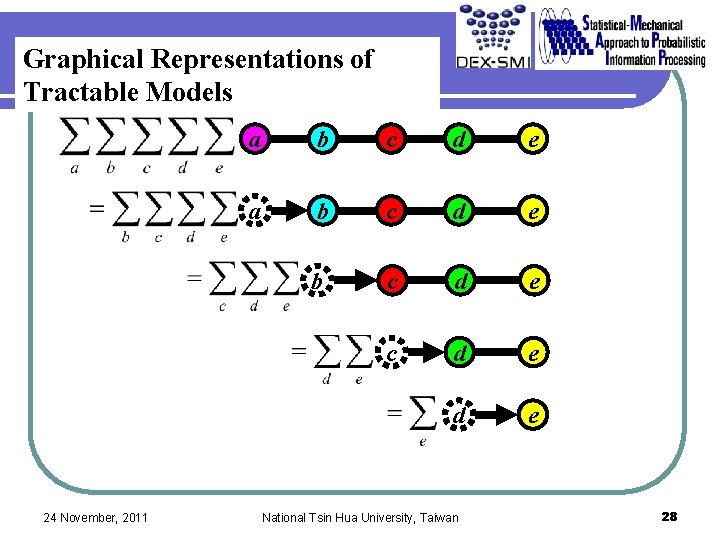
Graphical Representations of Tractable Models 24 November, 2011 a b c d e d e National Tsin Hua University, Taiwan 28

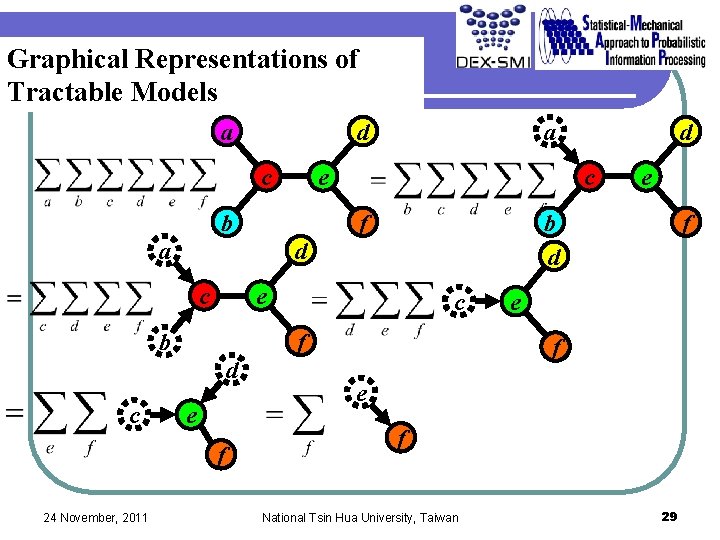
Graphical Representations of Tractable Models a d c f a e b e f 24 November, 2011 c f d e b d d c e b c a f e f National Tsin Hua University, Taiwan 29

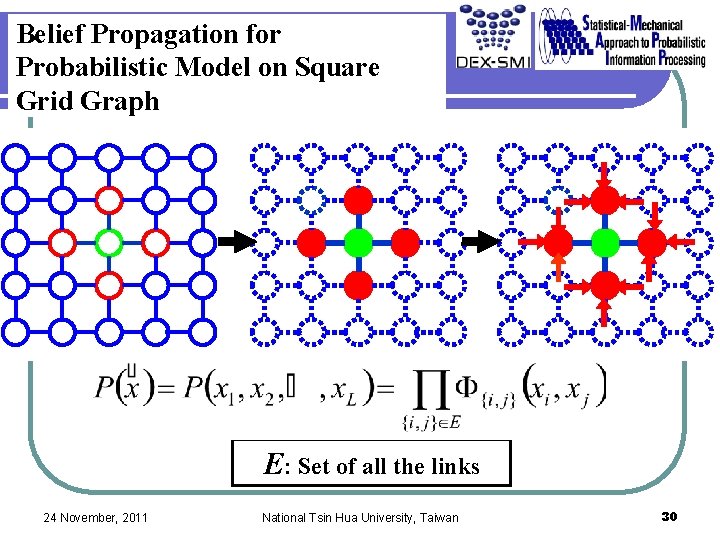
Belief Propagation for Probabilistic Model on Square Grid Graph E: Set of all the links 24 November, 2011 National Tsin Hua University, Taiwan 30

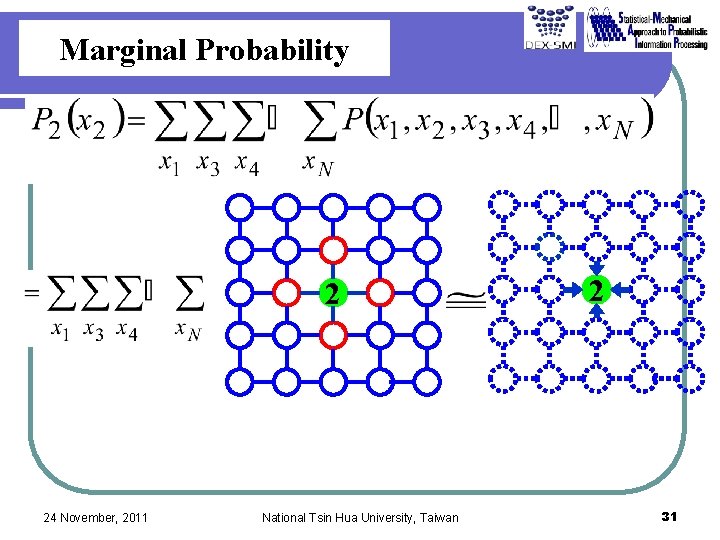
Marginal Probability 2 24 November, 2011 National Tsin Hua University, Taiwan 2 31

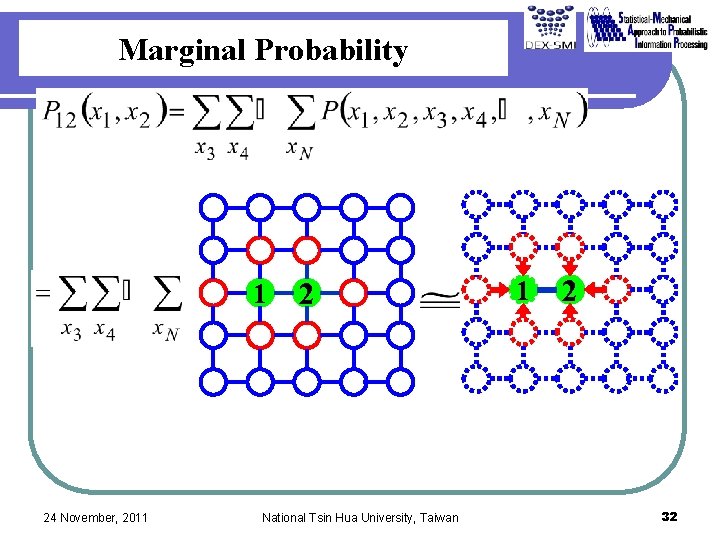
Marginal Probability 1 24 November, 2011 2 National Tsin Hua University, Taiwan 1 2 32

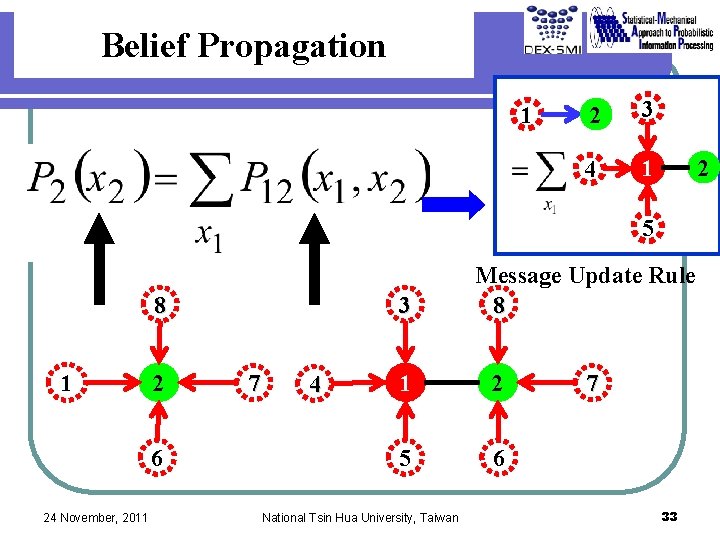
Belief Propagation 1 2 3 4 1 2 5 3 8 1 2 6 24 November, 2011 7 4 Message Update Rule 8 1 2 5 6 National Tsin Hua University, Taiwan 7 33

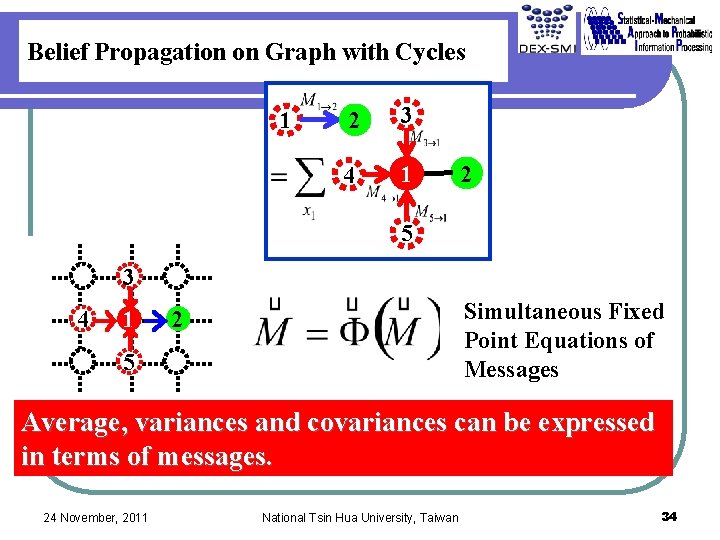
Belief Propagation on Graph with Cycles 1 2 3 4 1 2 5 3 4 1 Simultaneous Fixed Point Equations of Messages 2 5 Average, variances and covariances can be expressed in terms of messages. 24 November, 2011 National Tsin Hua University, Taiwan 34

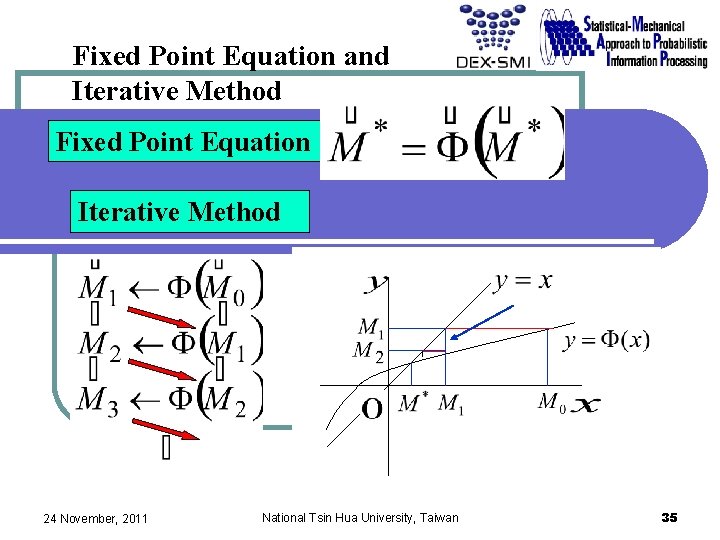
Fixed Point Equation and Iterative Method Fixed Point Equation Iterative Method 24 November, 2011 National Tsin Hua University, Taiwan 35

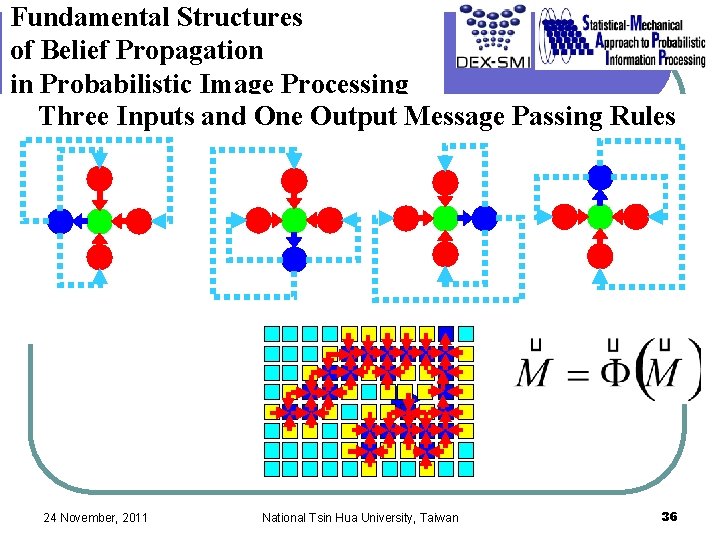
Fundamental Structures of Belief Propagation in Probabilistic Image Processing Three Inputs and One Output Message Passing Rules 24 November, 2011 National Tsin Hua University, Taiwan 36

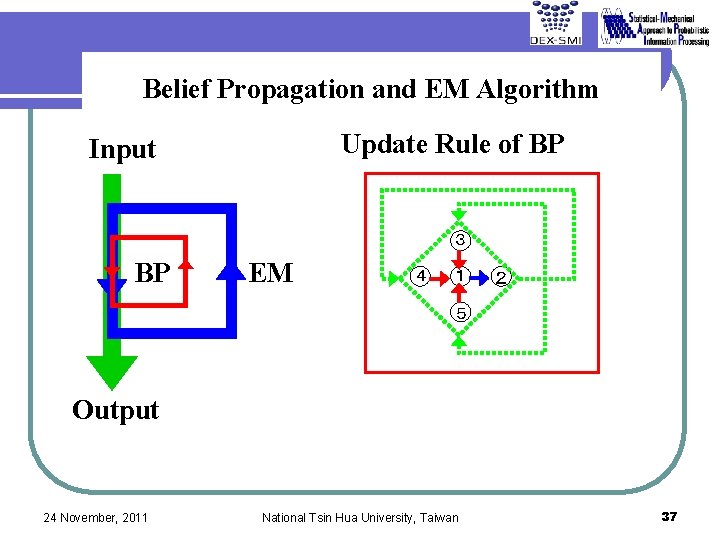
Belief Propagation and EM Algorithm Update Rule of BP Input ３ BP EM ４ １ ２ ５ Output 24 November, 2011 National Tsin Hua University, Taiwan 37

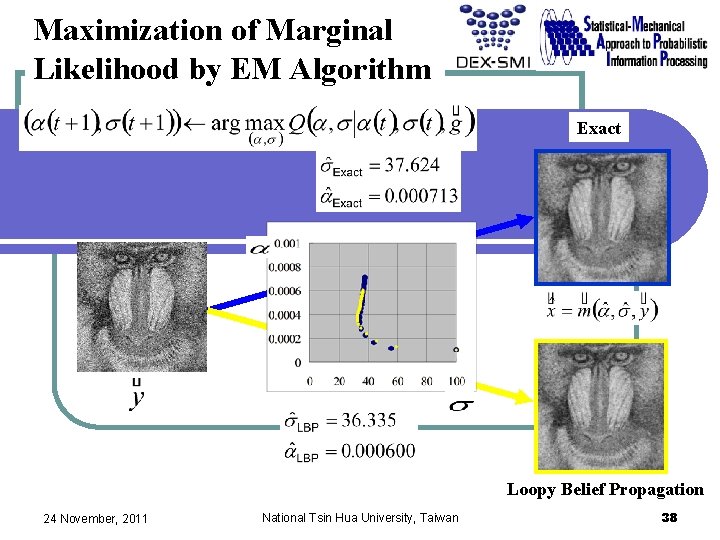
Maximization of Marginal Likelihood by EM Algorithm Exact Loopy Belief Propagation 24 November, 2011 National Tsin Hua University, Taiwan 38

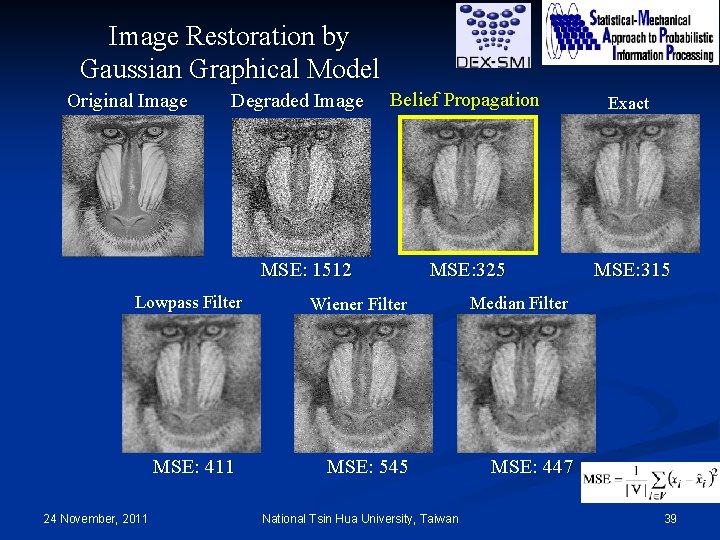
Image Restoration by Gaussian Graphical Model Original Image Degraded Image Belief Propagation Exact MSE: 325 MSE: 315 MSE: 1512 Lowpass Filter MSE: 411 24 November, 2011 Wiener Filter Median Filter MSE: 545 MSE: 447 National Tsin Hua University, Taiwan 39

Markov Random Fields Output Input Digital Images Inpainting based on MRF M. Yasuda, J. Ohkubo and K. Tanaka: Proceedings of CIMCA&IAWTIC 2005. 24 November, 2011 National Tsin Hua University, Taiwan 40

Contents 1. 2. 3. 4. 5. 6. 7. 24 November, 2011 Introduction Bayesian Statistics Probabilistic Image Processing Gaussian Graphical Model Belief Propagation Various Applications of Probabilistic Information Processing Summary National Tsin Hua University, Taiwan 41

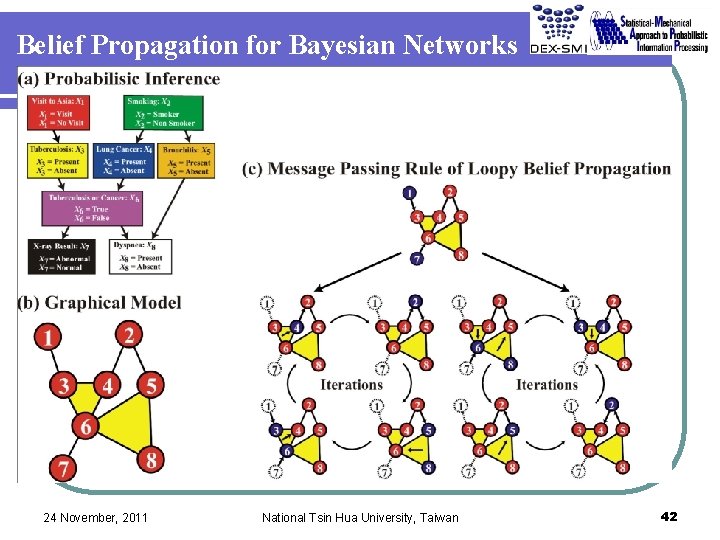
Belief Propagation for Bayesian Networks 24 November, 2011 National Tsin Hua University, Taiwan 42

Factor Graph Representations of Bayesian Networks and Belief Propagations 24 November, 2011 National Tsin Hua University, Taiwan 43

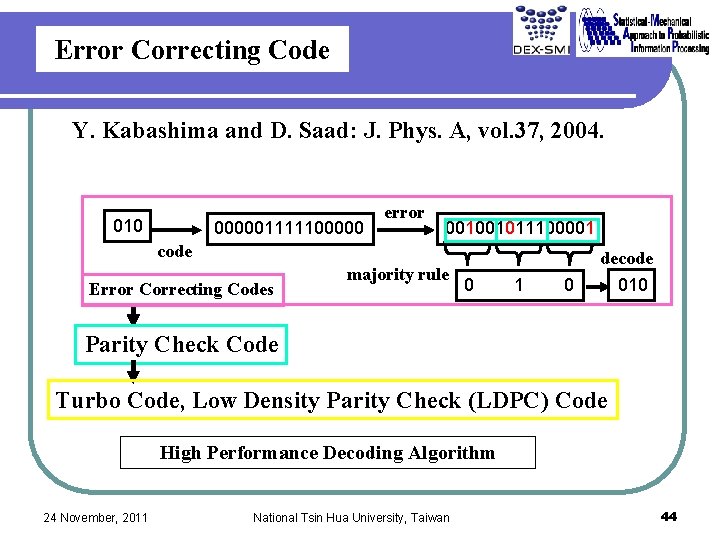
Error Correcting Code Y. Kabashima and D. Saad: J. Phys. A, vol. 37, 2004. 010 000001111100000 error 001001011100001 code Error Correcting Codes majority rule 0 1 0 decode 010 Parity Check Code Turbo Code, Low Density Parity Check (LDPC) Code High Performance Decoding Algorithm 24 November, 2011 National Tsin Hua University, Taiwan 44

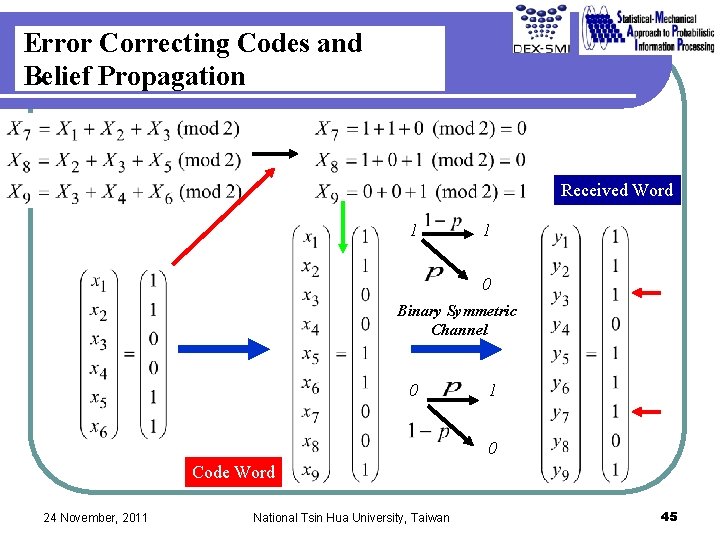
Error Correcting Codes and Belief Propagation Received Word 1 1 0 Binary Symmetric Channel 0 1 0 Code Word 24 November, 2011 National Tsin Hua University, Taiwan 45

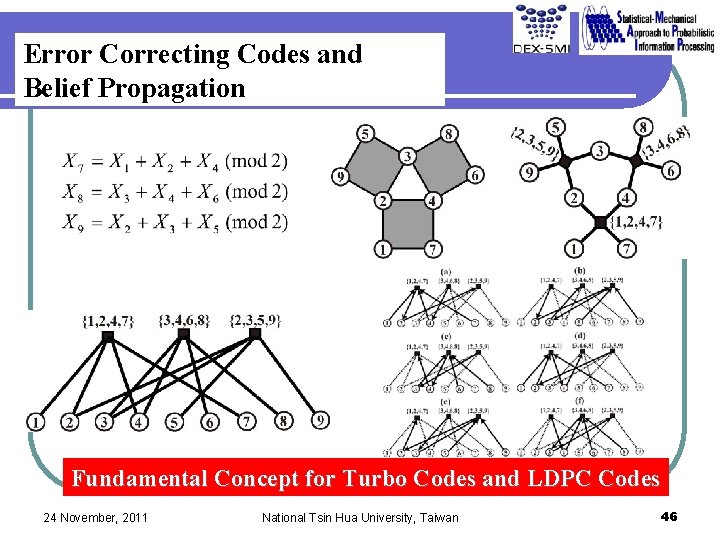
Error Correcting Codes and Belief Propagation Fundamental Concept for Turbo Codes and LDPC Codes 24 November, 2011 National Tsin Hua University, Taiwan 46

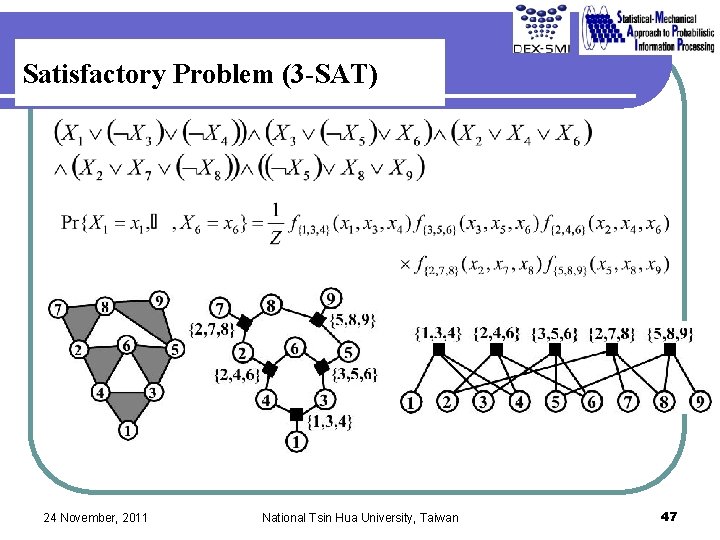
Satisfactory Problem (3 -SAT) 24 November, 2011 National Tsin Hua University, Taiwan 47

Contents 1. 2. 3. 4. 5. 6. 7. 8. 24 November, 2011 Introduction Bayesian Statistics Probabilistic Image Processing Gaussian Graphical Model Belief Propagation Statistical Performance Analysis Various Applications of Probabilistic Information Processing Summary National Tsin Hua University, Taiwan 48

Summary Fundamental Structures of Bayesian modeling have been introduced. Formulation of probabilistic image processing algorithms by means of loopy belief propagation has been summarized. Various applications of Bayesian Network Systems have been reviewed. 24 November, 2011 National Tsin Hua University, Taiwan 49

References 1. 2. 3. 4. 5. 6. K. Tanaka and D. M. Titterington: Statistical Trajectory of Approximate EM Algorithm for Probabilistic Image Processing, Journal of Physics A: Mathematical and Theoretical, vol. 40, no. 37, pp. 11285 -11300, 2007. M. Yasuda and K. Tanaka: The Mathematical Structure of the Approximate Linear Response Relation, Journal of Physics A: Mathematical and Theoretical, vol. 40, no. 33, pp. 9993 -10007, 2007. K. Tanaka and K. Tsuda: A Quantum-Statistical-Mechanical Extension of Gaussian Mixture Model, Journal of Physics: Conference Series, vol. 95, article no. 012023, pp. 1 -9, January 2008 K. Tanaka: Mathematical Structures of Loopy Belief Propagation and Cluster Variation Method, Journal of Physics: Conference Series, vol. 143, article no. 012023, pp. 1 -18, 2009 M. Yasuda and K. Tanaka: Approximate Learning Algorithm in Boltzmann Machines, Neural Computation, vol. 21, no. 11, pp. 3130 -3178, 2009. S. Kataoka, M. Yasuda and K. Tanaka: Statistical Performance Analysis in Probabilistic Image Processing, Journal of the Physical Society of Japan, vol. 79, no. 2, article no. 025001, 2010. 24 November, 2011 National Tsin Hua University, Taiwan 50

Textbooks Kazuyuki Tanaka: Introduction of Image Processing by Probabilistic Models, Morikita Publishing Co. , Ltd. , 2006 (in Japanese). Kazuyuki Tanaka: Mathematics of Statistical Inference by Bayesian Network, Corona Publishing Co. , Ltd. , 2009 (in Japanese). 24 November, 2011 National Tsin Hua University, Taiwan 51