Mathematical Relationship for Thin Lenses object do ho

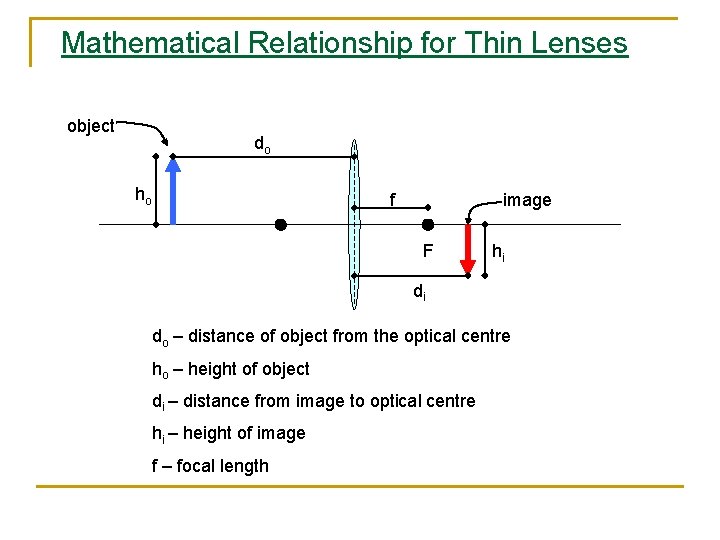
Mathematical Relationship for Thin Lenses object do ho f image F hi di do – distance of object from the optical centre ho – height of object di – distance from image to optical centre hi – height of image f – focal length

Sign Convention for Lenses Variable Positive do always never di real virtual image and object on opposite sides Image and object on same sides ho upright inverted hi upright inverted f converging diverging M upright Negative inverted

Magnification Equation

1. An object of height 8 cm is in front of a converging lens. An inverted real image of height 3 cm is produced. What is the magnification of the lens? ho = 8 cm hi = -3 cm M=? The magnification is -0. 375.

2. An object is 7 cm in front of a lens. An upright, virtual image of magnification 3 is noticed. Where is the image located? do = 7 cm M=3 di = ? The image is located 21 cm from the lens on the same side as the object.

Thin Lens Equation

1. A lens has a focal length of 17 cm. An object is located 48 cm from the lens. Where will the image be located and what type will it be? f = 17 cm do = 48 cm di = ? The image will be located 26. 3 cm from the lens and it will be real.

2. A diverging lens has a focal length of 29 cm. A virtual image is located 13 cm in front of the lens. Where is the object located? f = -29 cm di = -13 cm do = ? The object distance is 23. 6 cm.

3. A lens has a focal length of 3 cm. The object has a height of 4 cm and is located 5 cm from the lens. What is the location, height and type of image? (a) Use a ray diagram to find the characteristics. (b) Use a mathematical approach to find the characteristics.

S = -6 cm A = inverted L = 7. 5 cm T = real

f = 3 cm ho = 4 cm do = 5 cm di = ? hi = ?

The image has an inverted height of 6 cm and is located 7. 5 cm from the lens. The image is also real.