Mathematical Proof by Induction IB HL Using the

Mathematical Proof by Induction IB HL

Using the summation - example 1 Step i) Show that for n=1 the proof is true. Step ii) Assume that when n=k the proof is true. Assume Step iii) Now evaluate n=(k+1). Compare, the same, so proved. Step iv) Conclusion

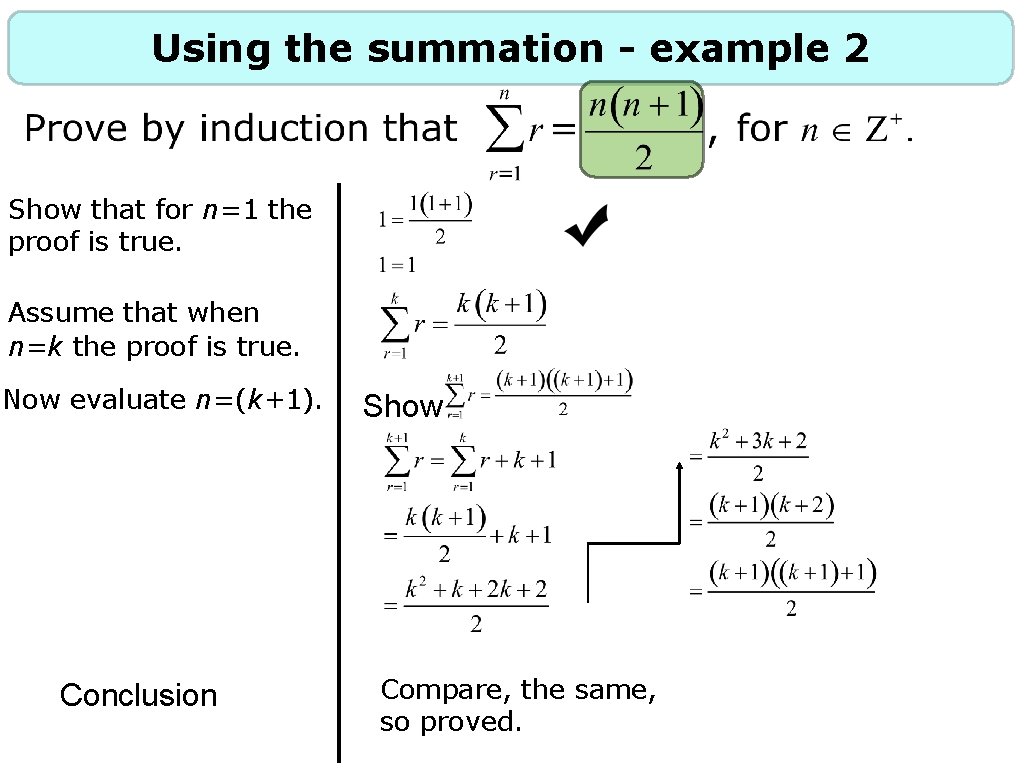
Using the summation - example 2 Show that for n=1 the proof is true. Assume that when n=k the proof is true. Now evaluate n=(k+1). Conclusion Show Compare, the same, so proved.

Using the summation - example 3 Show that for n=1 the proof is true. Assume that when n=k the proof is true. Assume Now evaluate n=(k+1). Show Conclusion Compare, the same, so proved.

Divisibility - example 1 Prove by induction that Show that for n=1 the proof is true. is divisible by 2, 2 is divisible by 2 Assume that when n=k the proof is true. We assume it is even which means there is some number p that when multiplied by 2 is our term. Now evaluate n=(k+1). Show: Is divisible by 2 Why do this? Conclusion Therefore: 2 is a factor for (k+1).

Divisibility - example 2 Prove by induction that Show that for n=1 the proof is true. 24 is divisible by 8 We assume it is divisible by 8 which means there is some number p that when multiplied by 8 is our term. Assume that when n=k the proof is true. Now evaluate n=(k+1). Conclusion is divisible by 8, Show Is divisible by 8 8 is a factor for (k+1).