Mathematical Models of Tonal Modulation and Application to

Mathematical Models of Tonal Modulation and Application to Beethoven‘s op. 106 Guerino Mazzola U & ETH Zürich Internet Institute for Music Science guerino@mazzola. ch www. encyclospace. org

Contents • A Modulation Model • Experiments with Beethoven • Generalizations • Open Questions

Model Arnold Schönberg: Harmonielehre (1911) Old Tonality Neutral Degrees (IC, VIC) Modulation Degrees (IIF, IVF, VIIF) New Tonality Cadence Degrees (IIF & VF) • What is the considered set of tonalities? • What is a degree? • What is a cadence? • What is the modulation mechanism? • How do these structures determine the modulation degrees?

Model 11 0 Space Z 12 of pitch classes in 12 -tempered tuning 1 2 10 C 9 3 8 Scale = part of Z 12 4 7 6 5 Twelve diatonic scales: C, F, Bb , Eb , Ab , Db , Gb , B, E, A, D, G

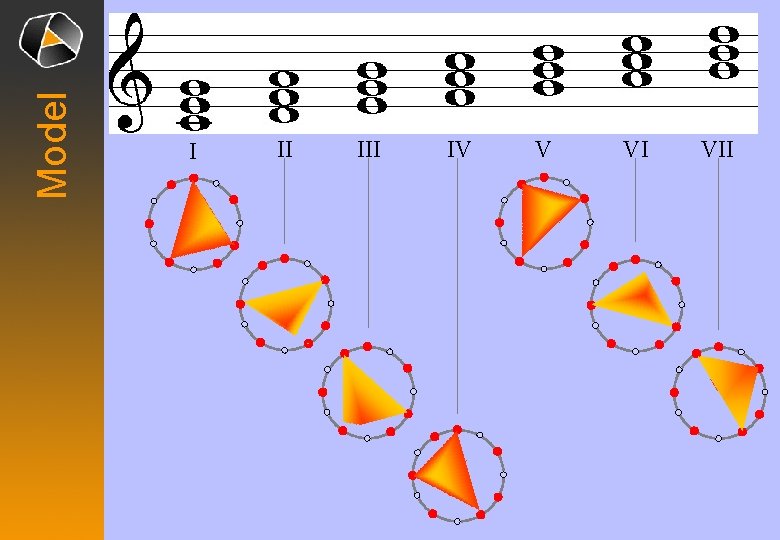
Model I II IV V VI VII

Model Harmonic strip of diatonic scale II VI V IV I VII III

Model C(3) G(3) F(3) Bb (3) Dia(3) A(3) E b(3) triadic coverings Ab(3) E(3) B(3) Db(3) Gb (3)

Model S(3) k 1(S(3)) = {IIS, VS} k 2(S(3)) = {IIS, IIIS} k 3(S(3)) = {IIIS, IVS} k 4(S(3)) = {IVS, VS} k 5(S(3)) = {VIIS} k k(S(3)) Space of cadence parameters

Model gluon W+ g strong force weak force electromagnetic force graviton gravitation quantum = set of pitch classes = M S(3) T(3) force = symmetry between S(3) and T(3) k k

et Model A et. A S(3) T(3) k et k modulation S(3) ® T(3) = „cadence + symmetry “

Model Given a modulation k, g: S(3) ® T(3) A quantum for (k, g) is a set M of pitch classes such that: • the symmetry g is a symmetry of M, g(M) = M • the degrees in k(T(3)) are contained in M • M Ç T is rigid, i. e. , has no proper inner symmetries • M is minimal with the first two conditions M S(3) T(3) g k k

Model Modulation Theorem for 12 -tempered Case For any two (different) tonalities S(3), T(3) there is • a modulation (k, g) and • a quantum M for (k, g) Further: • M is the union of the degrees in S(3), T(3) contained in M, and thereby defines the triadic covering M(3) of M • the common degrees of T(3) and M(3) are called the modulation degrees of (k, g) • the modulation (k, g) is uniquely determined by the modulation degrees.

IVC IIEb Model VIIEb IIC M(3) VC C(3) VIIC VE b IIIEb E b(3)

Ludwig van Beethoven: op. 130/Cavatina/# 41 Experiments Inversion e b : E b(3) ® B(3)

Ludwig van Beethoven: op. 130/Cavatina/# 41 Experiments Inversion e b : E b(3) ® B(3) b bb eb ab E b(3) g f Inversion e b B(3)

Ludwig van Beethoven: op. 106/Allegro/#124 -127 Experiments Inversiondb : G(3) ® E b(3) #124 - 125 #126 - 127 g db g

Ludwig van Beethoven: op. 106/Allegro/#188 -197 Generalization Catastrophe : E b(3) ® D(3)~ b(3)

Experiments Theses of Erwin Ratz (1973) and Jürgen Uhde (1974) Ratz: The „sphere“ of tonalities of op. 106 is polarized into a „world“ centered around B-flat major, the principal tonality of this sonata, and a „antiworld“ around B minor. Uhde: When we change Ratz‘ „worlds“, an event happening twice in the Allegro movement, the modulation processes become dramatic. They are completely different from the other modulations, Uhde calls them „catastrophes“. B-flat major B minor

Experiments Thesis: The modulation structure of op. 106 is governed by the inner symmetries of the diminished seventh chord C# -7 = {c#, e, g, bb} in the role of the admitted modulation forces. C(3) G(3) F(3) Bb (3) D(3) ~ b(3) E b(3) Ab(3) E(3) B(3) Gb (3) Db(3)

Generalization • All 7 -scales in well-tempered pitch classes -> Daniel Muzzulini/Hans Straub • Diatonic, melodic, and harmonic scales in just tuning -> Hildegard Radl • Applications to rhythmic modulation -> Guerino Mazzola • Ongoing research: Modulation for generalized tones -> Thomas Noll

Generalization Modulation Theorem for 12 -tempered 7 -tone Scales S and triadic coverings S(3) (Muzzulini) q-modulation = quantized modulation (1) S(3) is rigid. • For every such scale, there is at least one q-modulation. • The maximum of 226 q-modulations is achieved by the harmonic scale #54. 1, the minimum of 53 q-modulations occurs for scale #41. 1. (2) S(3) is not rigid. • For scale #52 and #55, there are q-modulations except for t = 1, 11; for #38 and #62, there are q-modulations except for t = 5, 7. All 6 other types have at least one quantized modulation. • The maximum of 114 q-modulations occurs for the melodic minor scale #47. 1. Among the scales with q-modulations for all t, the diatonic major scale #38. 1 has a minimum of 26.

Questions • Develop methodology and software for systematic experiments on given corpora of musical compositions (recognize tonalities and modulations thereof!) • Modulation in other musical dimensions, such as motive, rhythm, and global object spaces. • Modulation in other concept spaces for tonality and harmony, e. g. , self-addressed pitch, or harmonic topologies following Riemann. • Generalizing the quantum/force analogy in the modulation model, develop a general theory of musical dynamics, i. e. , theory of musical interaction forces between general structures.