Mathematical Models in Engineering and Science Mathematical Models

Mathematical Models in Engineering and Science.

Mathematical Models n (1) Formulate a real world situation in Mathematical terms. n This entails identifying relationships between variables and making assumptions about factors involved. n The end product is referred to as a MODEL. The mathematical model is likely to be realised in the form of an EQUATION. n n (2) Carry out a mathematical analysis on the model. Determine forecasts of outputs for particular inputs? n (3) Use the results of the mathematical analysis to forecast the outcome from the real world situation.

Mathematical modelling using Differential Equations. n n A differential equation is an equation which contains an unknown function and its derivative dy/dx. Differential equations are used to quantify many of the fundamental events in science and engineering, such as : a body falling in air with force F where F = ma = m(dv/dt) = mg-Bv. n n a voltage Vs across an inductive circuit where Vs = L(di) + i. R. dt a voltage Vs across a capacitive circuit where Vs = Vc + i. R = Q + R(d. Q). C dt

Differential equations n n n An ordinary differential equation is where there is only one independent variable, say i or Q to solve a differential equation INTEGRATE the expression to remove derivatives. So a differential equation of the form ( sinx = dy/dx - x 2) x is integrated term by term. Ie ∫dy = ∫(x + x 2 + sin x)dx , ie y = x 2/2 + x 3/3 – cosx + c The order of the differential equation depends upon the highest derivative. dy/dx = 3 y is first order, d 2 y/dx 2 - 6 dy/dx = 8 y is second order, d 3 y/dt 3 –td 2 t/dx 2 –y 2 = 0 is third order.

Case 1: A mass moving against friction. n n Friction Animation http: //www. bbc. co. uk/schools/scienceclips/age s/8_9/friction. shtml Total force FT = Force F 1 to accelerate body + Force F 2 to overcome friction. F 1 = ma = m(dv/dt) F 2 = Bv since kinetic friction depends upon velocity. m = mass, v = velocity, B = friction constant n So FT = F 1 + F 2 = m(dv) + Bv (1 st order diff eqn). dt

Case 2: A force absorbed by a spring and damper loaded mass. n n n Total force FT = Force F 1 to compress spring + Force F 2 absorbed by damper. Spri ng and damper compressed by distance x F 1 = kx ( Hookes Law) F 2 = Bv = B(dx/dt) since kinetic friction depends upon velocity. n So FT = F 1 + F 2 = B(dx) + kx. dt

Case 3: A body of mass m in free fall in air. n Total force FT = Force F 1 to accelerate body + Force F 2 to overcome friction in air. FT = mg ie free fall F 1 = ma = m(dv/dt) F 2 = Bv since kinetic friction depends upon velocity. n So FT = F 1 + F 2 = m(dv) + Bv. dt

Case 4: A current rising in an Inductor and Resistor circuit. n n n Resistance acts as a damper in RL circuits Upon Switch On the inductor opposes the rise of the current. The current then increases according to an exponential law. For a DC supply Vs = VL + VR = L(di) + i. R. . dt

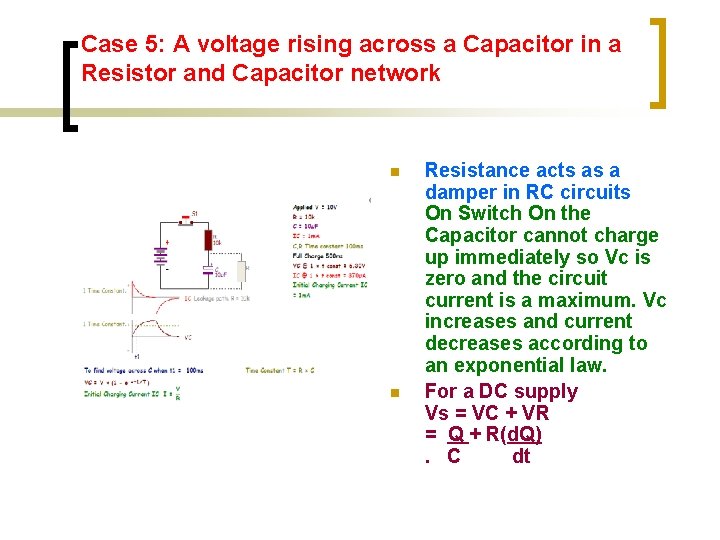
Case 5: A voltage rising across a Capacitor in a Resistor and Capacitor network n n Resistance acts as a damper in RC circuits On Switch On the Capacitor cannot charge up immediately so Vc is zero and the circuit current is a maximum. Vc increases and current decreases according to an exponential law. For a DC supply Vs = VC + VR = Q + R(d. Q). C dt

Mathematical Models: Conclusion n n Differential equations in mathematics can be formed to model behaviour of components and systems in Engineering and Science. End