Mathematical Magic tricks Michael Lambrou aria Drakaki There

Mathematical Magic tricks Michael Lambrou Μaria Drakaki

There is a fascinating relationship between magic and mathematics and a lot of hidden history behind magic tricks.

His work Introduction to Arithmetic was the standard arithmetic text for more than 1000 years. Nicomachus of Gerasa (~100 A. D. )

The work contains the first multiplication table in a Greek text.

In this work he describes a method by which we guess a number that someone has thought of: Think of a number from 1 to 100. Give me the remainders A, B, C when it is divided by 3, by 5 and by 7. I can tell you the number you are thinking. Method: calculate mod 105 the number 70 A + 21 B + 15 C

For example, suppose someone has thought of the number 19: 19=6 x 3+1 so, the remainder A = 1 19=3 x 5+4 B = 4 19=2 x 7+5 and C = 5 We calculate: 70 A + 21 B + 15 C = 70+84+75 = 229=2 x 105+ 19

Leonardo Fibonacci (1170 – 1250) Liber abaci (1202) In the eighth part of the twelfth chapter of this amazing manuscript we find that Fibonacci has a version of the three-object divination. It’s a typical math trick, perhaps suitable for a class of school children but far from performable for modern audiences. All of the tricks that Fibonacci describes have this flavor. Fibonacci was trying to teach people arithmetic, not magic.

The first printed magic book – with mathematical tricks - came out 1584 in Lyon. I. Prevost, La Première partie des subtiles et plaisantes inventions. It tries to teach magic in some detail—effects, methods, all described in a leisurely fashion. Prevost describes two versions of the Miracle Divination. (a coin trick) There are fewer than ten known copies of the book extant;

The next French book to appear is filled with mathematical tricks. Problèmes plaisants et délectables, Lyons 1624 Claude Gaspard Bachet de Méziriac (1581 -1638)

Examples of mathematical magic tricks

Think of a number from 10 to 99 and add its digits. Then subtract that sum from your number.

The explanation Suppose, you have thought of the number 32. 3+2=5 and 32 -5=27. I am sure that you have found a multiple of 9. 32=3 x 10 + 2 x 1 -3 -2 9 x 3 0

Generally: If ab is a 2 digit number, then ab=10 a+b Sum of its digits: a+b We subtract: 10 a+b-(a+b)= 9 a

The sum of the picked numbers is … 9 8 11 7 13 12 15 11 8 7 10 6 10 9 12 8 Pick a number and then delete all others in the same row or column. Repeat as much as you can. Sum=39
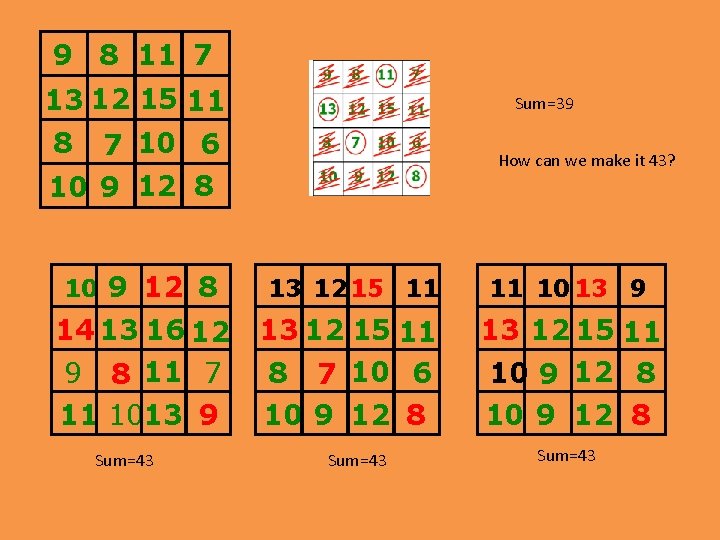
9 8 11 7 13 12 15 11 Sum=39 7 10 6 10 9 12 8 8 How can we make it 43? 10 9 12 8 13 12 15 11 11 10 13 9 14 13 16 12 9 8 11 7 13 12 15 11 8 7 10 6 13 12 15 11 10 9 12 8 11 1013 9 10 9 12 8 Sum=43
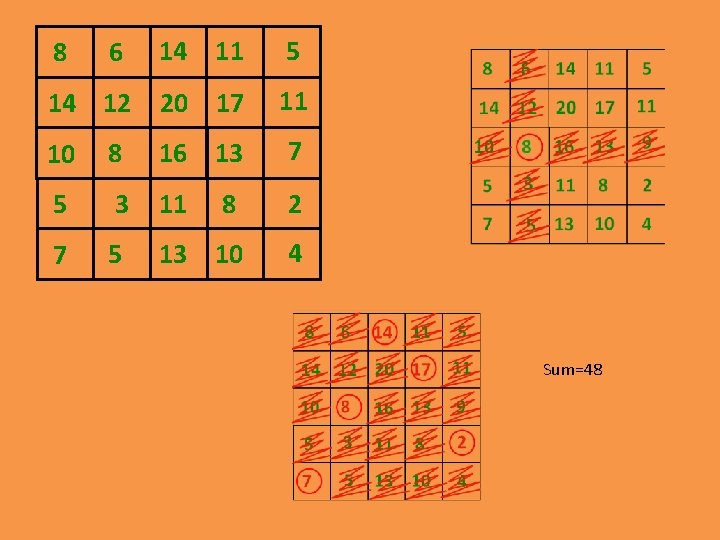
8 6 14 12 14 11 5 20 17 11 10 8 16 13 7 5 3 11 8 2 7 5 13 10 4 Sum=48
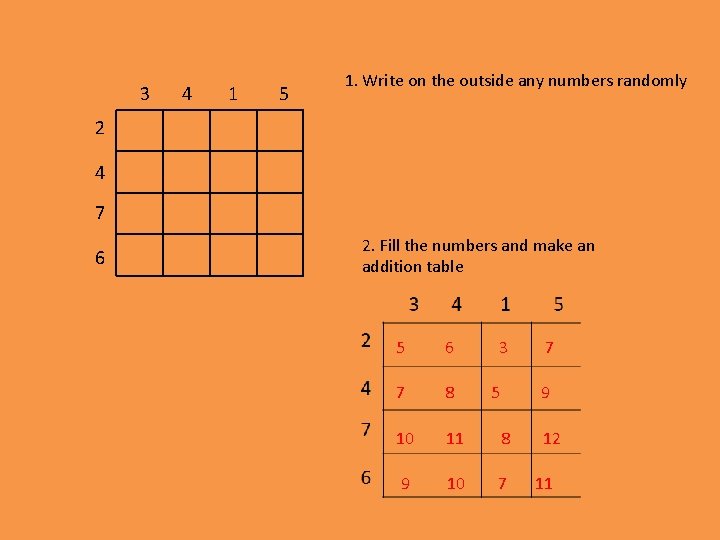
3 4 1 5 1. Write on the outside any numbers randomly 2 4 7 6 2. Fill the numbers and make an addition table 5 6 3 7 8 10 11 8 9 10 7 5 7 9 12 11
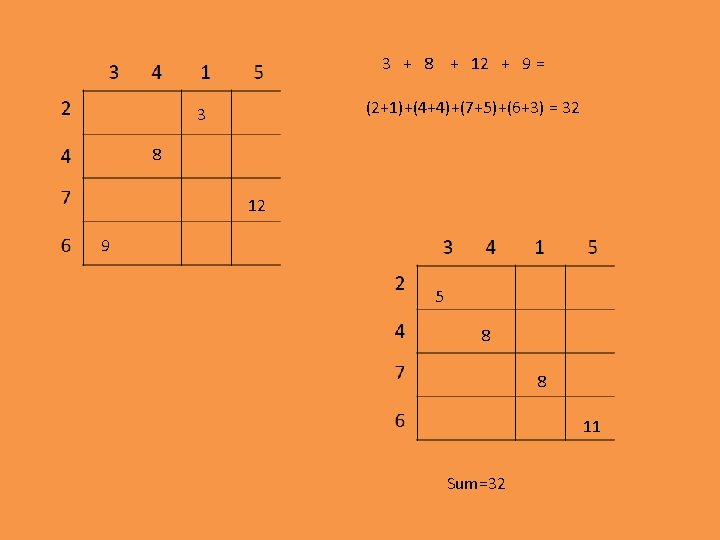
3 + 8 + 12 + 9 = (2+1)+(4+4)+(7+5)+(6+3) = 32 3 8 12 9 5 8 8 11 Sum=32
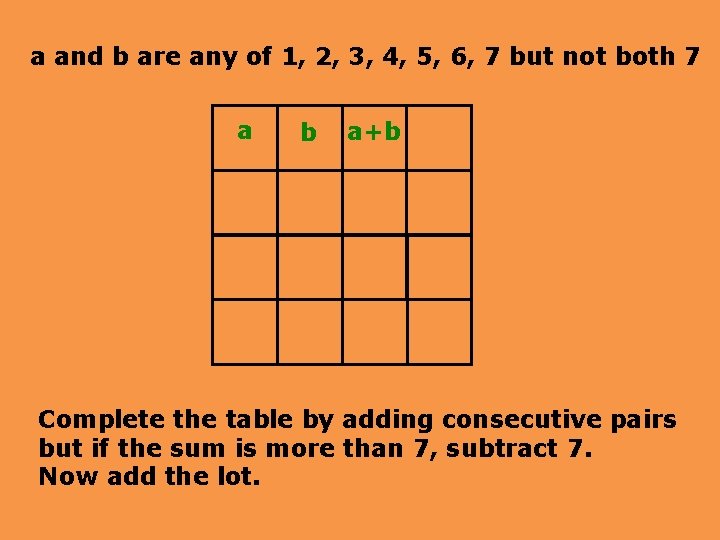
a and b are any of 1, 2, 3, 4, 5, 6, 7 but not both 7 a b a+b Complete the table by adding consecutive pairs but if the sum is more than 7, subtract 7. Now add the lot.

The sum you found should be 63. Why? Periodicity comes into it. There are three possible cycles of pairs, all adding to 63 1, 2, 3, 5, 1, 6, 7, 6, 6, 5, 4, 2, 6, 1, 7, 1, 1, 2 1, 3, 4, 7, 4, 4, 1, 5, 6, 4, 3, 7, 3, 3, 6, 2, 1, 3 1, 4, 5, 2, 7, 2, 2, 4, 6, 3, 2, 5, 7, 5, 5, 3, 1, 4

Magic sum 5 1 4 3 8 9 4 3 7 2 3 9 5 6 1 6 2 7 4 3 1 7 4 5 6 8 3 2 9 5
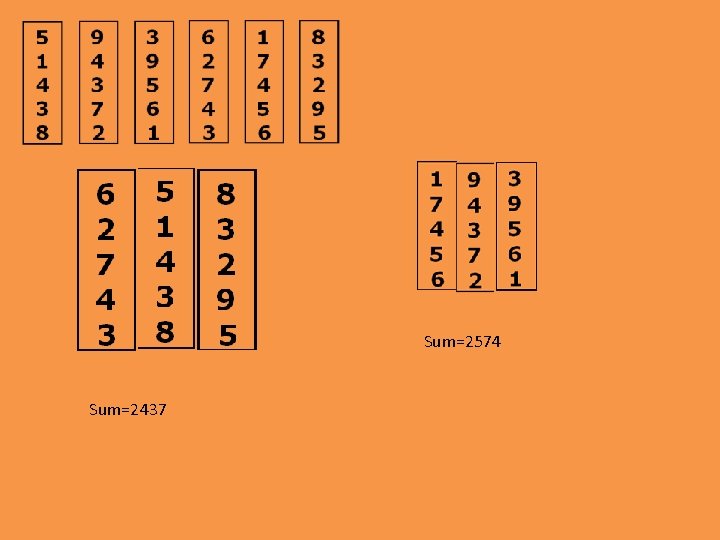
Sum=2574 Sum=2437

6+2+7+4+3=22 5+1+4+3+8=21 8+3+2+9+5=27 9 -2 2 4 3 4 -2+2 3 -2+2 7 20<Sum<30

Make your own cards with 7 numbers, whose sum is 40+
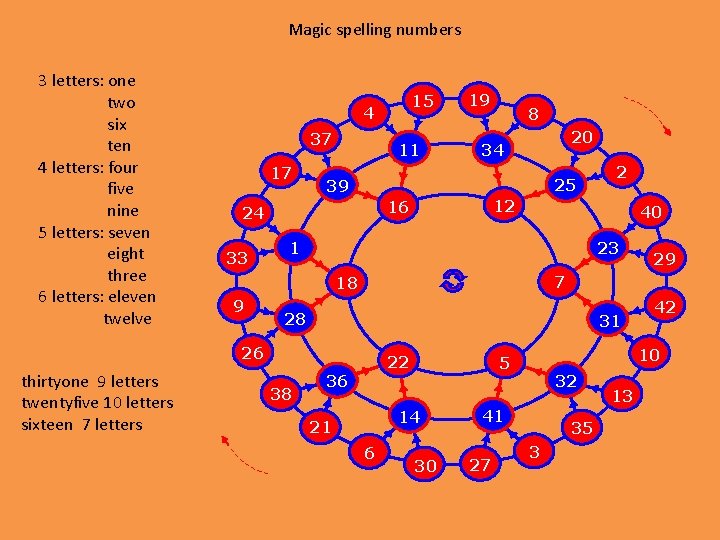
Magic spelling numbers 3 letters: one two six ten 4 letters: four five nine 5 letters: seven eight three 6 letters: eleven twelve 37 17 11 8 20 34 25 40 23 1 28 38 29 7 18 9 2 12 16 24 33 19 39 31 26 thirtyone 9 letters twentyfive 10 letters sixteen 7 letters 15 4 22 36 6 10 5 14 21 30 32 41 27 42 35 3 13
Guess the number We secretly select a number from 1 to 20. We place on the above card those of the cards on the next page that contain our number


Suppose, you have chosen the number 7

Think of a number from 1 to 31 and find out which of the following cards contain it. I can guess your number
- Slides: 30