Mathematical Logic Data and Knowledge Representation Originally by

Mathematical Logic Data and Knowledge Representation Originally by Alessandro Agostini and Fausto Giunchiglia Modified by Fausto Giunchiglia, Rui Zhang and Vincenzo Maltese

Outline q Modeling q q and logical modeling Domain Language Theory Model q Languages q Logic: formal languages q Using Logic q q q 2 Specification Automation Expressiveness Efficiency VS. Complexity Decidability
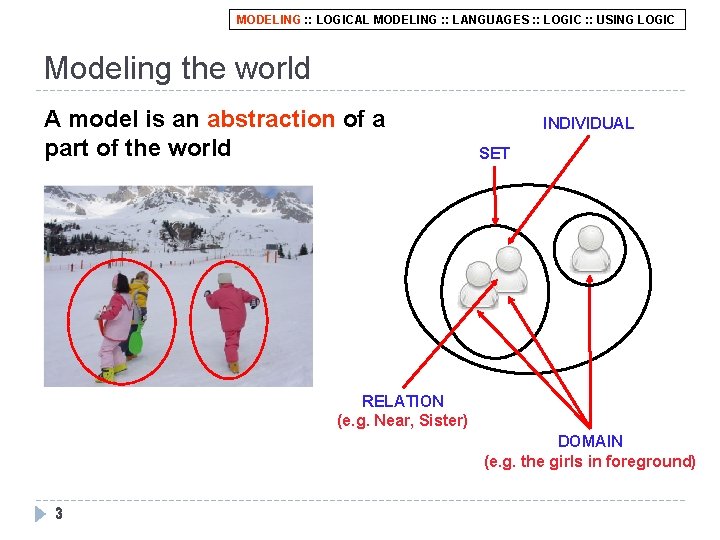
MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Modeling the world A model is an abstraction of a part of the world INDIVIDUAL SET RELATION (e. g. Near, Sister) DOMAIN (e. g. the girls in foreground) 3
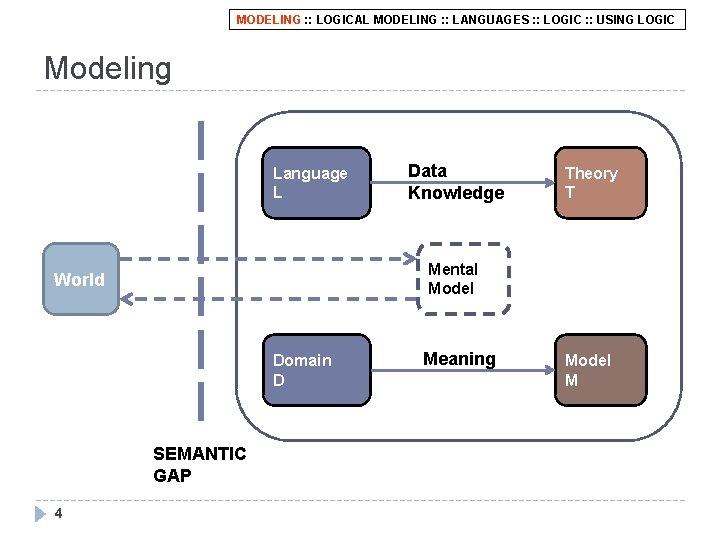
MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Modeling Language L Theory T Mental Model World Domain D SEMANTIC GAP 4 Data Knowledge Meaning Model M

MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Modeling: explained World: the phenomenon we want to describe q Domain: the abstract relevant elements in the real world q Mental Model: what we have in mind. It is the first abstraction of the world (subject to the semantic gap) q Language: the set of words and rules we use to build sentences used to express our mental model q Theory: the set of sentences (constraints) about the world expressed in the language that limit the possible models q Model: the formalization of the mental model, i. e. the set of true facts in the language, in agreement with theory q Semantic gap: the impossibility to capture the entire reality q NOTE: this does not necessarily need to be in formal semantics 5

MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Mental models There is a monkey in a laboratory with some bananas hanging out of reach from the ceiling. A box is available that will enable the monkey to reach the bananas if he climbs on it. The monkey and box have height Low, … … but if the monkey climbs onto the box he will have height High, the same as the bananas. [. . . ]” NOTE: each picture is a different model 6
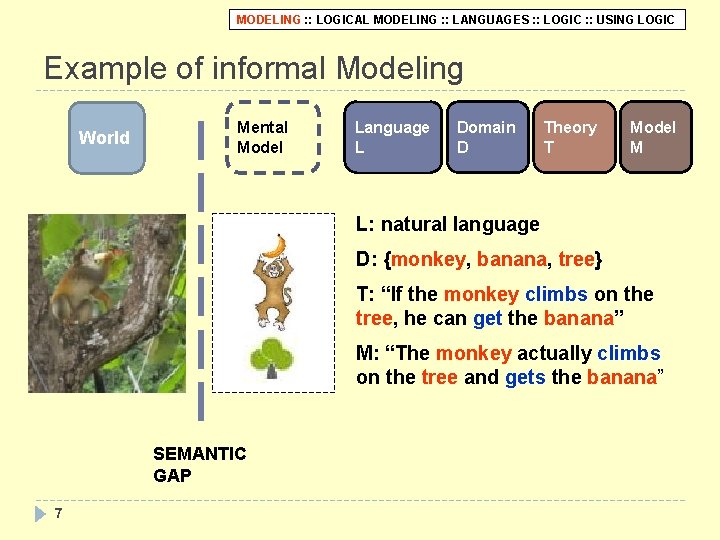
MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Example of informal Modeling World Mental Model Language L Domain D Theory T Model M L: natural language D: {monkey, banana, tree} T: “If the monkey climbs on the tree, he can get the banana” M: “The monkey actually climbs on the tree and gets the banana” SEMANTIC GAP 7
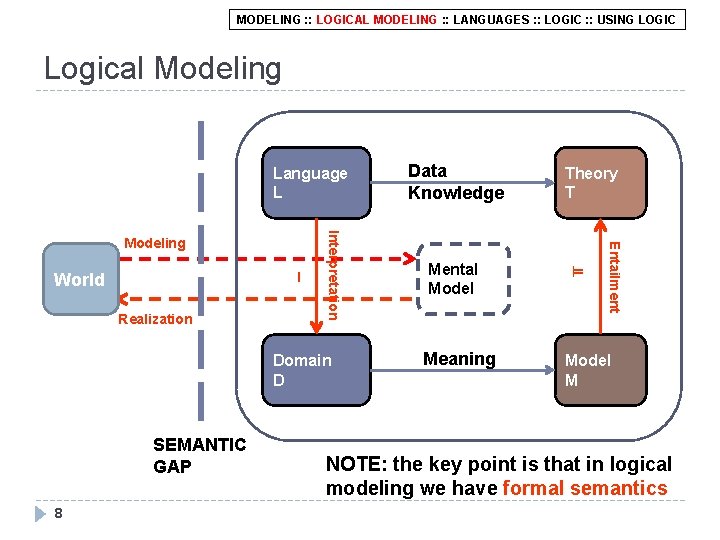
MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Logical Modeling Language L Realization Domain D SEMANTIC GAP 8 Mental Model Meaning Theory T ⊨ Entailment I World Interpretation Modeling Data Knowledge Model M NOTE: the key point is that in logical modeling we have formal semantics

MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Logical Modeling: explained Domain: relevant objects q Logical Language: the set of formal words and rules we use to build complex sentences q Interpretation: the function that associates elements of the language to the elements in the domain q Theory / Knowledge Base (KB): the set of facts which are always true (in data and knowledge) q Model: the set of true facts in the language describing the mental model (the part of the world observed), in agreement with theory q Truth-relation / logical entailment (⊨): deduction, reasoning, inference q 9

MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Intensional vs Extensional semantics q Intensional: I can only express the fact that a given proposition is true or false “Bananas are yellow” “All men are mortal” Girls. Playing = True q “Bananas have a curve shape” man mortal Extensional: I provides the objects of the domain corresponding to the proposition “The author of Romeo and Juliet is Shakespeare” author(R&G, Shakespeare) Girls. Playing = {Mary, Sara, Julie} 10
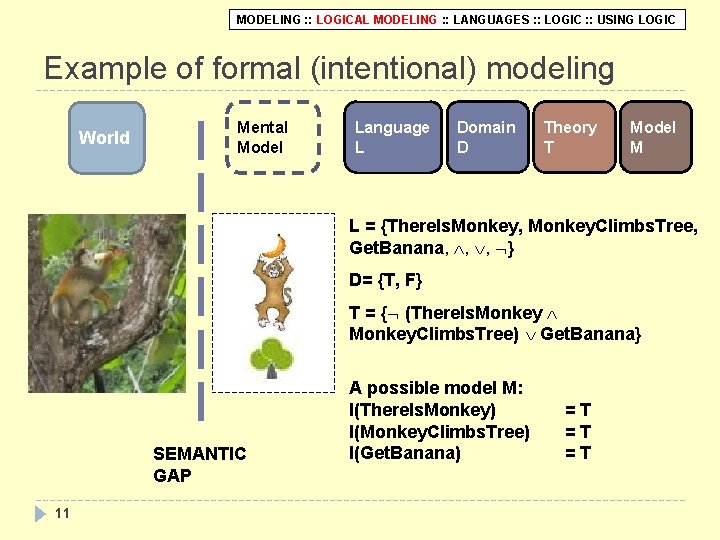
MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Example of formal (intentional) modeling World Mental Model Language L Domain D Theory T Model M L = {There. Is. Monkey, Monkey. Climbs. Tree, Get. Banana, , , } D= {T, F} T = { (There. Is. Monkey. Climbs. Tree) Get. Banana} SEMANTIC GAP 11 A possible model M: I(There. Is. Monkey) I(Monkey. Climbs. Tree) I(Get. Banana) =T =T =T
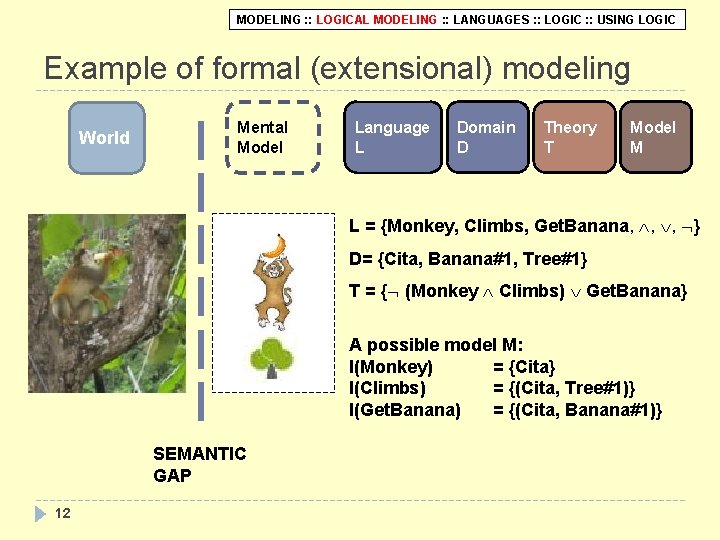
MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Example of formal (extensional) modeling World Mental Model Language L Domain D Theory T Model M L = {Monkey, Climbs, Get. Banana, , , } D= {Cita, Banana#1, Tree#1} T = { (Monkey Climbs) Get. Banana} A possible model M: I(Monkey) = {Cita} I(Climbs) = {(Cita, Tree#1)} I(Get. Banana) = {(Cita, Banana#1)} SEMANTIC GAP 12

MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Language q. A (usually finite) set of words (the alphabet) and rules to compose them to build “correct sentences” e. g. Monkey and Get. Banana are words q e. g. Monkey Get. Banana is a sentence (rule: A B) q q. A tool for codifying our (mental) model (what we have in mind): Sentences (syntax) with an intended meaning (semantics) q e. g. with the word Monkey we mean q 13

MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Language and correctness q We need an algorithm for checking correctness of the sentences in a language s, L q We Yes, correct! PARSER No say that a language is decidable if it is possible to create such a tool that in finite time can take the decision 14

MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Syntax and Semantics q Syntax: the way a language is written: q q q Syntax is determined by a set of rules saying how to construct the expressions of the language from the set of atomic tokens (i. e. , terms, characters, symbols). The set of atomic tokens is called alphabet of symbols, or simply the alphabet). Semantics: the way a language is interpreted: q q 15 It determines the meaning of the syntactic constructs (expressions), that is, the relationship between syntactic constructs and the elements of some universe of meanings (the intended model). Such relationship is called interpretation.

MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Example of Syntax and Semantics q Suppose we want to represent the fact that Mary and Sara are near each other. ENGLISH Mary is near Sara. formal syntax, informal semantics ‘SYMBOLIZED’ ENGLISH near(M, S) near(Mary, Sara) formal syntax, informal semantics LOGICS with an interpretation function I “near” by I it means near as spatial relation “M” by I it means Mary the girl “S” by I it means Sara the girl formal syntax, formal semantics 16

MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Formal vs. Informal languages q Language = Syntax q Formal syntax (what we write) + Semantics (what we mean) Infinite/finite (always recognizable) alphabet q Finite set of formal constructors and building rules for phrase construction q Algorithm for correctness checking (a phrase in a language) q q Formal q Semantics The relationship between syntactic constructs in a language L and the elements of an universe of meanings D is a (mathematical) function I: L pow(D) q Informal q 17 syntax/semantics the opposite of formal, namely the absence of the elements above.
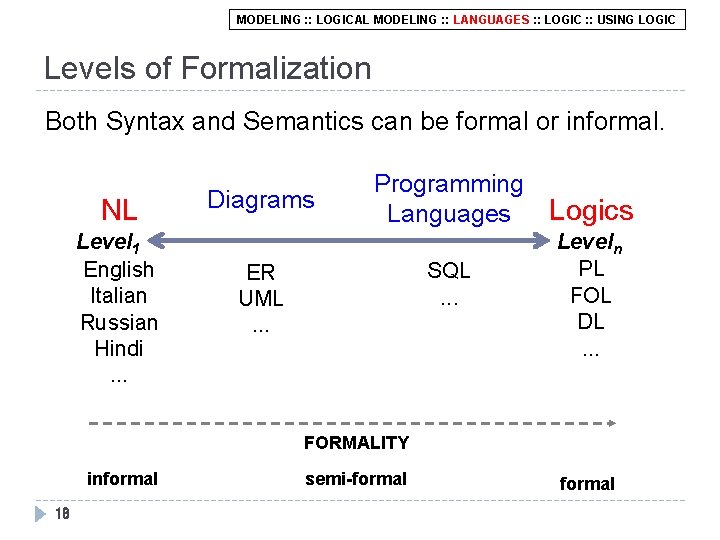
MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Levels of Formalization Both Syntax and Semantics can be formal or informal. NL Level 1 English Italian Russian Hindi. . . Diagrams Programming Languages SQL. . . ER UML. . . Logics Leveln PL FOL DL. . . FORMALITY informal 18 semi-formal
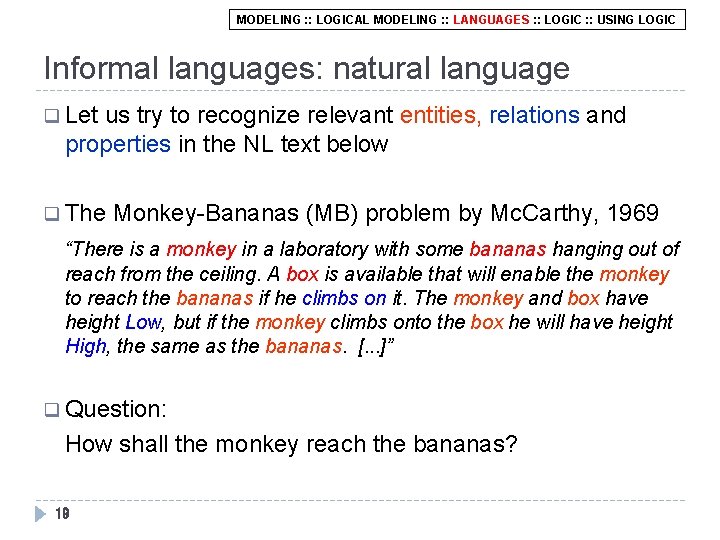
MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Informal languages: natural language q Let us try to recognize relevant entities, relations and properties in the NL text below q The Monkey-Bananas (MB) problem by Mc. Carthy, 1969 “There is a monkey in a laboratory with some bananas hanging out of reach from the ceiling. A box is available that will enable the monkey to reach the bananas if he climbs on it. The monkey and box have height Low, but if the monkey climbs onto the box he will have height High, the same as the bananas. [. . . ]” q Question: How shall the monkey reach the bananas? 19
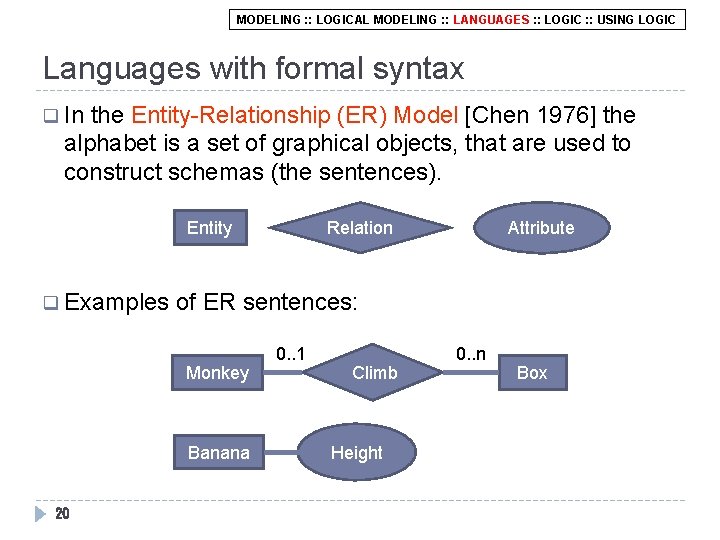
MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Languages with formal syntax q In the Entity-Relationship (ER) Model [Chen 1976] the alphabet is a set of graphical objects, that are used to construct schemas (the sentences). Entity q Examples Attribute of ER sentences: Monkey Banana 20 Relation 0. . 1 Climb Height 0. . n Box

MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Languages with formal syntax and semantics q Logics has two fundamental components: q L is a formal language (in syntax and semantics) q I is an interpretation function which maps sentences into a formal model M (over all possible ones) with a domain D Domain D = {T, F} or D’ = {o 1, …, on} q Language L = {A, , , } q Interpretation I: L D is intensional or I: L pow(D’) is extensional q Theory: a set of sentences which are always true in the language (facts) q Model: the set of true facts in the language describing the mental model (the part of the world observed), in agreement with theory q 21

MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Theory A theory T is set of facts: q A fact written in the language L defines a piece of knowledge (something true) about the domain D q A theory can be seen as a set of constraints on possible models to filter out all undesired ones 22

MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Data and Knowledge is factual information about what is true in general (axioms and theorems) e. g. singers sing songs q Data is factual information about specific individuals (observed knowledge) e. g. Michael Jackson is a singer q A finite theory T is called: q An ontology if it contains knowledge only q A knowledge base (KB) if it contains knowledge and data q A database (DB) if it only contains data. q A database + its schema is the simplest kind of knowledge base NOTE: Sometimes the terms Ontology and KB are used interchangeably 23

MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Model A model M is an abstract (in mathematical sense) representation of the intended truths via interpretation I of the language L e. g. Madonna is a singer, Sting is a singer, … M ⊨ T (M entails T) iff M ⊨ A, for each formula A in T A model M of a theory T is any interpretation function that satisfies all the facts in T (M satisfies T) q There can be many models satisfying theory T. They are a subset of all possible interpretation functions over L. q In case there are no models for T, we say that theory T is unsatisfiable. q 24

MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Usages of Representation Languages The two purposes in modeling q Specification: q Representation of the problem at the proper level of abstraction q Allow informal/formal syntax and informal/formal semantics q Automation (Automated Reasoning) q Computing consequences or properties of the chosen specifications q It requires formal semantics. q Logics 25 have formal syntax and formal semantics!
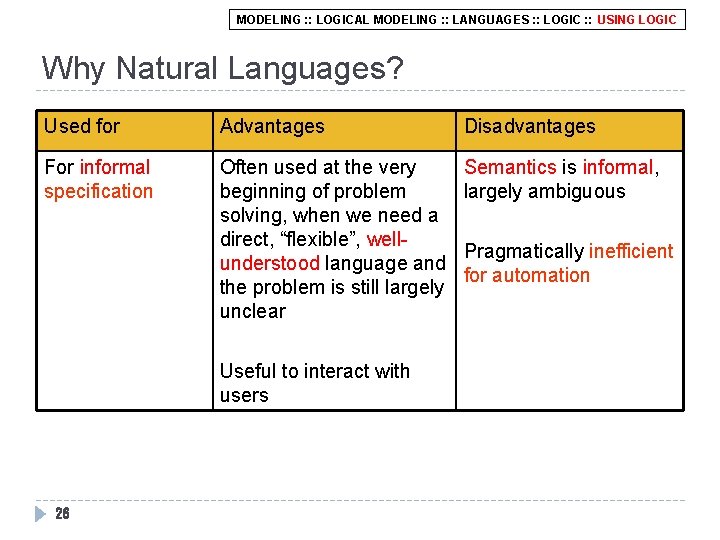
MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Why Natural Languages? Used for Advantages Disadvantages For informal specification Often used at the very beginning of problem solving, when we need a direct, “flexible”, wellunderstood language and the problem is still largely unclear Semantics is informal, largely ambiguous Useful to interact with users 26 Pragmatically inefficient for automation
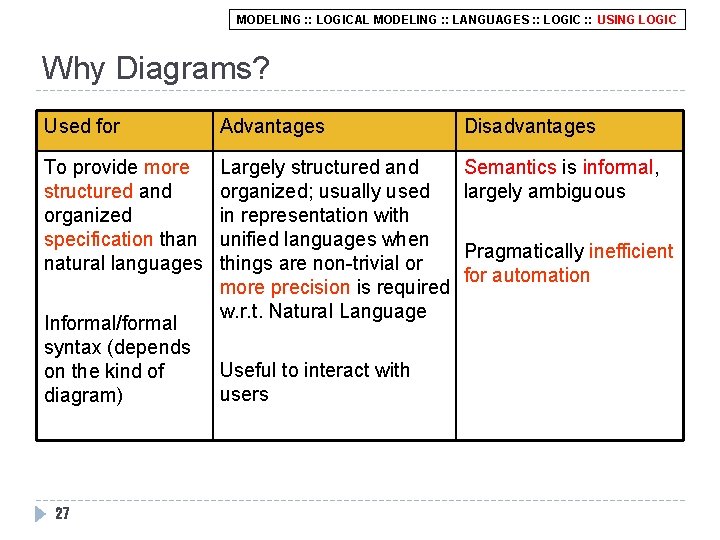
MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Why Diagrams? Used for Advantages Disadvantages To provide more structured and organized specification than natural languages Largely structured and organized; usually used in representation with unified languages when things are non-trivial or more precision is required w. r. t. Natural Language Semantics is informal, largely ambiguous Informal/formal syntax (depends on the kind of diagram) 27 Useful to interact with users Pragmatically inefficient for automation
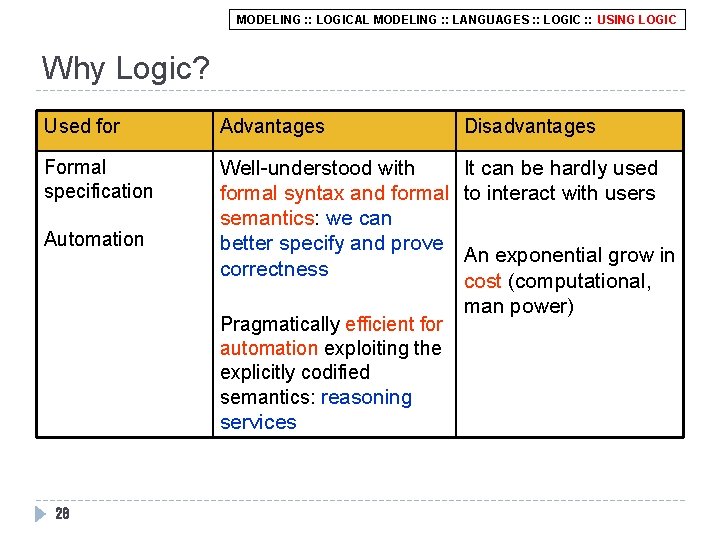
MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Why Logic? Used for Advantages Formal specification Well-understood with It can be hardly used formal syntax and formal to interact with users semantics: we can better specify and prove An exponential grow in correctness cost (computational, man power) Pragmatically efficient for automation exploiting the explicitly codified semantics: reasoning services Automation 28 Disadvantages

MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Logics for Automation: reasoning Logics provides a notion of deduction q axioms, deductive machinery, theorem q Deduction can be used to implement reasoners q Reasoners allow inferring conclusions from known facts (i. e. , a set of “premises”, premises can be axioms or theorems). q From implicit knowledge to explicit knowledge q q Reasoning services: q Model Checking (EVAL) Is a sentence ψ true in model M? q Satisfiability (SAT) Is there a model M where ψ is true? q Validity (VAL) Is ψ true according to all possible models? q Entailment (ENT) ψ1 true implies ψ2 true (in all models) 29

MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC How to use logical modeling in practice 1. Define a logic q q 2. Choose the right logic for the problem q 3. Given a problem the computer scientist must choose the right logic, most often one of the many available Write theory q 4. most often by reseachers once for all (not a trivial task!) The computer scientist writes a theory T Use reasoning services q 30 Computer scientists use reasoning services to solve their programs

MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC An Important Trade-Off q There is a trade-off between: expressive power (expressiveness) and q computational efficiency provided by a (logical) language q q This trade-off is a measure of the tension between specification and automation q To use logic for modeling, the modeler must find the right trade off between expressiveness in the language for more tractable forms of reasoning services. 31
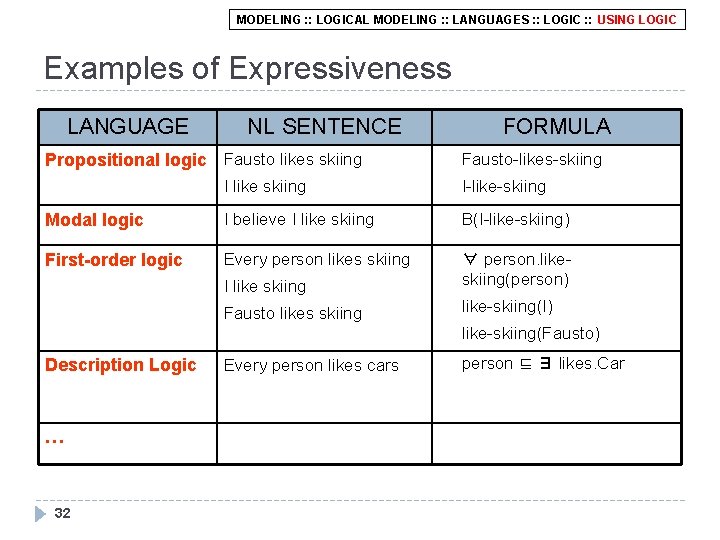
MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Examples of Expressiveness LANGUAGE NL SENTENCE Propositional logic Fausto likes skiing FORMULA Fausto-likes-skiing I like skiing I-like-skiing Modal logic I believe I like skiing B(I-like-skiing) First-order logic Every person likes skiing I like skiing ∀ person. likeskiing(person) Fausto likes skiing like-skiing(I) like-skiing(Fausto) Description Logic … 32 Every person likes cars person ⊑ ∃ likes. Car

MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Efficiency VS. Complexity q Efficiency q q Performing in the best possible manner; satisfactory and economical to use [Webster] In modeling it applies to reasoning In time, space, consumption of resources Complexity (or computational complexity) of reasoning q q The difficulty to compute a reasoning task expressed by using a logic With degrees of expressiveness, we may classify the logical languages according to some “degrees of complexity” NOTE: When logic is used we always pay a performance price and therefore we use it when it is cost-effective 33

MODELING : : LOGICAL MODELING : : LANGUAGES : : LOGIC : : USING LOGIC Decidability q The existence of an effective method to determine the validity of formulas in a logical language q. A logic is decidable if there is an effective method to determine whether arbitrary formulas are included in a theory q. A decision procedure is an algorithm that, given a decision problem, terminates with the correct yes/no answer. q In this course we focus on logics that are expressive enough to model real problems but are still decidable 34
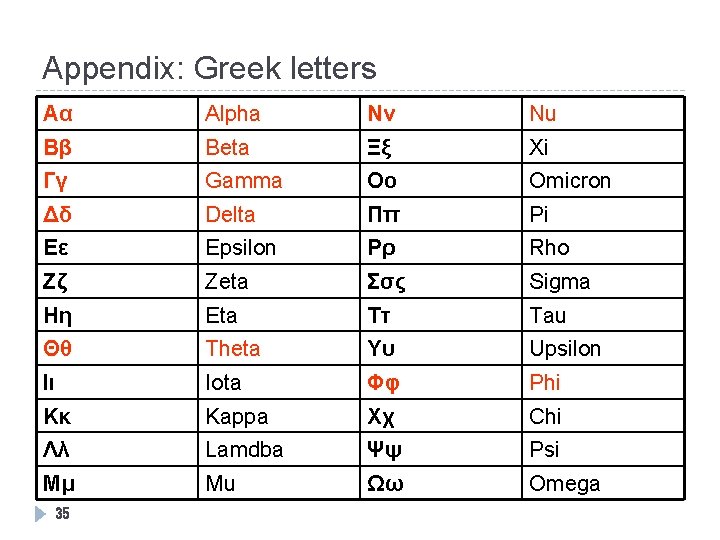
Appendix: Greek letters Αα Alpha Νν Nu Ββ Beta Ξξ Xi Γγ Gamma Οο Omicron Δδ Delta Ππ Pi Εε Epsilon Ρρ Rho Ζζ Zeta Σσς Sigma Ηη Eta Ττ Tau Θθ Theta Υυ Upsilon Ιι Iota Φφ Phi Κκ Kappa Χχ Chi Λλ Lamdba Ψψ Psi Μμ Mu Ωω Omega 35
- Slides: 35