MATHEMATICAL LITERACY GRADE 10 CAPS TOPIC 5 Maps

MATHEMATICAL LITERACY GRADE 10 CAPS TOPIC 5: Maps, plans and other representations of the physical world Section 5. 1: Scale

Topic 5: Maps, plans and other representations of the physical world The following sections will be covered: 5. 1. Scale 5. 2. Maps 5. 3. Plans (instruction/assemble diagrams) 5. 4. Plans (floor, elevation and design plans)

Scale In Section 5. 1, learners will be able to: § Work with Number Scales and Bar Scales. § Calculate actual length and distance when map/plan measurement are known. § Understand the advantages and disadvantages of Number Scale and Bar Scale.

§ Scale is a ratio between two units of measure. § The two units of measure are the distance measured on map and the actual distance on the ground. § Scale is used to calculate actual distances. § The two types of scale: Number scale and Bar Scale.

Number Scale �Number scale is expressed in the form 1 : n, where n stands for a number eg 1 : 50 000 meaning 1 unit on the map is equivalent 50 000 units on the ground. so 1 cm = 50 000 cm 1 cm = 500 m 1 cm = 0, 5 km

Number Scale cont. Advantages of Number Scale: �No units are included. �The relationship between the length on the plan and the actual length is the same. Disadvantages of The Number Scale: �When maps or plans are reduced or enlarged, the number scale becomes invalid. �The correct scale can only be found if the numbers are multiplied or divided by the same factor used to reduce/enlarge the map.

Activity 1: a) A map of South Africa has a scale of 1 : 50 000. (i) Write this scale as 1 cm on the map = _____cm on the map. (ii) Write this scale as 1 cm on the map = _____km on the ground. ________________________ b) Simplify the following scale 3 cm : 3 m

Solution: Activity 1 a) (i) 50 000 cm (ii) 50 km

Solution: Activity 1 b) 3 cm : 3 m 1 cm : 1 m 1 : 100 Step 1: Divide both sides by 3 Step 2: Change 1 m to cm

Bar Scale A Bar Scale is of the form:

Bar Scale cont. On previous slide the scale: 50 mm = 1 m or 5 cm = 1 m or 0, 05 m = 1 m

Bar Scale cont. Advantages: �It is easy to use. �If a map is enlarged or reduced, the bar scale on the map will change in size proportionally. � Any unit of measure can be shown or indicated. Disadvantages: �The ratios have different units which have to be changed to the same units.

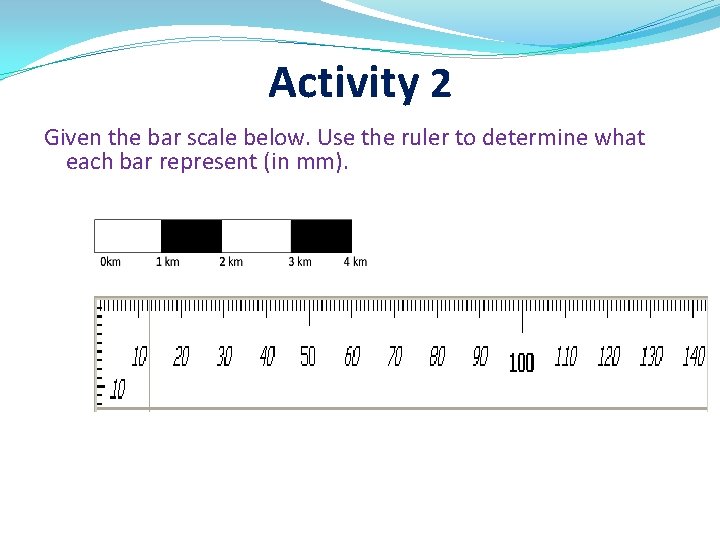
Activity 2 Given the bar scale below. Use the ruler to determine what each bar represent (in mm). 1 km 2 km 3 km

Solutions: Activity 2 18 mm represent 1 km 30 mm represent 2 km. 48 mm represent 3 km. 60 mm represent 4 km.

Calculations with Number Scales Determining actual real-world length or distance when a measurement on the plan is known;

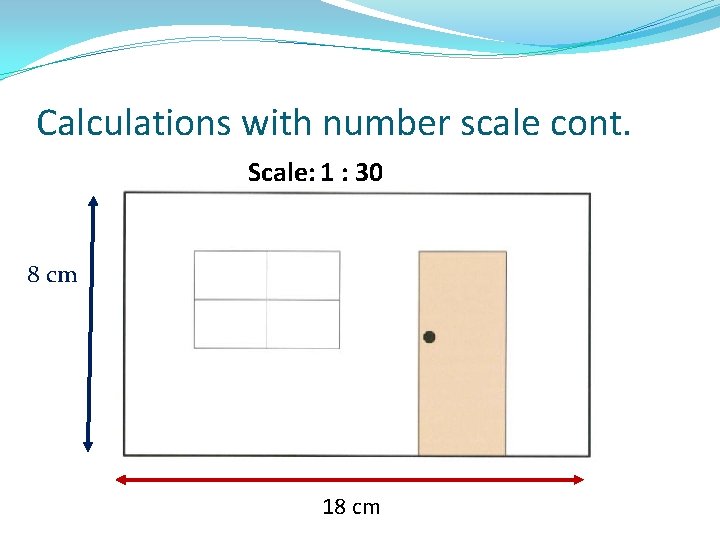
Calculations with number scale cont. Scale: 1 : 30 8 cm 18 cm

Calculations with Number Scale cont. �If the scale is 1 : 30 this means that: �the actual measurements are 30 times bigger than the measurements on the picture. So: Length on plan = 18 cm → Actual length = 18 cm × 30 = 540 cm Height on plan = 8 cm → Actual height = 8 cm × 30 = 240 cm

Calculations with Bar Scale Example: A floor plan of a room is given below.

Calculations with Bar Scale cont.

Calculations with Bar Scale cont. Measure the bar scale to determine the relationship between a measure on a ruler and actual distance. On the floor plan of the office: Bar Scale: 2 cm = 3 m Rewrite to bar scale to work out the number of metres equal to 1 cm (or 1 mm): Bar Scale: 2 cm = 3 m 1 cm = 1, 5 m

Calculations on Bar Scale cont. Measure the required length on the plan and then use the bar scale written in the form 1 cm = … m to determine actual length. Length of room 1 on plan = 3, 6 cm Bar Scale: 1 cm = 1, 5 m Actual length = 3, 6 cm × 1, 5 m/cm � = 5, 25 m

Final Assessment Questions 1 -10 Question 1 A map of South Africa has a scale of 1 : 5 000. Write this scale as: 1 cm 0 n the map = ____cm on the ground. A. 5 000 B. 5 00 000 C. 5 000 D. 5

Question 2 A map of South Africa has a scale of 1 : 5 000. Write this scale as: 1 cm on the map = ____km on the ground. A. 5 000 B. 50 C. 500 000 D. 5 000

Question 3 Simplify the scale 50 cm : 1 200 km to a scale that will be easy to work with A. 1 : 120 B. 1 : 240 C. 1 : 2 400 D. 1 : 2 400 000

Question 4 Which of the scales below indicate the small scale map: A. 1 : 1 000 B. 1 : 625 000 C. 1 : 50 000 D. 1 : 10 000

Question 5 The straight line distance between Cape Town and Johannesburg on the map is 80 mm. Use the scale 1: 16 000 to determine this distance in kilometres. A. B. C. D. 16 000 km 1600 km 12 800 km 1280 km

Question 6 Johan measured the distance between Town and Newcastle Hospital as 518 cm. How far is this distance on the ground using the scale 1 : 1 000. A. 5 180 cm B. 5 1800 cm C. 518 000 cm D. 518 cm

Question 7 An architect is drawing a plan of a house in the scale of 1 : 20. If the actual height of the house is 4, 5 m, the height on the plan in cm will be: A. B. C. D. 22, 5 cm 22 cm 2, 25 cm 2. 3 cm

Question 8 When maps or plans are reduced or enlarged, the _____ scale become invalid. A. Enlarged Scale B. Bar Scale C. Number Scale D. Reduced Scale

Question 9 The Bar Scale of 3 m measure 2 cm on the plan. If the length of the window on plan is 3, 5 cm, then the actual length on ground will be: 1. 5, 25 cm 2. 5, 25 m 3. 21 m 4. 21 cm

Question 10 If the actual length measure 5, 5 m and the measure on plan is 11 cm then the scale will be: A. 1 : 500 B. 1 : 50 C. 1 : 550 D. 1 : 5 000

Solutions: Final Assessment Questions 1. C 2. 2 3. D 4. A 5. D 6. C 7. A 8. C 9. B 10. B