Mathematical Knowledge for Teaching at the Secondary Level

Mathematical Knowledge for Teaching at the Secondary Level: Experts Conference University Park, PA May 20 -22, 2007 Mid Atlantic Center for Mathematics Teaching and Learning Center for Proficiency in Teaching Mathematics

Situations Research Group Glen Blume M. Kathleen Heid Jeremy Kilpatrick Jim Wilson Pat Wilson Rose Mary Zbiek Bob Allen Sarah Donaldson Kelly Edenfield Ryan Fox Heather Godine Shiv Karunakaran Evan Mc. Clintock

Expert Advisors Tom Banchoff, Brown University Steve Benson, EDC Al Cuoco, EDC Helen Doerr, Syracuse University Jim Fey, University of Maryland Karen Graham, University of New Hampshire Neil Portnoy, University of New Hampshire Sharon Senk, Michigan State University Ed Silver, University of Michigan Glenn Stevens, Boston University Zal Usiskin, University of Chicago

Welcome David Monk, Dean, College of Education Murry Nelson, Chair, Dept. of Curriculum and Instruction

Mathematical Knowledge for Teaching Mathematics at the Secondary Level

What is Mathematical Knowledge for Teaching Mathematics at the Secondary Level Why is MKT difficult to define? What is the difference between MKT and Mathematical knowledge? Pedagogical content knowledge? Is MKTS distinct from MK or from MKT at the elementary level?

Recommendations on Formal Mathematics Course Background for Secondary Teachers 1911 ICTM: “dealing critically with the field of elementary mathematics from the higher standpoint” 1935 MAA: “calculus, Euclidean geometry, theory of equations, and a history of mathematics course” 1959 NCTM: 24 semester hours of mathematics courses

Recommendations on Formal Mathematics Course Background for Secondary Teachers 1991 MAA’s Committee on the Mathematical Education of Teachers (COMET): “the equivalent of a major in mathematics, but one quite different from that currently in place at most institutions” 2000 NCATE: “know the content of their field (a major or the substantial equivalent of a major)” Compiled in Ferrini-Mundy and Findell

MET Report Recommendations Knowledge of the mathematical understandings and skills of elementary and middle school students Knowledge of the post-secondary mathematics (collegiate, vocational or work). Ability to continue growth of mathematical knowledge and its teaching.

MET Report Recommendations R Understanding of the properties of the natural, integer, rational, real, and complex number systems. R Understanding of the ways that basic ideas of number theory and algebraic structures underlie rules for operations on expressions, equations, and inequalities. R Understanding and skill in using algebra to model and reason about real-world situations. R Ability to use algebraic reasoning effectively for problem solving and proof in number theory, geometry, discrete mathematics, and statistics. R Understanding of ways to use graphing calculators, computer algebra systems, and spreadsheets to explore algebraic ideas and algebraic representations of information, and in solving problems.

Secondary mathematics teachers should understand ways to think about mathematical understanding Concept images/concept definitions (Tall & Vinner) Process/object understanding (Dubinsky; Sfard) Interviewing students (Heid, Blume, Zbiek, Edwards)

Research on Formal Mathematics Course Background of Secondary Teachers and Student Achievement Monk, D. (1994). Subject area preparation of secondary mathematics and science teachers and student achievement. Economics of Education Review, 13(2) 125 -145.

Results from Monk study: Effects of more mathematics courses Effects of more mathematics education courses Differential effect of more math courses or more math education courses? Degree level, math major, teaching experience

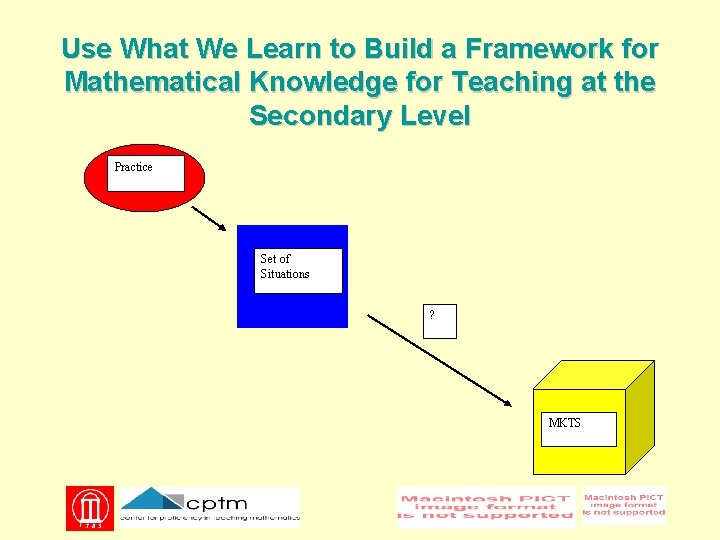
Strategy for Learning about Mathematical Knowledge for Teaching at the Secondary Level Begin with practice Identify mathematical ideas and ways of thinking about mathematics that could be useful to secondary mathematics teachers Use what we learn to build a way to think about Mathematical Knowledge for Teaching at the Secondary level

Begin with Practice We draw from events that have been witnessed in practice. – Practice includes but is not limited to classroom work with students. – Events were in high schools or universities. – Events were related to secondary level mathematics. We write brief prompts that describe mathematical events from practice.

Identify Mathematical Ideas and Ways of Thinking about Mathematics Given an event from practice (Prompt), – We describe the mathematical ideas that could be useful to a teacher in that situation – We are not trying to decide what a teacher should do! We write a Situation which includes the practice-based Prompt and a set of Foci and Commentary.

Then we… Argue and rewrite Debate and rewrite Defend and rewrite Rethink and rewrite. . .

Use What We Learn to Build a Framework for Mathematical Knowledge for Teaching at the Secondary Level Practice Set of Situations ? MKTS

Looking at Situations in small groups How does your assigned situation contribute to or support your understanding of Mathematical Knowledge for Teaching at the Secondary level?

Small Group Work Grouping is by Situation 3: Rm 116 Situation 40: Rm 104 Situation 41: Rm 104 Situation 46: Rm 104 Return by 9: 30

A Set of Situations If we had a good set of Situations what are the characteristics of that set that would help us conceptualize Mathematical Knowledge for Teaching at the Secondary level?

Situations We are in the process of writing a set of practice-based situations that will help us to identify mathematical knowledge for teaching at the secondary level. Each Situation consists of: • Prompt - generated from practice • Commentaries - providing rationale and extension • Mathematical Foci - created from a mathematical perspective

Prompts A prompt describes an opportunity for teaching mathematics E. g. , a student’s question, an error, an extension of an idea, the intersection of two ideas, or an ambiguous idea. A teacher who is proficient can recognize this opportunity and build upon it.

Commentaries The first commentary offers a rationale for each focus and emphasizes the importance of the mathematics that is addressed in the foci. The second commentary offers mathematical extensions and deals with connections across foci and with other topics.

Mathematical Foci The mathematical knowledge that teachers could productively use at critical mathematical junctures in their teaching. Foci describe the mathematical knowledge that might inform a teacher’s actions, but they do not describe or suggest specific pedagogical actions.

Mathematical Lenses Mathematical Objects Big Mathematical Ideas Mathematical Activities of Teachers

Mathematical Lens: Mathematical Objects A “mathematical-objects” approach • Centers on mathematical objects, properties of those objects, representations of those objects, operations on those objects, and relationships among objects; • Starts with school curriculum; and • Addresses the larger mathematical structure of school mathematics.

Mathematical Lens: Big Mathematical Ideas A “big-mathematical-ideas” approach • Centers on big ideas or overarching themes in secondary school mathematics; • Examples: ideas about equivalence, variable, linearity, unit of measure, randomness; • Begins with a mix of curriculum content and practice and uses each to inform the other; and • Accounts for overarching mathematical ideas that cut across curricular boundaries and carry into collegiate mathematics while staying connected to practice.

Mathematical Lens: Mathematical Activities of Teachers A “mathematical-activities” approach • Partitions or structures the range of mathematical activities in which teachers engage • Examples: defining a mathematical object, giving a concrete example of an abstraction, formulating a problem, introducing an analogy, or explaining or justifying a procedure. • May also draw on the mathematical processes that cut across areas of school mathematics.

Looking at the Inverse Trig Function Mathematical Foci through an Object Lens Focus 1: Inverse Focus 2: Relationship between graphs of inverse functions Focus 3: A conventional symbolic representation of “the inverse of ” f is f -1. The exponent or superscript -1 has several different meanings, not all of which are related to inverse in the same way.

Looking at the Inverse Trig Function Mathematical Foci through an Big Ideas Lens Focus 1: Two elements of a set are inverses under a given binary operation defined on that set when the two elements used with the operation in either order yield the identity element of the set. Focus 2: Equivalent Functions/ Domain and Range: Two functions are equivalent only if they have the same domain and the same range. Focus 3: The same mathematical notation can represent related but different mathematical objects.

Looking at the Inverse Trig Function Mathematical Foci through an Activities Lens Focus 1: Appealing to definition to refute a claim Focus 2: Using a different representation to explain a relationship Focus 3: Explaining a convention