Mathematical Foundations of AI Lecture 10 Fair Allocation

Mathematical Foundations of AI Lecture 10 – Fair Allocation (Indivisible goods)

Content • Allocation of indivisible goods via deals • Social welfare • Envy freeness • Back to cake-cutting

Model • A finite set of items, that cannot be divided G = {g 1, g 2, …, gk} • A set of agents N = {1, 2, …, n} – Every agent has an evaluation function, which assigns a value for every subset of items Vi : 2 G R

Allocations • An allocation A is a partition of the set G, so that every agent gets several items (perhaps none) A = {A 1, …, An} , such that: – For all i≠j, Ai ∩ Aj is empty – All items in G are allocated

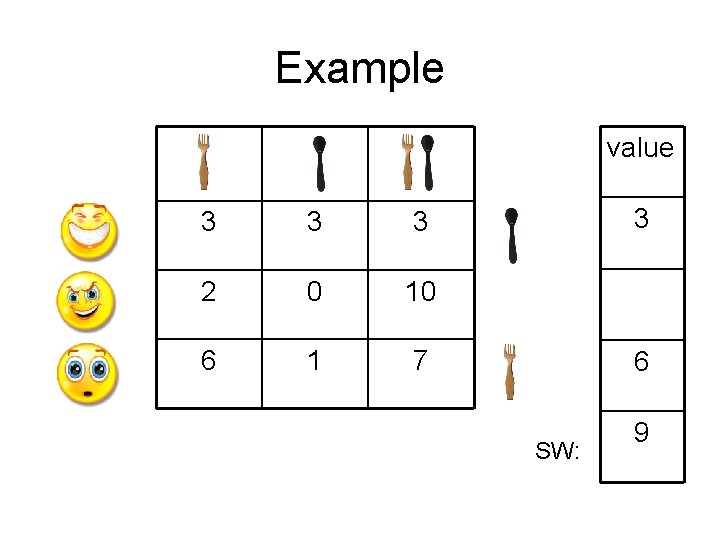
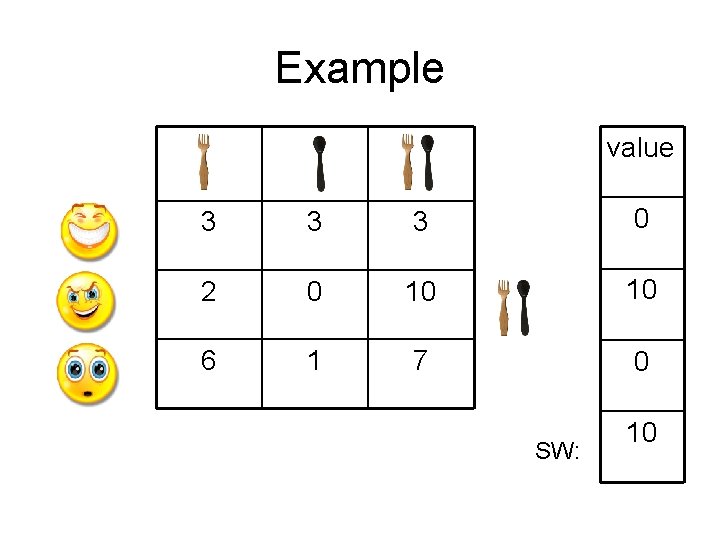
Social Welfare • We want an “objective” measure to the goodness of an allocation • We simply sum the utility of all agents: SW(A) = ΣVi(Ai) • Allocation A is called efficient, if it maximizes the social welfare – Note that efficiency does not imply fairness

Example value 3 3 3 2 0 10 6 1 7 3 6 SW: 9

Example value 3 3 3 0 2 0 10 10 6 1 7 0 SW: 10

Deals and Payments • One approach is an offline allocation of the goods by a central authority – Maximizing SW is NP-hard in the general case • We are interested is a situation where each agent makes its own decisions • To facilitate such decisions, we introduce “money” into the system

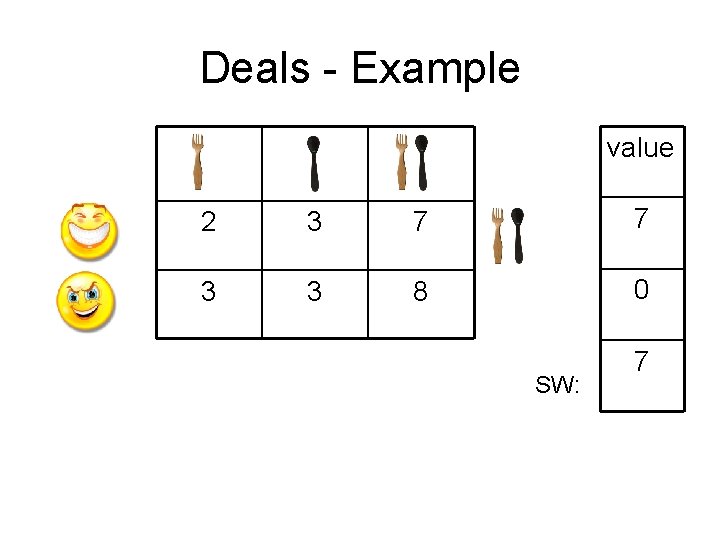
Deals and Payments (2) • A deal (A, A’) is transaction of items between agents so that the allocation changes from A to A’ • A payment vector P=(P 1, …Pn) determines how much each agent “pays” – The sum of payments is always 0.

Deals and Payments (3) • A deal (A, A’) is individually rational, if there is a payment vector P such that Vi(A’i)-Vi(Ai) ≥ Pi for every agent, and the inequality is strict for at least one agent. • This means each agent gains at least what he is paying.

Deals - Example value 2 3 7 7 3 3 8 0 SW: 7

Deals - Example value 2 3 7 2 3 3 8 3 Agent 1 has to “pay” at most 2 -7 = -5, i. e. to get at least 5 Agent 2 has to pay at most 3 -0 = 3 SW: 5

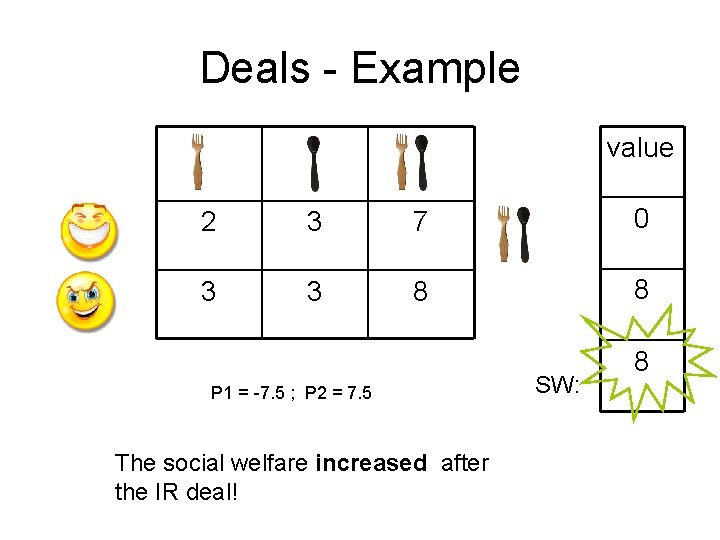
Deals - Example value 2 3 7 0 3 3 8 8 P 1 = -7. 5 ; P 2 = 7. 5 The social welfare increased after the IR deal! SW: 8

Rationality and Social Welfare Lemma 1: a deal (A, A’) is IR iff it strictly increases the social welfare Lemma 2: any sequence of IR deals is finite Theorem 3: any sequence of IR deals, from any initial allocation, will eventually reach an efficient allocation

Envy freeness • Without payments, envy-free allocations may not be possible – E. g. : we have only 1 item, wanted by 2 agents • We define a state as a pair S=(π, A) where π is a payment vector

Envy freeness (2) • A state S is envy-free, if no agent wants to switch places with another, i. e. if for all i, j Vi(Si)- πi ≥ Vi(Sj) – πj • Example: V 1 = 3 V 2 = 2 π1 = 1 π2 = -1 V 1 -π1 = 2 ≥ 1 =0 -π2 = 1 ≥ V 2 -π1

Envy freeness (2) • A state S is envy-free, if no agent wants to switch places with another, i. e. if for all i, j Vi(Si)- πi ≥ Vi(Sj) – πj • Example: V 1 = 3 V 2 = 2 π1 = -? -π1 ≥ 3 - π2 π2 = ? > 2 – π2 ≥ -π1

EEF • We want to reach a state that is both Efficient and Envy-free (EEF) • There is always an EEF – We will prove for a less general case

Super additivity • An evaluation function V is super additive, if for any distinct sets A, B V(A U B) ≥ V(A)+V(B) Theorem 4: if all agents have super additive evaluations, then there is an EEF state We take an efficient allocation A*, and add the payments πi = Vi(A*) – SW(A*)/n

Reaching EEF states • Consider the following initial state: V 1 = 3 V 2 = 2 V 1 – π1 = 0 V 2 - π2 = 2 V 1 – π1 ≤ 3 -2 =1 V 2 - π2 ≥ 2 • There is only IR deal, and it will make agent 1 pay at least 2, thus making it envy • But the state wasn’t fair in the first place!

Globally uniform payments • For every initial allocation A 0, we set the initial payment to π0 i = Vi(A 0) – SW(A 0)/n – The equitability condition • For every deal (A, A’), we define a globally uniform payment function (GUPF) Pi = Vi(A’)-Vi(A) – (SW(A’)-SW(A))/n These payments combine the private gain and the common gain. • An agent will pay more if the deal helps him • But less if this deal helps the society

Reaching EEF states (2) Theorem 5: If all Vi are super additive, and we start from any initial allocation A 0, with initial payments π0, then every sequence of IR deals with GUPF will reach an EEF state. • From Theorem 3 we know that efficiency is guaranteed, so we only need to prove envy freeness. • We simply show by induction that equitability still holds after each deal.

Approximate envy freeness • Suppose we cannot use payments for some reason – Legal – Practical – etc. • We may still want to “minimize” the envy that agents may feel towards others • Let eij(A) the “envyness” between i, j, in A • We want to minimize e(A) = max(eij(A))

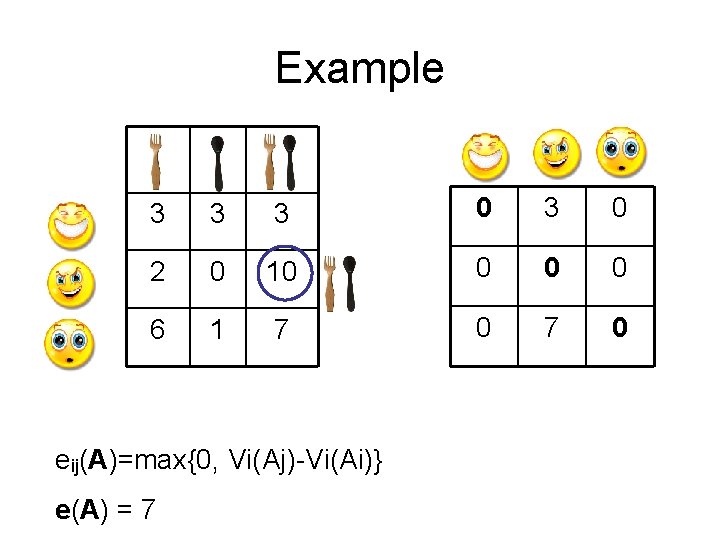
Example 3 3 3 0 2 0 10 0 6 1 7 0 eij(A)=max{0, Vi(Aj)-Vi(Ai)} e(A) = 7

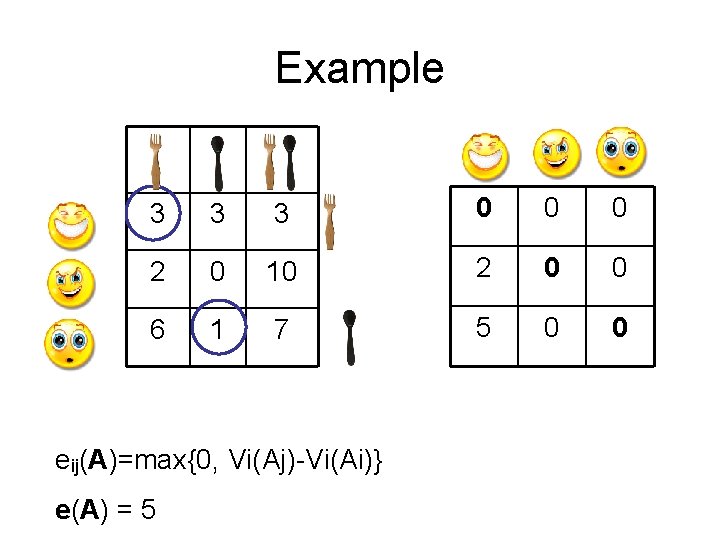
Example 3 3 3 0 0 0 2 0 10 2 0 0 6 1 7 5 0 0 eij(A)=max{0, Vi(Aj)-Vi(Ai)} e(A) = 5

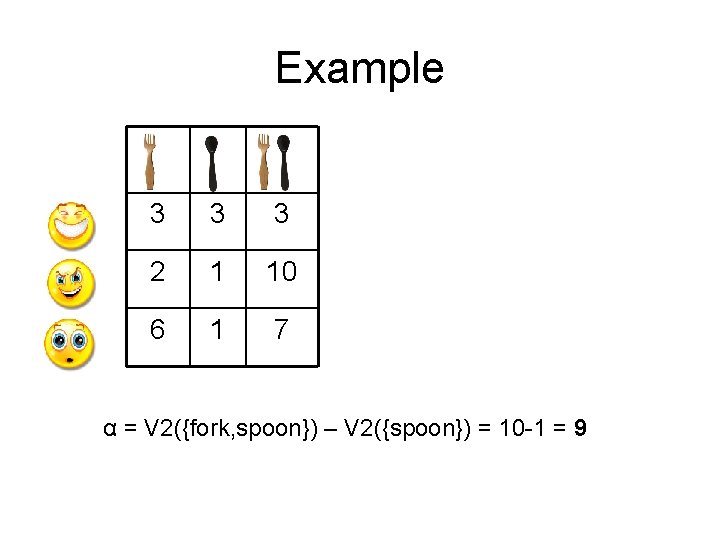
Marginal utility • The marginal utility of an item, is the value it adds to a set of items already owned – Depends on the agent and the set • The maximum marginal utility, is the maximal increase in utility of an agent, than can occur from getting one more item α = max [ Vi(G’ U {g}) – Vi(G’) ] The maximum is taken over all agents, all items g and all subsets of items G’

Example 3 3 3 2 1 10 6 1 7 α = V 2({fork, spoon}) – V 2({spoon}) = 10 -1 = 9

Bounding the envy Theorem 6: There is an allocation A, such that the total envy of A is bounded: e(A) ≤ α – Further, there is a polynomial algorithm that finds such an allocation

Back to cake cutting • We want a division whose total envy as at most ε • We can use the following protocol: – Each agent cuts the cake to pieces of size ≤ε – We now have O(n/ε) parts. The marginal value of each part is at most ε, thus α≤ε – We use the algorithm from theorem 6 to allocate the parts. We get that e(A)≤α≤ε Two types of queries are needed