Mathematical Formulas Ing Jaroslav Bernkopf Mathematical Formulas Objectives

Mathematical Formulas Ing. Jaroslav Bernkopf

Mathematical Formulas Objectives • Math symbols • Math operations • Expressing uncertainty http: //skola. bernkopf. cz jaroslav@bernkopf. cz 2

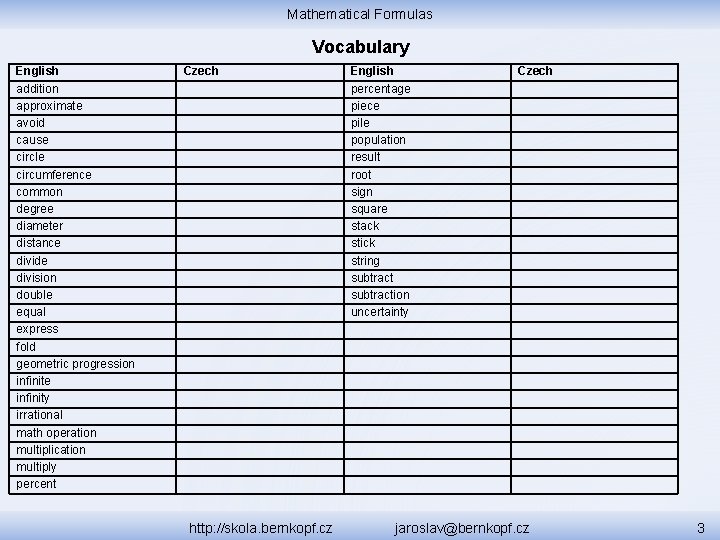
Mathematical Formulas Vocabulary English addition approximate avoid cause circle circumference common degree diameter distance divide division double equal express fold geometric progression infinite infinity irrational math operation multiplication multiply percent Czech http: //skola. bernkopf. cz English percentage piece pile population result root sign square stack stick string subtraction uncertainty Czech jaroslav@bernkopf. cz 3

Mathematical Formulas Math Symbols http: //www. youtube. com/watch? v=CG 0 Q 0 jo 2 v 6 k http: //skola. bernkopf. cz jaroslav@bernkopf. cz 4

Mathematical Formulas Math Symbols We will avoid numbers and stick to the language. The most basic symbols are + - x ÷ =. http: //skola. bernkopf. cz jaroslav@bernkopf. cz 5

Mathematical Formulas Math Symbols = The first of the common symbols is the equal sign. We say this as equals or is equal to. 1+1=2 http: //skola. bernkopf. cz jaroslav@bernkopf. cz 6

Mathematical Formulas Math Symbols + This is the addition sign. We say it as plus or add. 1+2, 4+9 http: //skola. bernkopf. cz jaroslav@bernkopf. cz 7

Mathematical Formulas Math Symbols The next one is the subtraction sign. We say it as minus, or subtract, or take. 1 -2, 13 -12, 99 -7 http: //skola. bernkopf. cz jaroslav@bernkopf. cz 8

Mathematical Formulas Math Symbols x, ∙ Then we have the multiplication sign. We say this as times or multiplied by. 3 x 8, 26∙ 3 http: //skola. bernkopf. cz jaroslav@bernkopf. cz 9

Mathematical Formulas Math Symbols ÷, / The next is the division sign. You can also show division as /. We say this as divided by, or over. 3 ÷ 1, 10 ÷ 5, 6 / 3 http: //skola. bernkopf. cz jaroslav@bernkopf. cz 10

Mathematical Formulas Math Symbols √ This one is the square root. We say the square root of. √ 4 = 2 http: //skola. bernkopf. cz jaroslav@bernkopf. cz 11

Mathematical Formulas Math Symbols % This one is the percentage sign. We say percent. 67% (per cent = out of 100) http: //skola. bernkopf. cz jaroslav@bernkopf. cz 12

Mathematical Formulas Math Symbols �� This one is Pi. This is a constant which begins 3. 141592653. . . This is an irrational number. c = �� xd The circumference of a circle equals �� times its diameter. http: //skola. bernkopf. cz jaroslav@bernkopf. cz 13

Mathematical Formulas Math Symbols ° The next symbol is the degree symbol. We say degrees. 90° 360° http: //skola. bernkopf. cz jaroslav@bernkopf. cz 14

Mathematical Formulas Math Symbols ∞ Then we have the symbol for infinity. http: //skola. bernkopf. cz jaroslav@bernkopf. cz 15

Mathematical Formulas Math Symbols ± Lastly, we have the plus minus sign. We say plus or minus. 6± 2 http: //skola. bernkopf. cz jaroslav@bernkopf. cz 16

Mathematical Formulas Math Symbols Today’s Daily Dose of English is a request from Albert, in Catalunia, Spain. Albert has written: I recently saw the "Computer Symbols" video and thought it'd be really interesting [to have] a video about mathematic operations. For example, it took me some time to find out that 3 x 4 was read "three times four" (in Spanish we say "three by four"). There are plenty of them: 3+3, 3 -3, 3*3, 3/3, 3^3, sqrt(3), 3! and a lot more which I don't know how to write their symbols now. Many thanks for your videos!!! : -) Albert Mata. And many thanks to you, Albert, for making the request. It’s an excellent question and one that I’m sure many students are also unsure about. Unfortunately, Math was never my strong point. I’ve always been very good with English and always very bad with mathematics. However, if we avoid numbers and stick to the language, I should manage to explain this one reasonably well. From school, I remember the basic symbols that most people are familiar with, even if we're not particularly good at manipulating them. The most basic of these are. . . + - x ÷ = Let's start with the first one. This is the addition sign. We say it as plus or add. 1+2, 4+9. The next one is the subtraction sign. We say it as minus, or subtract, or take. 1 -2, 13 -12, 99 -7. Then we have the multiplication sign. We say this as times or multiplied by. 3 x 8, 26 x 3 The next is the division sign. I discovered that this is also called the obelus. You can also show division as /. We say this as divided by, or over. 3 ÷ 1, 10 ÷ 5, 6 / 3 The last of the common symbols is the equals sign. We say this as equals or is equal to. Other symbols I remember from my schooldays are. . . √ % π ° ∞ ± so we can look at these, too. This one is the square root. We say the square root of. √ 4 = 2 This one is the percentage sign. We say percent. 100% This one is Pi. This is a mathematical constant which begins 3. 141592653 and apparently has no end. This is an irrational number, apparently, though I have always been of the opinion that all numbers are irrational. People seem to be fascinated by Pi for the reason that it has no end. The only thing I remember about it is that the circumference of a circle equals π times its diameter, or something like that. The next symbol is the degree symbol. We say degrees. 90° 360° Then we have the symbol for infinity. That's about all I know of this one. Lastly, we have the plus minus sign. We say plus or minus. 6 ± 2. I have absolutely no idea why anyone would want to do this, but then again I teach English. My dislike of mathematics stems from my teacher making me stay in class at playtime because I couldn't memorize my multiplication tables when I was about 7 years old. I'm 7 x 7 now and I still don't know the multiplication tables by heart and I still don't like mathematics. So, I'm afraid that's the extent of my knowledge of mathematical symbols and the end of this Daily Dose of English. I hope you enjoyed it and I'll see you again soon for another one. Goodbye for now. http: //skola. bernkopf. cz jaroslav@bernkopf. cz 17

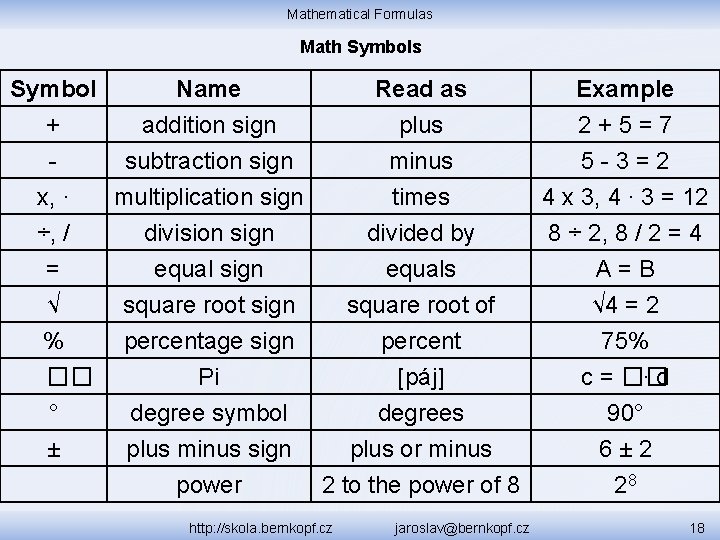
Mathematical Formulas Math Symbols Symbol Name + addition sign subtraction sign x, ∙ multiplication sign ÷, / = √ % �� ° ± division sign equal sign square root sign percentage sign Pi degree symbol plus minus sign power Read as plus minus times Example 2+5=7 5 -3=2 4 x 3, 4 ∙ 3 = 12 divided by equals square root of percent [páj] degrees plus or minus 2 to the power of 8 8 ÷ 2, 8 / 2 = 4 A=B √ 4 = 2 75% c = �� ∙d 90° 6± 2 28 http: //skola. bernkopf. cz jaroslav@bernkopf. cz 18

Mathematical Formulas Math Symbols List of mathematical symbols http: //en. wikipedia. org/wiki/List_of_mathematical_symbols http: //skola. bernkopf. cz jaroslav@bernkopf. cz 19

Mathematical Formulas The Tipping Point I give you a large piece of paper. Fold the paper over. Take that folded paper and fold it over again. Refold the original paper 50 times. How tall is the final stack? Most people guess: The pile would be as thick as a phone book, or it would be as tall as a refrigerator. The real height of the stack approximates the distance to the Sun. Folded it over one more time. The stack would be as high as the distance to the sun and back. This is called a geometric progression. Epidemics are another example of geometric progression. A virus spreads through a population. It doubles and doubles again. We have a hard time with this kind of progression. The end result is far out of proportion to the cause. http: //skola. bernkopf. cz jaroslav@bernkopf. cz 20

Mathematical Formulas The Tipping Point Malcolm Gladwell: The Tipping Point Consider, for example, the following puzzle. I give you a large piece of paper, and I ask you to fold it over once, and then take that folded paper and fold it over again, and then again, and again, until you have refolded the original paper 50 times. How tall do you think the final stack is going to be? In answer to that question, most people will fold the sheet in their mind's eye, and guess that the pile would be as thick as a phone book or, if they're really courageous, they'll say that it would be as tall as a refrigerator. But the real answer is that the height of the stack would approximate the distance to the Sun. And if you folded it over one more time, the stack would be as high as the distance to the sun and back. This is an example of what in mathematics is called a geometric progression. Epidemics are another example of geometric progression: when a virus spreads through a population, it doubles and doubles again, until it has (figuratively) grown from a single sheet of paper all the way to the Sun in fifty steps. As human beings we have a hard time with this kind of progression, because the end result — the effect — seems far out of proportion to the cause. http: //skola. bernkopf. cz jaroslav@bernkopf. cz 21

Mathematical Formulas The Tipping Point Odpovězte anglicky: 1. Jak vysoký by byl stoh přeložených papírů, kdybychom jeden papír přeložili 50 x? 2. Jak vysoký by byl stoh, kdybychom papír přeložili 51 x? 3. Popište, jak se množí virus. 6 x 3 Přeložte do angličtiny: 4. Dám ti velký kus papíru. 5. Stoh by byl vysoký jako lednička. 6. Znovu se zdvojnásobuje a zdvojnásobuje. http: //skola. bernkopf. cz jaroslav@bernkopf. cz 22

Mathematical Formulas Paper Magic http: //www. youtube. com/watch? v=N 1 s. Oc. D 2 v. ITQ http: //skola. bernkopf. cz jaroslav@bernkopf. cz 23

Mathematical Formulas A piece of string How long is a piece of string? http: //www. youtube. com/watch? v=oqc. Tspe 3 efc http: //skola. bernkopf. cz jaroslav@bernkopf. cz 24

Mathematical Formulas A piece of string Hello, how long is a piece of string? Here is a piece of string, a long piece of string. Here is another piece of string, so a medium length piece of string. And here is another piece of string, it's a short piece of string, or pieces of strings of different length. There‘s an expression in English which is „How long is a piece of string? " if you ask a question about a quantity, but given the information we have, there is no way to give an accurate answer: How long is it going to take to get there? How long is a piece of string? How much do you love me? How long is a piece of string? http: //skola. bernkopf. cz jaroslav@bernkopf. cz 25

Mathematical Formulas Q&A Thank you. Questions? http: //skola. bernkopf. cz jaroslav@bernkopf. cz 26

Mathematical Formulas Container beta times higher current – beta-krát větší proud calculate the current - vypočítat proud calculate the values – vypočítejte hodnoty Can you derive the equation? - Umíš odvodit ten vzorec? derive the equation - odvodit vzorec explain the equation - vysvětlit vzorec given the following conditions – jsou-li dány následující podmínky given the values - s danými hodnotami it consists of the sum. . . - skládá se ze součtu. . . many times - mnohokrát minus sign - znaménko mínus plus sign - znaménko plus resistance is equal to - odpor je roven resistance is zero – odpor je nulový simplify the above explanations – zjednodušit výše uvedená vysvětlení solve the task – řešit úlohu substitute the known values - dosadit známé hodnoty the gain is equal to zero – přenos je roven nule The gain is never lower than 1. - Zesílení nikdy menší než 1. the gain is reduced by 3 d. B − přenos je nižší o 3 d. B The output polarity is the same. - Výstupní polarita je ta samá. the output voltage is the same as the input voltage − výstupní napětí je stejné jako vstupní napětí the resistance is equal to - odpor je roven the resistance is practically infinite - odpor je prakticky nekonečný the voltage gain is equal to unity − napěťový přenos je roven jedné The voltage gain is infinite. - Napěťové zesílení je nekonečné. the voltages add together - napětí se sčítají this implies that - z toho vyplývá, že Children learn multiplication tables by heart. numbers_cardinal_ordinal. ppt model_numbers. ppt http: //skola. bernkopf. cz jaroslav@bernkopf. cz 27