Mathematical Analysis of Recursive Algorithms Design and Analysis

Example 1 Algorithm F(n) // compute n! recursively // input: a nonnegative integer n

Exp 1: Analysis (1) Input size = n Formula: F(n) = F(n-1) * n;

Exp 1: Analysis (2) Solving recurrence relations: Method of backward substitution M(n) = M(n-1)

Analyzing Efficiency of Recursive Algorithms (1) 1. Decide on a parameter(s) indicating an input’s

Analyzing Efficiency of Recursive Algorithms (2) 4. Set up a recurrence relation, with an

Example 2: Tower of Hanoi (1) n disks on different sizes and three pegs

Example 2: Tower of Hanoi (2) CS 3024 -FAZ 8

Tower of Hanoi: Recursive Solution (1) CS 3024 -FAZ 9

To. H: Recursive Solution (2) To move n>1 disks from peg 1 to peg

Exp 2: Analysis (1) Input’s size = the number of disks = n Basic

Exp 2: Analysis (2) Backward substitution: M(n) = 2 M(n-1) + 1 = 2[2

Exp 2: Analysis (3) Initial condition, n=1 i=n-1: M(n) = 2 i. M(n-i) +

Example 3 Algorithm Bin. Rec(n) //input: a positive decimal integer n //output: the number

Exp 3: Analysis (1) The number of additions A(n) = A( n/2 ) +

Exp 3: Analysis (2) Use smoothness rule: under the very broad assumptions the order

Exp 3: Analysis (3) Use backward substitution: A(2 k) = A(2 k-1) + 1

Exp 3: Analysis (4) A(2 k) = A(1) + k = k n =

Exercises Solve the following recurrence relations: x(n)=x(n-1)+5 for n>1, x(1)=0 x(n)=3 x(n-1)+5 for n>1,

Slides: 19

Download presentation

Mathematical Analysis of Recursive Algorithms Design and Analysis of Algorithms (CS 3024) 28/02/2006 CS 3024 -FAZ 1

Example 1 Algorithm F(n) // compute n! recursively // input: a nonnegative integer n // output: the value of n! if n = 0 return 1 else return F(n-1)*n CS 3024 -FAZ 2

Exp 1: Analysis (1) Input size = n Formula: F(n) = F(n-1) * n; n>0 F(0) = 1 The number of multiplication M(n) = M(n-1) + 1; n>0 if n = 0 return 1 The call stops when n = 0 M(0) = 0 initial condition CS 3024 -FAZ 3

Exp 1: Analysis (2) Solving recurrence relations: Method of backward substitution M(n) = M(n-1) + 1 = [M(n-2)+1] + 1 = M(n-2) + 2 = [M(n-3)+1] + 2 = M(n-3) + 3 General formula pattern: M(n)=M(n-i) + i Initial condition, n=0 i = n: M(n)= M(n-1)+1 = M(n-2)+2 =…= M(n-n)+n = n CS 3024 -FAZ 4

Analyzing Efficiency of Recursive Algorithms (1) 1. Decide on a parameter(s) indicating an input’s size 2. Identify the algorithm’s basic operation (typically, it is located in its inner most loop) 3. Check whether the number of times the basic operation is executed depends only on the size of an input. If it also depend on some additional property, the worst-case, average-case, and, if necessary, the best-case efficiencies have to be investigated separately CS 3024 -FAZ 5

Analyzing Efficiency of Recursive Algorithms (2) 4. Set up a recurrence relation, with an appropriate initial condition, for the number of times the algorithm’s basic operation is executed 5. Solve the recurrence or at the least ascertain(memastikan) the order of growth of its solution CS 3024 -FAZ 6

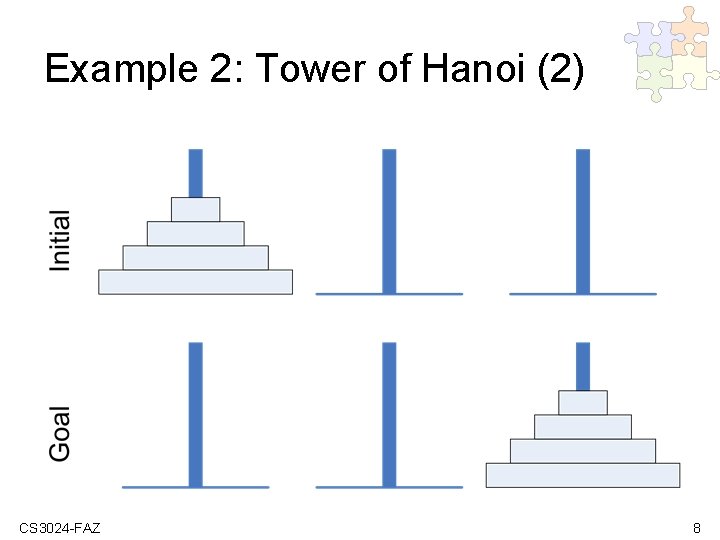
Example 2: Tower of Hanoi (1) n disks on different sizes and three pegs Initially, all disks are on the first peg in order of size. The largest on the bottom and the smallest on top The goal: move all disks to the third peg, using the second one as an auxiliary Move only one disk at a time It is forbidden to place a larger disk on top of a smaller one CS 3024 -FAZ 7

Example 2: Tower of Hanoi (2) CS 3024 -FAZ 8

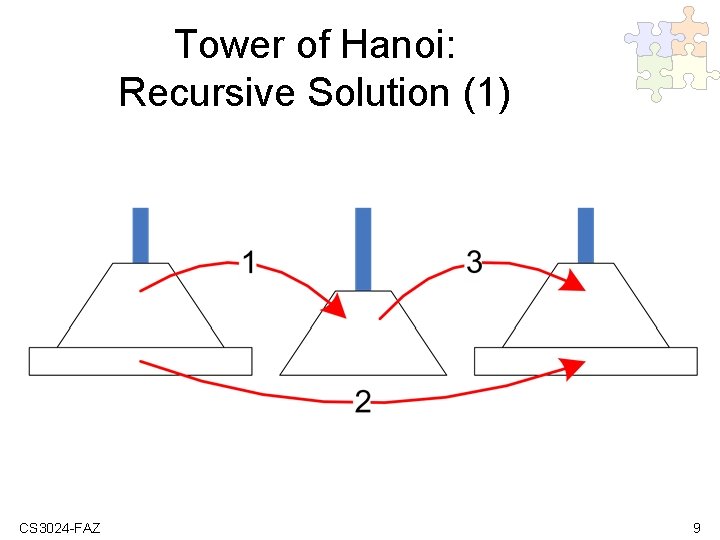
Tower of Hanoi: Recursive Solution (1) CS 3024 -FAZ 9

To. H: Recursive Solution (2) To move n>1 disks from peg 1 to peg 3 (with peg 2 as an auxiliary(alat bantu)): Move recursively n-1 disk(s) from peg 1 to peg 2 (with peg 3 as an auxiluiary) Move the largest disk from peg 1 to peg 3 Move recursively n-1 disk(s) from peg 2 to peg 3 (with peg 1 as an auxiliary) CS 3024 -FAZ 10

Exp 2: Analysis (1) Input’s size = the number of disks = n Basic operation = moving one disk The number of moves M(n) depends on n only: M(n) = M(n-1) + 1 + M(n-1) ; for n>1 Recurrence relation: M(n) = 2 M(n-1) + 1 ; for n>1 M(1) = 1 initial condition CS 3024 -FAZ 11

Exp 2: Analysis (2) Backward substitution: M(n) = 2 M(n-1) + 1 = 2[2 M(n-2)+1]+1=22 M(n-2)+2+1 = 22 [2 M(n-3)+1]+2+1=23 M(n-3)+22+2+1 = 24 M(n-4)+23+22+2+1 The pattern, after i substitution: M(n) = 2 i. M(n-i) + 2 i-1 + 2 i-2 +. . + 2 + 1 = 2 i. M(n-i) + 2 i - 1 CS 3024 -FAZ 12

Exp 2: Analysis (3) Initial condition, n=1 i=n-1: M(n) = 2 i. M(n-i) + 2 i - 1 = 2(n-1)M(n-(n-1)) + 2(n-1) -1 = 2(n-1)M(1) + 2(n-1) - 1 = 2(n-1) + 2(n-1) - 1 = 2 n - 1 Exponential algorithm! This is the most efficient algorithm It is the problem’s intrinsic difficulty that makes it so computationally difficult CS 3024 -FAZ 13

Example 3 Algorithm Bin. Rec(n) //input: a positive decimal integer n //output: the number of binary digits in n’s binary // representation if n = 1 return 1 else return Bin. Rec( n/2 ) + 1 CS 3024 -FAZ 14

Exp 3: Analysis (1) The number of additions A(n) = A( n/2 ) + 1 ; for n>1 Recursive calls end n=1, initial condition: A(1) = 0 The presence of n/2 backward substitution stumble on values of n that are not powers of 2  CS 3024 -FAZ 15

Exp 3: Analysis (2) Use smoothness rule: under the very broad assumptions the order of growth for n=2 k ≈ the order of growth for all values of n n = 2 k : A(2 k) = A(2 k-1) + 1 ; for n>1 A(20) = 0 CS 3024 -FAZ 16

Exp 3: Analysis (3) Use backward substitution: A(2 k) = A(2 k-1) + 1 = [A(2 k-2) + 1] + 1 = A(2 k-2) + 2 = [A(2 k-3) + 1] + 2 = A(2 k-3) + 3 … = A(2 k-i) + i … = A(2 k-k) + k = A(1) + k = k CS 3024 -FAZ 17

Exp 3: Analysis (4) A(2 k) = A(1) + k = k n = 2 k, k = log 2 n A(n) = log 2 n (log n) The exact solution (more refined formula) A(n) = log 2 n CS 3024 -FAZ 18

Exercises Solve the following recurrence relations: x(n)=x(n-1)+5 for n>1, x(1)=0 x(n)=3 x(n-1)+5 for n>1, x(1)=4 x(n)=x(n-1)+n for n>0, x(0)=0 x(n)=x(n/2)+n for n>1, x(1)=1 (solve for n=2 k) x(n)=x(n/3)+1 for n>1, x(1)=1 (solve for n=3 k) CS 3024 -FAZ 19