MATHEMATICA L REASONING STATEMENT A SENTENCE EITHER TRUE


















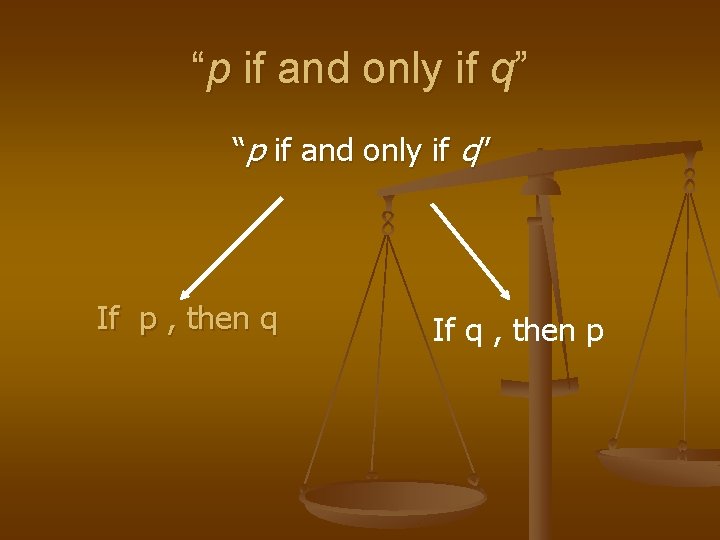


























- Slides: 49

MATHEMATICA L REASONING

STATEMENT A SENTENCE EITHER TRUE OR FALSE BUT NOT BOTH

STATEMENT n n TEN IS LESS THAN ELEVEN STATEMENT ( TRUE ) TEN IS LESS THAN ONE STATEMENT ( FALSE) PLEASE KEEP QUIET IN THE LIBRARY NOT A STATEMENT

no Sentence 1 123 is divisible by 3 2 statement Not statement reason true false 3 X-2 ≥ 9 4 Is 1 a prime number? 5 All octagons have eight sides Neither true or false A question true

QUANTIFIERS n n n USED TO INDICATE THE QUANTITY ALL – TO SHOW THAT EVERY OBJECT SATISFIES CERTAIN CONDITIONS SOME – TO SHOW THAT ONE OR MORE OBJECTS SATISFY CERTAIN CONDITIONS

QUANTIFIERS EXAMPLE : - All cats have four legs Some even numbers are divisible by 4 All perfect squares are more than 0

OPERATIONS ON SETS NEGATION The truth value of a statement can be changed by adding the word “not” into a statement. TRUE FALSE

NEGATION EXAMPLE P : 2 IS AN EVEN NUMBER ( TRUE ) P (NOT P ) : 2 IS NOT AN EVEN NUMBER (FALSE )

COMPOUND STATEMENT

COMPOUND STATEMENT A compound statement is formed when two statements are combined by using n n “Or” “and”

COMPOUND STATEMENT P Q P AND Q TRUE FALSE TRUE FALSE

COMPOUND STATEMENT P TRUE Q TRUE P OR Q TRUE FALSE FALSE TRUE

COMPOUND STATEMENT EXAMPLE : P : All even numbers can be divided by 2 ( TRUE ) Q : -6 > -1 ( FALSE ) P and Q : FALSE

COMPOUND STATEMENT P : All even numbers can be divided by 2 ( TRUE ) Q : -6 > -1 ( FALSE ) P OR Q TRUE :

IMPLICATIONS n SENTENCES IN THE FORM where And ‘ If p then q ’ , p and q are statements p is the antecedent q is the consequent

IMPLICATIONS Example : If x 3 = 64 , then x = 4 Antecedent : x 3 = 64 Consequent : x = 4

IMPLICATIONS Example : Identify the antecedent and consequent for the implication below. “ If the whether is fine this evening, then I will play football” Answer : Antecedent : the whether is fine this evening Consequent : I will play football

“p if and only if q” The sentence in the form “p if and only if q” , is a compound statement containing two implications: a) If p , then q b) If q , then p
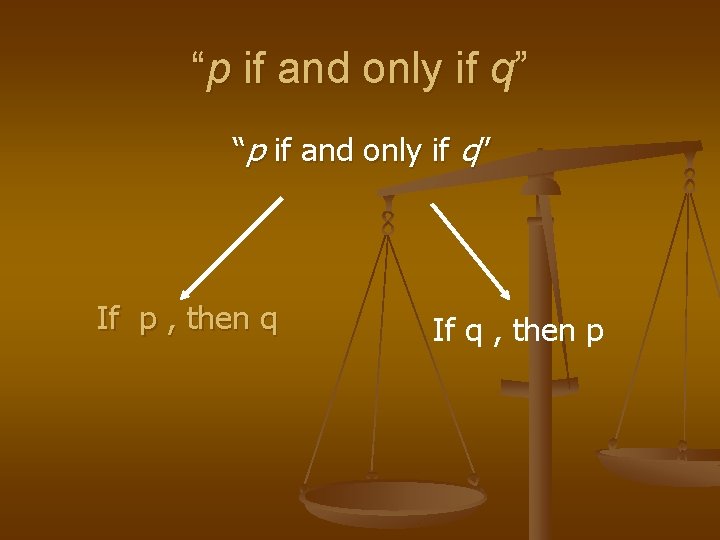
“p if and only if q” If p , then q If q , then p

Homework !!!! n Pg: 96 No 1 and 2 98 No 1, 2 ( b, c ) 4 ( a, b, c, d)

IMPLICATIONS The converse of “If p , then q” is “if q , then p”.

IMPLICATIONS Example : If x = -5 , then 2 x – 7 = -17

Mathematical reasoning Arguments



ARGUMENTS What is argument ? - A process of making conclusion based on a set of relevant information. - Simple arguments are made up of two premises and a conclusion

ARGUMENTS Example : All quadrilaterals have four sides. A rhombus is a quadrilateral. Therefore, a rhombus has four sides.

ARGUMENTS n There are three forms of arguments :

Argument Form I ( Syllogism ) Premise 1 : All A are B Premise 2 : C is A Conclusion : C is B

ARGUMENTS Argument Form 1( Syllogism ) Make a conclusion based on the premises given below: Premise 1 : All even numbers can be divided by 2 Premise 2 : 78 is an even number Conclusion : 78 can be divided by 2

ARGUMENTS Argument Form II ( Modus Ponens ): Premise 1 : If p , then q Premise 2 : p is true Conclusion : q is true

ARGUMENTS Example Premise 1 : If x = 6 , then x + 4 = 10 Premise 2 : x = 6 Conclusion : x + 4 = 10

ARGUMENTS Argument Form III (Modus Tollens ) Premise 1 : If p , then q Premise 2 : Not q is true Conclusion : Not p is true

ARGUMENTS Example : Premise 1 : If ABCD is a square, then ABCD has four sides Premise 2 : ABCD does not have four sides. Conclusion : ABCD is not a square

ARGUMENTS Completing the arguments n n recognise the argument form Complete the argument according to its form

ARGUMENTS Example Premise 1 : All triangles have a sum of interior angles of 180 PQR is a triangle Premise 2 : ______________ Conclusion : PQR has a sum of interior Argument Form I angles of 180

ARGUMENTS Premise 1 : If x - 6 = 10 , then x = 16 x – 6 = 10 Premise 2 : _____________ Conclusion : x Argument = 16 Form II

ARGUMENTS Premise 1 : If x divisible by 2 , then x is an even number _____________ Premise 2 : x is not an even number Conclusion : Argument x is not Form divisible by 2 III

ARGUMENTS Homework : Pg : 103 Ex 4. 5 No 2, 3, 4, 5

MATHEMATICAL REASONING DEDUCTION AND INDUCTION



REASONING n There are two ways of making conclusions through reasoning by a) Deduction b) Induction

DEDUCTION IS A PROCESS OF MAKING A SPECIFIC CONCLUSION BASED ON A GIVEN GENERAL STATEMENT

DEDUCTION Example : general All students in Form 4 X are present today. David is a student in Form 4 X. Conclusion : David is present today Specific

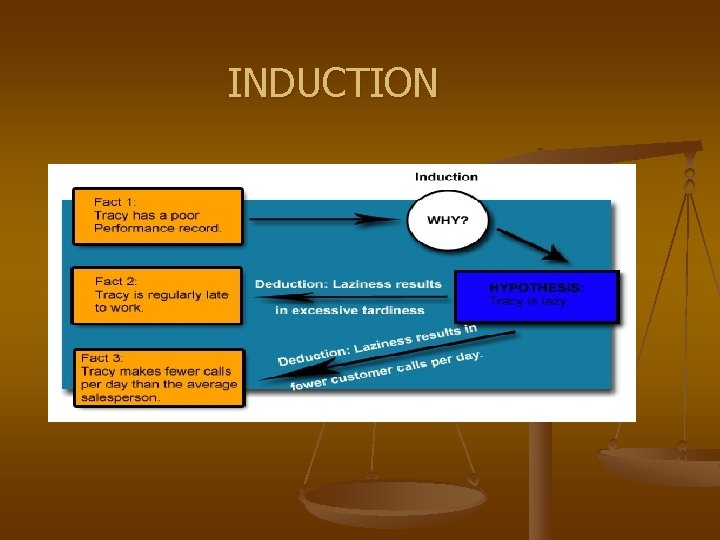
INDUCTION A PROCESS OF MAKING A GENERAL CONCLUSION BASED ON SPECIFIC CASES.

INDUCTION

INDUCTION Amy is a student in Form 4 X. Amy likes Physics Carol is a student in Form 4 X. Carol likes Physics Elize is a student in Form 4 X. Elize likes Physics …………………………. . Conclusion : All students in Form 4 X like Physics.

REASONING Deduction GENERAL SPECIFIC Induction