Math Success Project Using Data to Improve Student

Math Success Project: Using Data to Improve Student Achievement in College-Level Mathematics Ron Henry, Georgia State University Danette Gerald, The Education Trust

Background and History of Mathematics Success Project 03/17/08 2

Nine States in Math Success o NASH/Education Trust n n n n n 03/17/08 State University System of Florida University System of Georgia University of Hawaii System Purdue University (Indiana) Kentucky Council on Postsecondary Ed. University of Louisiana System Mississippi Institutions of Higher Learning Nevada System of Higher Education State University of New York (SUNY) 3

Research Question o What factors/strategies increase success of students in college mathematics courses? n n 03/17/08 Success definition – number of starters who complete the course with a least a grade of C [or P (if P/F) or S (if S/U)] For a predictor, success definition – 75% chance of at least a grade of C 4

Core Analyses o Student retention/success in each course n n n % of starters successful (ABC; P; S) % of starters with W % of completers successful (ABC; P; S) o Student preparation or placement in a course n n n 03/17/08 ACT/SAT data and success HS courses and success Correlation of placement tests 5

Core Analyses o Student retention/success in each course n n 03/17/08 For fall 2005 and spring 2006 By course; remedial; terminal math; college algebra; pre-calculus; calculus By sector [2 -year; comprehensive; research] By race/ethnicity 6

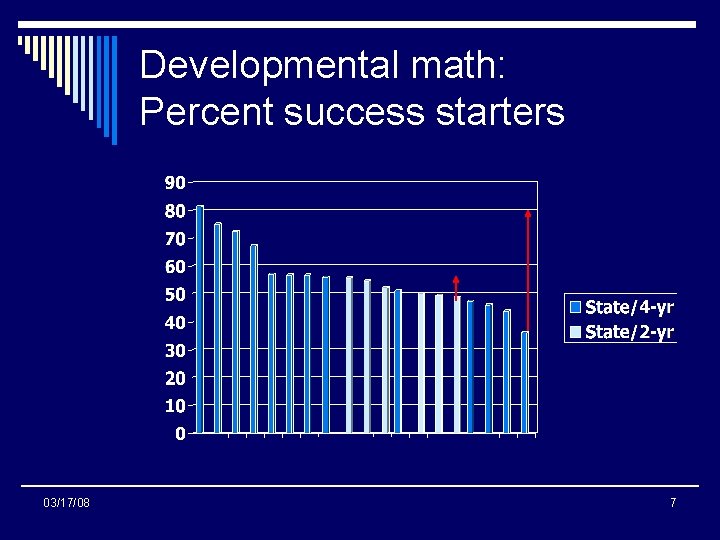
Developmental math: Percent success starters 03/17/08 7

College Algebra: Percent success starters 03/17/08 8

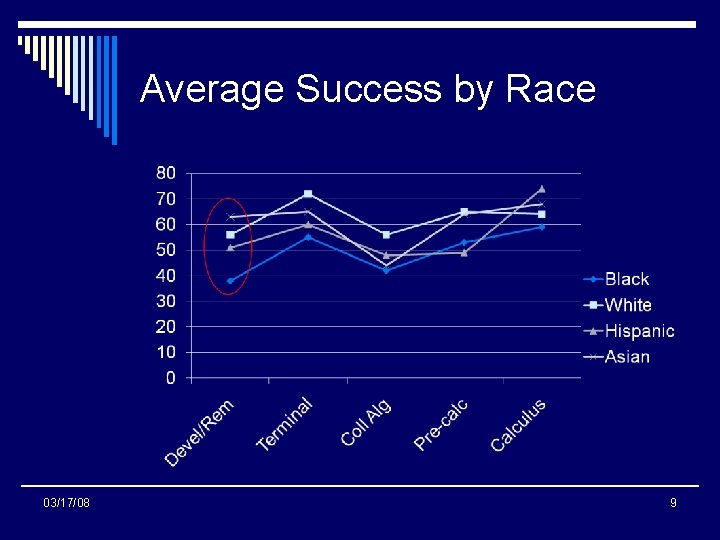
Average Success by Race 03/17/08 9

Core Analysis I: Conclusions n Wide range of success p. Across the various Systems and sectors p. Within the same System and sector p. Among sections within the same institution p. Across ethnicities – significant gaps n 03/17/08 Some institutions have much higher success rates => Let’s learn from them 10

Core Analysis II: % Freshmen taking math courses o Range: 41. 7% - 85. 9% [Median 70. 2%] o Surprised that a large percentage of freshmen do not take any math courses in their first year o => Policy implication: Should all freshmen be required to attempt math course in their first year? 03/17/08 11

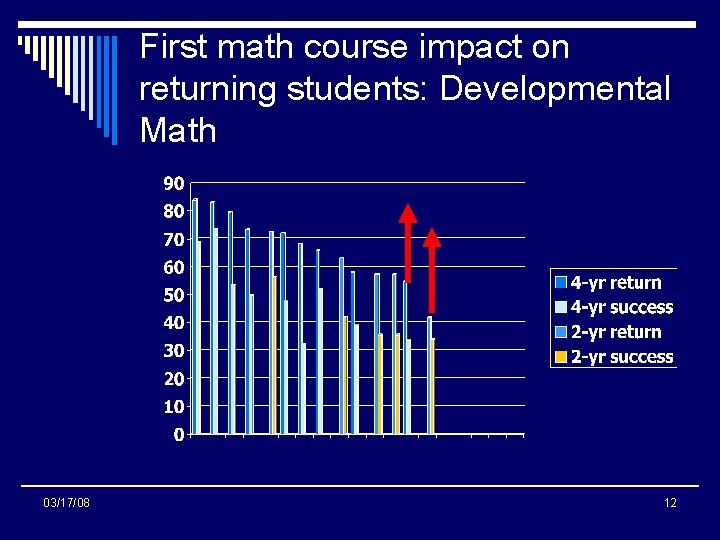
First math course impact on returning students: Developmental Math 03/17/08 12

First math course impact on returning students: College Algebra 03/17/08 13

First math course impact on returning students: Conclusions o Many students return who have not been successful in their first-year math courses o => Reinforces policy implication of requiring students to take math in their first year 03/17/08 14

High School Preparation How can we work with [high] schools to help more students be successful in K-12 mathematics so that they are prepared for non-remedial mathematics college courses, i. e. test out of Elementary Algebra [Developmental/remedial math]? 03/17/08 What percentage of your First Year students completed high school taking less than Algebra II? What percentage completed at least Algebra II? What percentage completed more than Algebra II? How does that preparation correlate with college mathematics readiness? 15

HS math courses taken in 12 th grade by entering college freshmen # students < Algebra II Other int. math Pre-calc Calculus AP calculus IB math Other adv math No 12 th math 03/17/08 % students 316 3. 7% 73 0. 9% 426 5. 0% 1862 295 729 558 31 3151 1020 22. 0% 3. 5% 8. 6% 6. 6% 0. 4% 37. 2% 12. 1% 16

HS math & College Success % 03/17/08 17

Conclusions o Regardless of HS math preparation, students placed in remedial math have low probability of success o Preparation in HS matters, however just looking at the course taken in 12 th grade is not sufficient for analysis o => Should ask the question: “ What is the highest level mathematics course in HS in which the student was successful? ” 03/17/08 18

Core Analyses o Placement exams and success in course n Predictability of ACT/SAT scores and success o Pre-requisite course and success in next course 02/13/07 03/17/08 19

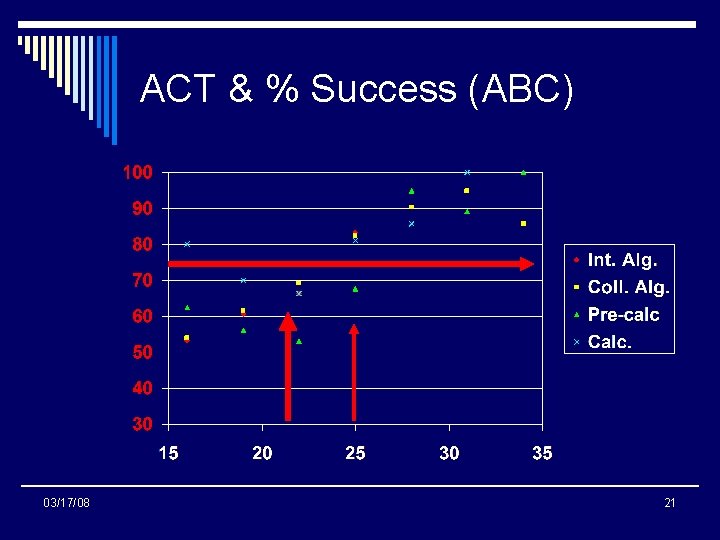
ACT Math benchmark o ACT Math benchmark for success in College Algebra is 22 o Where success is defined as a 50% probability of obtaining a grade of B or better o Used logistic regression model 03/17/08 20

ACT & % Success (ABC) 03/17/08 21

SAT & % Success (ABC) 03/17/08 22

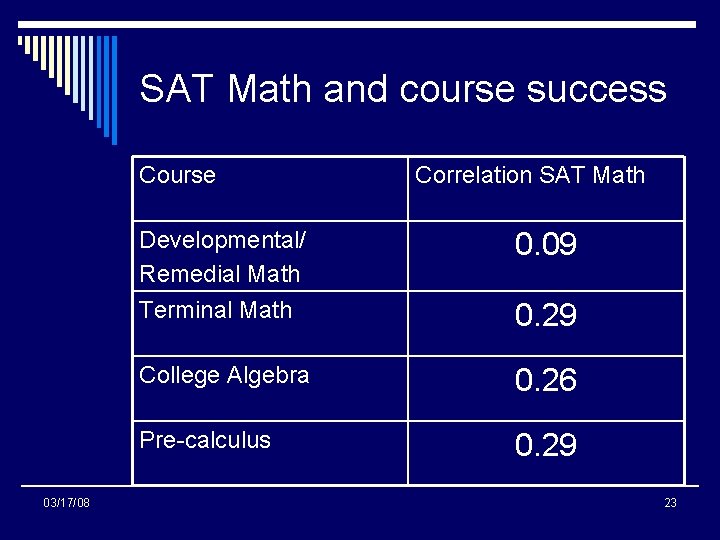
SAT Math and course success Course 03/17/08 Correlation SAT Math Developmental/ Remedial Math 0. 09 Terminal Math 0. 29 College Algebra 0. 26 Pre-calculus 0. 29 23

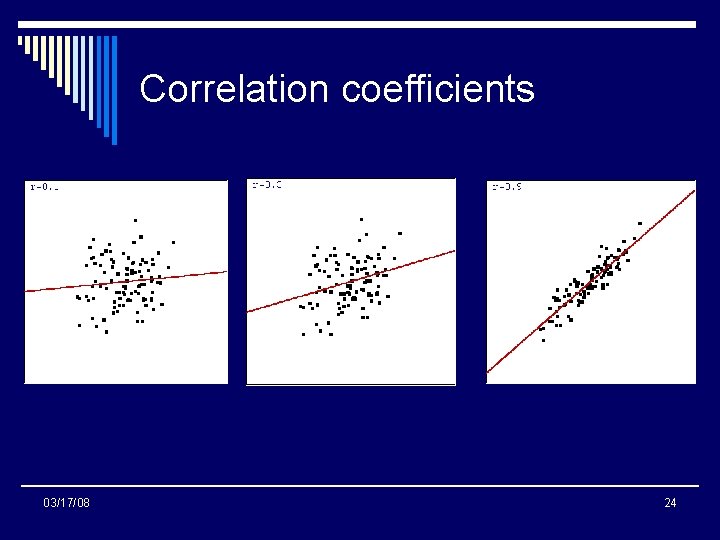
Correlation coefficients 03/17/08 24

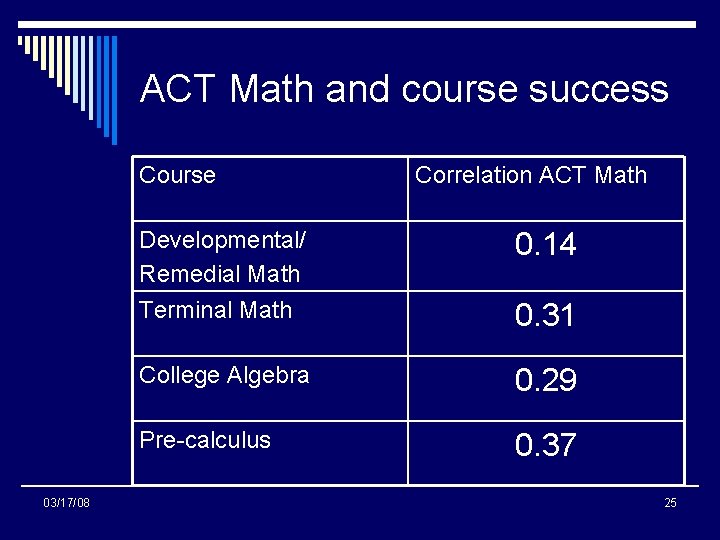
ACT Math and course success Course 03/17/08 Correlation ACT Math Developmental/ Remedial Math 0. 14 Terminal Math 0. 31 College Algebra 0. 29 Pre-calculus 0. 37 25

Conclusion ACT Math appears to be a better predictor of success than SAT Quantitative, but the correlation is fairly weak 02/13/07 03/17/08 26

Placement If many students who test into a mathematics course are not being successful in this course, how do we change the screening test? Are there particular topics in which many students are struggling? Are there student characteristics that correlate with success? o COMPASS 36 < Alge < 50 -> 79% ABC college algebra o COMPASS 30 < Trig < 45 -> 64% ABC pre-calculus o COMPASS Trig > 45 -> 79% ABC calculus I 02/13/07 03/17/08 27

Placement If a student passes your prerequisite mathematics course with a C or better, what should be a goal for success in their current mathematics course? What is the success of students in subsequent mathematics courses as a function of their grade in the first mathematics course? o ABC college algebra -> 59% ABC pre-calculus o ABC pre-calculus -> 54% ABC calculus 02/13/07 03/17/08 28

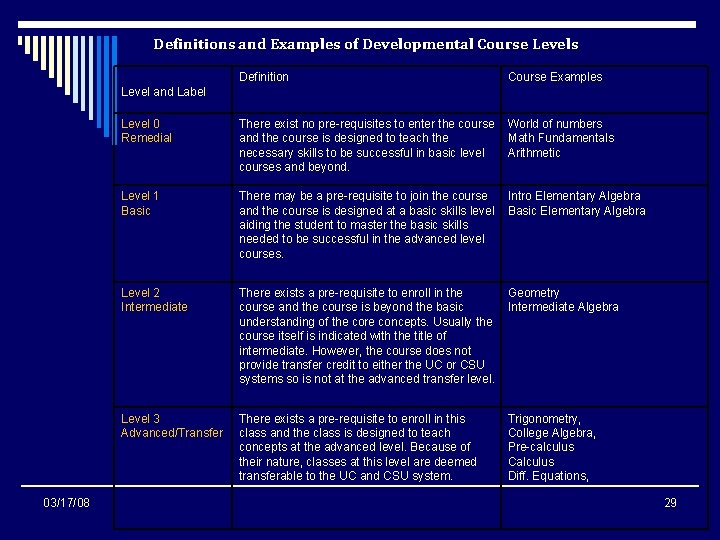
Definitions and Examples of Developmental Course Levels Definition Course Examples Level 0 Remedial There exist no pre-requisites to enter the course and the course is designed to teach the necessary skills to be successful in basic level courses and beyond. World of numbers Math Fundamentals Arithmetic Level 1 Basic There may be a pre-requisite to join the course and the course is designed at a basic skills level aiding the student to master the basic skills needed to be successful in the advanced level courses. Intro Elementary Algebra Basic Elementary Algebra Level 2 Intermediate There exists a pre-requisite to enroll in the course and the course is beyond the basic understanding of the core concepts. Usually the course itself is indicated with the title of intermediate. However, the course does not provide transfer credit to either the UC or CSU systems so is not at the advanced transfer level. Geometry Intermediate Algebra Level 3 Advanced/Transfer There exists a pre-requisite to enroll in this class and the class is designed to teach concepts at the advanced level. Because of their nature, classes at this level are deemed transferable to the UC and CSU system. Trigonometry, College Algebra, Pre-calculus Calculus Diff. Equations, Level and Label 03/17/08 29

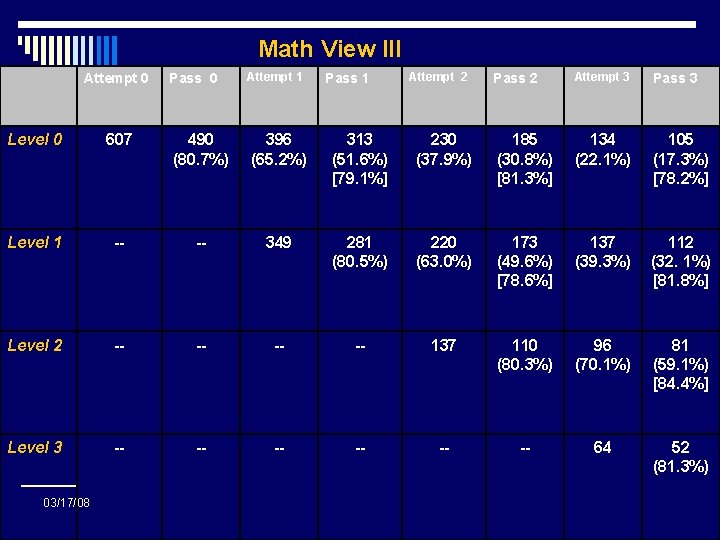
Math View III Attempt 0 Pass 0 Attempt 1 Pass 1 Attempt 2 Pass 2 Attempt 3 Pass 3 Level 0 607 490 (80. 7%) 396 (65. 2%) 313 (51. 6%) [79. 1%] 230 (37. 9%) 185 (30. 8%) [81. 3%] 134 (22. 1%) 105 (17. 3%) [78. 2%] Level 1 -- -- 349 281 (80. 5%) 220 (63. 0%) 173 (49. 6%) [78. 6%] 137 (39. 3%) 112 (32. 1%) [81. 8%] Level 2 -- -- 137 110 (80. 3%) 96 (70. 1%) 81 (59. 1%) [84. 4%] Level 3 -- -- -- 64 52 (81. 3%) 03/17/08 30

Interventions o Supplemental Instruction (SI) o Course Redesign* n Emporium Model (Virginia Tech) n Fully Online Model (Iowa State) n Replacement Model (U of Alabama) n Supplemental Model (Carnegie Mellon) n Buffet Model (Mohave CC) *Twigg, C. A. (2003). “Improving Learning & Reducing Costs: Redesigning Large-Enrollment Courses. ” Educause Review 38(5): 28 -36. 03/17/08 31

Interventions o Course Redesign n Replacement Model n n 03/17/08 U of Alabama; LSU; U of Idaho Recommend 1 hour classroom + 3 hours in math lab 32

Persistence What is the retention and graduation success of your mathematics under-prepared students? How many students who have to repeat their first mathematics course do not enroll for their second year? Are under-prepared students when placed in credit-bearing math courses instead of developmental/remedial courses experiencing success? 02/13/07 03/17/08 33

Conclusions o Large number of remedial students are not successful o Non-remedial students are also not particularly successful, even in Calculus o => Need to examine what we mean by readiness for College Algebra or Calculus OR “What are the standards for entrance and exit from a particular mathematics course? ” 02/13/07 03/17/08 34

Policy Ideas o Students can drop and re-enroll at will. n Can we at least ask them why? ? o Students allow long time intervals between steps. n Can we encourage them to be continuously enrolled? o Students do not understand the relationship and importance of math. n How can we stress the importance of specific courses? o Students fear math n Can we de-mystify it? p Non-graded p Applied p Learning communities 03/17/08 35

Data to monitor o Student retention/success in each course n % of starters successful n % of starters who withdraw o Student success in subsequent math course o Student success if placed in course o Variations in student success across sections of same course o Gaps in success for various ethnicities 03/17/08 36

Mathematics Success Project: Data Collection and Analysis Ronald J Henry Georgia State University 03/17/08 37

Community College University Transfer Rates n Difficult to get ACCURATE information p n California picture p p n n No national data About 40% of first-time students in the California community colleges are not seeking a degree or certificate, but are pursuing basic skills, job skills, or personal enrichment. Of the 60% who are seeking a degree or certificate, only about 1/4 succeed in transferring to a university and/or earning an associate’s degree or a certificate within six years. Dr. Linda Serra Hagedor (University of Florida) Dr. Alberto Cabrera (University of Maryland) Shulock, N. & Moore, C. (2007) Rules of the Game: How State Policy Creates Barriers to Degree Completion and Impedes Student Success in the California Community College 03/17/08 38