Math Review with Matlab Laplace Transform Calculating the

Math Review with Matlab: Laplace Transform Calculating the Inverse Laplace Transform S. Awad, Ph. D. M. Corless, M. S. E. E. E. C. E. Department University of Michigan-Dearborn

X(s) Laplace Transform: Inverse Laplace Transform § § § Laplace Nomenclature Table Look Up Method Simple Table Look Up Example Inverse Laplace Transform General Form Distinct Pole Example Repeated Poles Example 2

X(s) Laplace Transform: Inverse Laplace Transform Laplace Nomenclature § The Laplace Transform of a time domain function x(t), will be a complex domain function X(s) § This relationship is also denoted as: 3

X(s) Laplace Transform: Inverse Laplace Transform § Inverse Laplace Transform is used to compute x(t) from X(s) § The Inverse Laplace Transform is strictly defined as: § Strict computation is complicated and rarely used in engineering § Practically, the Inverse Laplace Transform of a rational function is calculated using a method of table look-up 4

X(s) Laplace Transform: Inverse Laplace Transform Table Look Up Method § If X(s) can be written as a sum of terms with known Inverse Laplace Transforms, x(t) will be the sum of these Inverse Laplace Transforms § Requires knowledge or reference of Laplace Transform pairs, but is much simpler than directly calculating the Inverse Laplace Transform 5

X(s) Laplace Transform: Inverse Laplace Transform Simple Table Look Up Example § Given: § Use superposition and the Table Look-Up Method determine the Inverse Laplace Transform of X(s) § Verify the result using Matlab 6

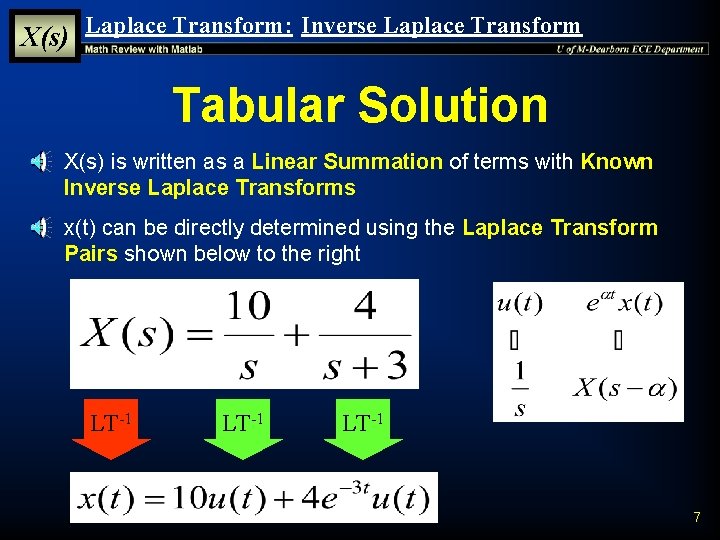
X(s) Laplace Transform: Inverse Laplace Transform Tabular Solution § X(s) is written as a Linear Summation of terms with Known Inverse Laplace Transforms § x(t) can be directly determined using the Laplace Transform Pairs shown below to the right LT-1 7

X(s) Laplace Transform: Inverse Laplace Transform Matlab Verification § The ilaplace Matlab command can be used to quickly verify the solution » syms X s » X=((10/s)+(4/(s+3))); » x=ilaplace(X) x = 10+4*exp(-3*t) § NOTE: The output of ilaplace must be interpreted as a Causal Solution 8

X(s) Laplace Transform: Inverse Laplace Transform General Form § In general X(s) can be written as a rational function z 1, z 2, … , zm are the zeros of X(s) p 1, p 2, … , pn are the poles of X(s) § If X(s) is written as a strictly rational function, a method using partial-fraction expansion can be used to determine the inverse Laplace transform 9

X(s) Laplace Transform: Inverse Laplace Transform Strictly Rational Function § A function X(s) is strictly rational if the Degree of its Numerator Polynomial N(s) is Less than the Degree of its Denominator Polynomial D(s) § If N(s) ³ D(s), perform Long Division until the remainder polynomial R(s) is of lesser order than A(s) N(s) = Numerator D(s) = Denominator Q(s) = Quotient R(s) = Remainder 10

X(s) Laplace Transform: Inverse Laplace Transform Partial-Fraction Expansion based on Poles § Once X(s) is written in a strictly rational form, Partial Fraction Expansion can be performed § Partial-Fraction Expansion of of X(s) can be classified into two categories based on the Poles of X(s) § CASE I: All Poles are Distinct § CASE II: All or Some Poles are Repeated 11

X(s) Laplace Transform: Inverse Laplace Transform CASE 1: Distinct Poles § Assume that all Poles are Different ( pi pj if i j ) § Assume numerator order is less than denominator order, then the Partial Fraction Expansion of X(s) is given by: where: 12

X(s) Laplace Transform: Inverse Laplace Transform LT-1 of Distinct Terms § X(s) can be written as the sum of terms § Due to the Linearity Property, x(t) will be the sum of the Inverse Laplace Transform of the terms § Building from previous work, x(t) is the summation of unit steps multiplied by exponentials 13

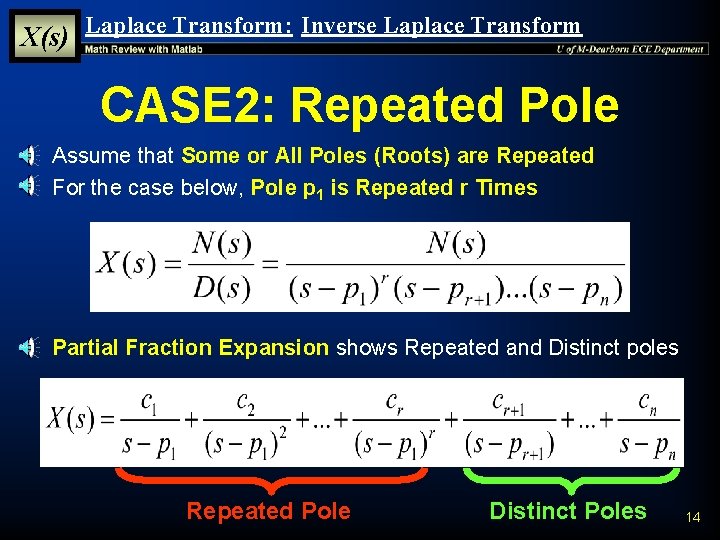
X(s) Laplace Transform: Inverse Laplace Transform CASE 2: Repeated Pole § Assume that Some or All Poles (Roots) are Repeated § For the case below, Pole p 1 is Repeated r Times § Partial Fraction Expansion shows Repeated and Distinct poles Repeated Pole Distinct Poles 14

X(s) Laplace Transform: Inverse Laplace Transform Determine Coefficients § Find Distinct Poles Coefficients, i = r+1, r+2, . . . , n § Find First Repeated Pole Coefficient, i = r § Find General Repeated Poles, i = 1, 2, . . . , r-1 15

X(s) Laplace Transform: Inverse Laplace Transform Partial-Fraction Expansion Method for Determining Inverse Laplace Transform Put Rational Function into Strictly Rational Form where the degree of the numerator polynomial less than that of the denominator polynomial Factor the Denominator Polynomial Perform Partial-Fraction Expansion Use Laplace Transform Pair Table to obtain the inverse Laplace transform 16

X(s) Laplace Transform: Inverse Laplace Transform Distinct Pole Example § Given: § Use the Partial-Fraction Expansion and the Table Look-Up Method determine the Inverse Laplace Transform of X(s) § Verify the result using Matlab § Order of Numerator (2) < Order of Denominator (3) § Notice all Poles are Distinct 17

X(s) Laplace Transform: Inverse Laplace Transform Partial Fraction Expansion § Start by finding Partial Fraction Expansion of X(s) § Poles of p 1=-1, p 2=-2, p 3=-3 Partial Fraction Expansion § Find ci coefficients 18

X(s) Laplace Transform: Inverse Laplace Transform Find Coefficient C 1 § Each coefficient is determined by evaluating: § c 1 is explicitly evaluated as: C 1 = -2 19

X(s) Laplace Transform: Inverse Laplace Transform Find Coefficient C 2 and C 3 C 2 = 3 C 3 = 1 20

X(s) Laplace Transform: Inverse Laplace Transform Partial Fraction Expanded X(s) § Original Expression § Expansion § Replace with Coefficients 21

X(s) Laplace Transform: Inverse Laplace Transform § x(t) = Sum of the Inverse Laplace Transform of the individual terms of X(s) LT-1 22

X(s) Laplace Transform: Inverse Laplace Transform Distinct Pole Matlab Verification § This can easily be verified in Matlab using ilaplace » syms Xnum Xden s » Xnum = 2*s^2 -s +5; % Numerator X(s) » Xden = (s+1)*(s+2)*(s-3); % Denominator » x = ilaplace( Xnum/Xden ) x = -2*exp(-t)+3*exp(-2*t)+exp(3*t) 23

X(s) Laplace Transform: Inverse Laplace Transform Repeated Pole Example § Given: § Order of Numerator (4) = Order of Denominator (4) therefore X(s) is NOT Strictly Rational § Notice Pole s = -2 is Repeated 3 times § Use the Partial-Fraction Expansion and the Table Look-Up Method determine the Inverse Laplace Transform of X(s) § Verify each step using Matlab 24

X(s) Laplace Transform: Inverse Laplace Transform Solution Steps § Convert X(s) to a strictly rational function Perform long division by hand u Verify long division using Matlab deconv u § Perform partial fraction expansion on rational part of X(s) Calculate coefficients by hand u Calculate coefficients in Matlab using diff and subs u § Verify conversion to strictly rational function using combination of int and diff commands § Use table method to determine Inverse Laplace Transform § Verify entire process using ilaplace 25

X(s) Laplace Transform: Inverse Laplace Transform Repeated Pole Example § X(s) must be decomposed into a constant plus a Strictly Rational Function § Q(s) will just be a constant since the order of the numerator and the denominator are the same 26

X(s) Laplace Transform: Inverse Laplace Transform Convert to Rational Functions § Must Decompose X(s) into Strictly Rational Functions of s § Use Long Division to Normalize the Transfer Function such that the Highest Order of the Numerator is Less Than the Highest Order of the Denominator 27

X(s) Laplace Transform: Inverse Laplace Transform Long Division § Perform long division to decompose X(s) into a constant plus a purely rational function Thus: 28

X(s) Laplace Transform: Inverse Laplace Transform Matlab Polynomial Division: deconv § The Matlab command deconv can be used to perform polynomial division [Q, R] = deconv( B, A) B = Numerator polynomial coefficients A = Denominator polynomial coefficients Q = Quotient of B/A R = Remainder of B/A § deconv operates on arrays of polynomial coefficients, NOT symbolic variables 29

X(s) Laplace Transform: Inverse Laplace Transform Long Division Verification § Use Matlab to verify the polynomial long division: » » » Q polynum = [2 1 0 -2 0]; polyden = [1 7 18 20 8]; [Q, R]=deconv(polynum, polyden) = 2 R = 0 -13 -36 -42 -16 30

X(s) Laplace Transform: Inverse Laplace Transform Expand Rational Part of X(s) § The rational part of X(s) will be referred to as Xo(s) § Partial Fraction Expansion must be performed on Xo(s) Partial Fraction Expansion § Xo(s) has 3 repeated roots and one distinct root 31

X(s) Laplace Transform: Inverse Laplace Transform Evaluating Coefficient C 4 § C 4 is evaluated using the distinct pole expression as shown in the previous example 32

X(s) Laplace Transform: Inverse Laplace Transform Matlab C 4 Verification § c 4 can verified in Matlab by creating the symbolic expression Xo and evaluating for c 4 » Xo =( -13* s^3 -36*s^2 -42*s -16)/((s+1)*(s+2)^3); » c 4 = (Xo)*(s+1) c 4 = (-13*s^3 -36*s^2 -42*s-16)/(s+2)^3 » c 4=subs(c 4, s, -1) c 4 = 3 33

X(s) Laplace Transform: Inverse Laplace Transform Evaluating Coefficient C 3 § C 3 is evaluated similar to C 4 § C 3 is easily verified in Matlab » c 3 = (Xo)*((s+2)^3); » c 3 = subs(c 3, s, -2) c 3 = -28 34

X(s) Laplace Transform: Inverse Laplace Transform Repeated Pole Coefficients § To find C 2 and C 1, the following expression must be evaluated for each case ( r = 3, p 1 = -2, i = 2, 1 ) § For simplicity, let Y(s) be the expression to be differentiated 35

X(s) Laplace Transform: Inverse Laplace Transform Repeated Pole Coefficients § C 2 equals the first derivative of Y(s) § Similarly, C 1 equals the second derivative of Y(s) / 2 § Before differentiating, Y(s) can be rewritten as: 36

X(s) Laplace Transform: Inverse Laplace Transform Calculating First Derivative § Calculating First Derivative by Hand § Matlab Verification of First Derivative » Y =(Xo)*((s+2)^3); » d. Y = diff(Y); pretty(d. Y) 2 3 2 -39 s - 72 s - 42 -13 s - 36 s - 42 s - 16 --------- - -------------s + 1 2 (s + 1) 37

X(s) Laplace Transform: Inverse Laplace Transform Simplify Y’(s) § Since Y’(s) will eventually have to be calculated, it will be helpful to simplify its terms § Matlab can also be used to perform this simplification » d. Y=simplify(d. Y); pretty(d. Y) 3 2 26 s + 75 s + 72 s + 26 - ------------2 (s + 1) 38

X(s) Laplace Transform: Inverse Laplace Transform Evaluate C 2 § C 2 can now be directly evaluated from Y’(s) § Matlab Verification of C 2 » c 2 = subs(d. Y, s, -2) c 2 = 26 39

X(s) Laplace Transform: Inverse Laplace Transform Calculate Second Derivative § The second derivative of Y(s) must be calculated to find C 1 § Matlab Verification of Y’’(s) » dd. Y = diff(d. Y); pretty(dd. Y) 2 3 2 78 s + 150 s + 72 26 s + 75 s + 72 s + 26 - --------- -+ 2 ------------2 3 (s + 1) 40

X(s) Laplace Transform: Inverse Laplace Transform Calculate C 1 § The following expression can be calculated by hand § Matlab Verification » c 1 = subs( dd. Y/2 , s , -2) c 1 = -16 41

X(s) Laplace Transform: Inverse Laplace Transform Result of Expansion § The Rational Part of X(s) is expanded to: § Thus X(s) can be rewritten as: 42

X(s) Laplace Transform: Inverse Laplace Transform Matlab Partial Fraction Expansion § Vector expressions can be evaluated using residues § As of Matlab 5. 3. x, there is currently no function to directly convert a symbolic expression to a strictly rational function, the following “trick” can be performed u u Integrate the function to be expanded Differentiate the result of the integration The result of the symbolic differentiation will be expressed in strictly rational form Thus the result of the entire process is the original function expanded into strictly rational form § Remember that the integration process MUST occur first so that no constant data is lost 43

X(s) Laplace Transform: Inverse Laplace Transform Expansion Verification § By hand, X(s) was converted to a strictly rational function § This can be verified in Matlab » » num = 2*s^4 + s^3 -2*s; den = (s+1)*( (s+2)^3 ); X = diff(int( num/den )); pretty(X) 3 28 26 16 2 + ----- - ---- + ---- - ----s + 1 3 2 s + 2 (s + 2) 44

X(s) Laplace Transform: Inverse Laplace Transform Table Method Solution § The following transform pairs can be used to evaluate x(t) § The Inverse Laplace Transform can be calculated directly LT-1 45

X(s) Laplace Transform: Inverse Laplace Transform Verification Using Matlab § Of course all of our hard work can be easily done in one step by using the ilaplace command in Matlab » x = ilaplace( X ) x = 2*Dirac(t)+3*exp(-t)-14*t^2*exp(-2*t) +26*t*exp(-2*t)-16*exp(-2*t) » pretty(x) 2 2 Dirac(t) + 3 exp(-t) - 14 t exp(-2 t) + 26 t exp(-2 t) - 16 exp(-2 t) 46

X(s) Laplace Transform: Inverse Laplace Transform Summary § Direct calculation of Inverse Laplace Transform is difficult § Practically, the Inverse Laplace Transform of a rational function is calculated using a table look-up method § Use long division and partial fraction expansion to put X(s) in strictly rational form § Two general types of poles: distinct and repeated § Matlab can be used to verify each step by hand or quickly perform the entire Inverse Laplace Transformation using ilaplace 47