Math Review with Matlab Fourier Analysis Fourier Series

Math Review with Matlab: Fourier Analysis Fourier Series S. Awad, Ph. D. M. Corless, M. S. E. E. D. Cinpinski E. C. E. Department University of Michigan-Dearborn

Fourier Analysis: Fourier Series n n n n n Periodic Signal Definition Fourier Series Representation of Periodic Signals Fourier Series Coefficients Orthogonal Signals Example: Full Wave Rectifier Complex Exponential Representation Example: Finding Complex Coefficients Magnitude and Phase Spectra of Fourier Series Parseval’s Theorem 2

Fourier Analysis: Fourier Series What is a Periodic Signal ? n n n A Periodic Signal is a signal that repeats itself every period The Period of a signal is the amount of time it takes for a given signal to complete one cycle. For example, the normal U. S. AC from wall outlet has a sine wave with a peak voltage of 170 V (110 Vrms) 3

Fourier Analysis: Fourier Series General Sinusoid n A general cosine wave, v(t), has the form: M = Magnitude, amplitude, maximum value = Angular Frequency in radians/sec (w=2 p. F) F = Frequency in Hz T = Period in seconds (T=1/F) t = Time in seconds = Phase Shift, angular offset in radians 4

Fourier Analysis: Fourier Series General Sinusoid Amplitude = 5 Plot in Blue: /2 Phase Shift Plot in Red: 1 Period = 1/60 sec. = 16. 67 ms. 5

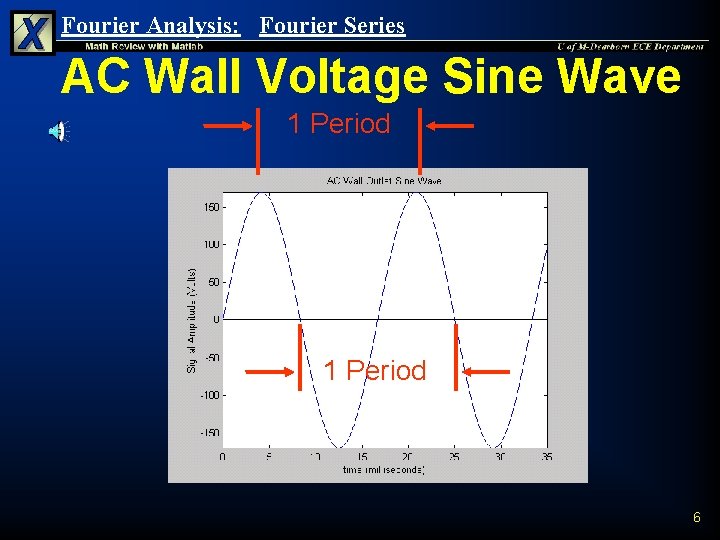
Fourier Analysis: Fourier Series AC Wall Voltage Sine Wave 1 Period 6

Fourier Analysis: Fourier Series Represent Periodic Signals n For a general periodic signal x(t) shown to the right: . . . x(t+n. T) = x(t) for all -T/2 . . . T t where n is any integer, i. e. n = 0, ± 1, ± 2, … 7

Fourier Analysis: Fourier Series Frequency of Periodic Signals n The frequency of a signal is defined as the inverse of the period and has the unit “number of cycles/sec. ” n T is the period and is the fundamental frequency. n The frequency of a US standard outlet is 1/T = 60 Hz 8

Fourier Analysis: Fourier Series What is Fourier Series ? n n Fourier Series is a technique developed by J. Fourier. This technique (studied by Fourier) allows us to represent periodic signals as a summation of sine functions of different frequency, amplitude, and phase shift. 9

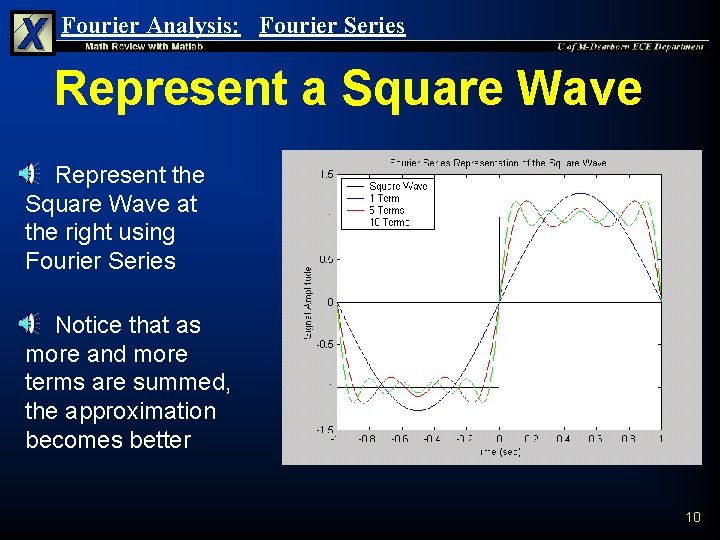
Fourier Analysis: Fourier Series Represent a Square Wave Represent the Square Wave at the right using Fourier Series n Notice that as more and more terms are summed, the approximation becomes better n 10

Fourier Analysis: Fourier Series Representation of Periodic Signals n n Any periodic function can be represented in terms of sine and cosine functions: This can also be written as: 11

Fourier Analysis: Fourier Series Coefficients n The above u a 0, an, and bn are known as the Fourier Series Coefficients. u These coefficients are calculated as follows. 12

Fourier Analysis: Fourier Series Calculating the a 0 Coefficient n n ao, the coefficient outside the summation, is known as the average value or the dc component ao is calculated as follows: 13

Fourier Analysis: Fourier Series Calculating the an and bn Coefficients n The an and bn coefficients are calculated as follows: n = 1, 2, … 14

Fourier Analysis: Fourier Series Orthogonal Signals Two periodic signals g 1(t) and g 2(t) are said to be “Orthogonal” if the integral of their product over one period is equal to zero. n 15

Fourier Analysis: Fourier Series Example: Orthogonal Signals Show that the following signals are orthogonal: n 16

Fourier Analysis: Fourier Series Orthogonal Signals 17

Fourier Analysis: Fourier Series Example: Full Wave Rectifier n Consider the output of a full-wave rectifier: x(t) y(t)=|sin( ot)| y=|x| T t y x t T/2 one period n Note that the rectified wave has a period equal to one-half of the source wave period. 18

Fourier Analysis: Fourier Series Function Characteristics n The period of y(t) = T/2 and the fundamental frequency of y(t) is 2 wo (rad/sec). n Now bn=0 since y(t) is an even function. n Thus, 19

Fourier Analysis: Fourier Series Finding ao 20

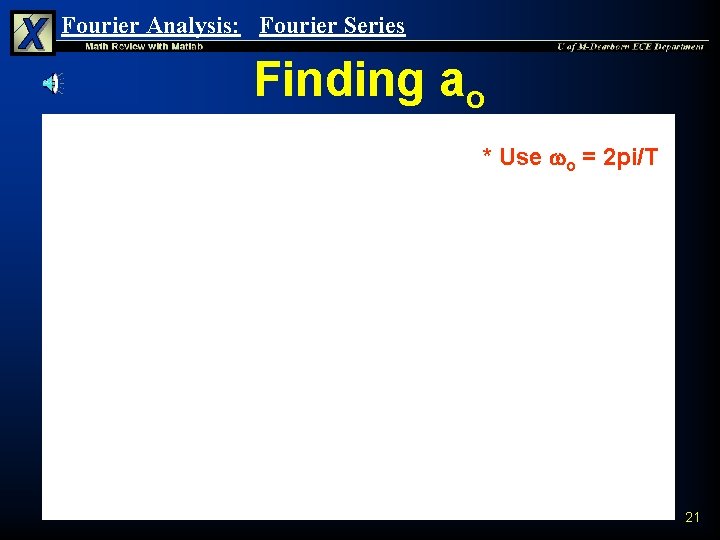
Fourier Analysis: Fourier Series Finding ao * Use o = 2 pi/T 21

Fourier Analysis: Fourier Series Finding ao 22

Fourier Analysis: Fourier Series Finding an, n = 1, 2, …. 23

Fourier Analysis: Fourier Series Solution for an, n = 1, 2, …. 24

Fourier Analysis: Fourier Series Solution for an, n = 1, 2, …. n So: n Thus: Note: We can only obtain an output signal with a nonzero average value by using a nonlinear system with our zero average value input signal n 25

Fourier Analysis: Fourier Series Euler’s Identity n n We could also say: and. . . 26

Fourier Analysis: Fourier Series Representing Sin and Cos with Complex Exponentials Add the equations: Subtract the equations: 27

Fourier Analysis: Fourier Series Complex Exponential Representation n The Sine and Cosine functions can be written in terms of complex exponentials. 28

Fourier Analysis: Fourier Series Complex Exponential Fourier Series n n From previous slides… Using the Complex Exponential representation of Sine and Cosine, the Fourier series can be written as: 29

Fourier Analysis: Fourier Series with Complex Exponentials n Noting that 1/j = -j, we can write: 30

Fourier Analysis: Fourier Series with Complex Exponentials n Make the following substitutions: 31

Fourier Analysis: Fourier Series with Complex Exponentials n The Complex Fourier series can be written as: where: n Complex cn n *Complex conjugate * n Note: if x(t) is real, c-n = cn 32

Fourier Analysis: Fourier Series Line Spectra n n Line Spectra refers the plotting of discrete coefficients corresponding to their frequencies For a periodic signal x(t), cn, n = 0, ± 1, ± 2, … are uniquely determined from x(t). The set cn uniquely determines x(t) Because cn appears only at discrete frequencies, n(wo), n = 0, ± 1, ± 2, … the set cn is called the discrete frequency spectrum or line spectrum of x(t). 33

Fourier Analysis: Fourier Series Line Spectra n n The Cn coefficients are in general complex. The standard practice is to make 2 2 D plots. u Plot 1: Magnitude of Coefficient vs. frequency u Plot 2: Phase of Coefficient vs. frequency 34

Fourier Analysis: Fourier Series Magnitude of Cn n Recall that the magnitude for a complex number a+jb is calculated as follows: 35

Fourier Analysis: Fourier Series Phase of Cn Recall that the phase for a complex number a+jb depends on the quadrant that the angle lies in. n Angle(a+jb) = Quadrant 1: Quadrant 2: Quadrant 3: Quadrant 4: 36

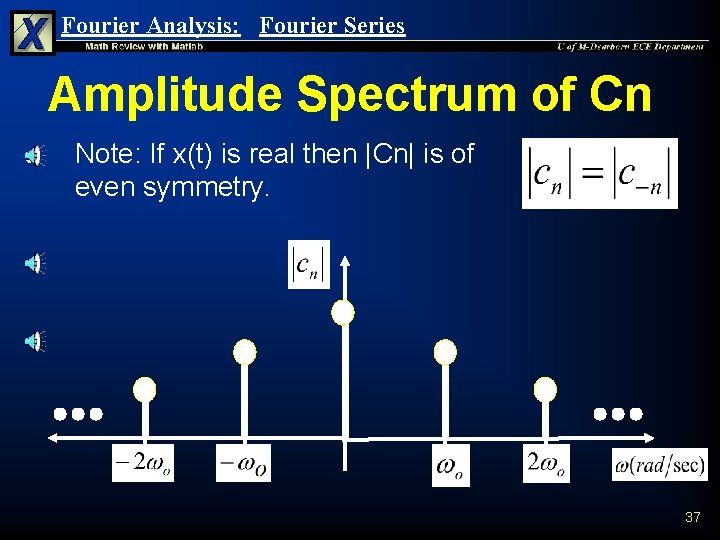
Fourier Analysis: Fourier Series Amplitude Spectrum of Cn Ü Note: If x(t) is real then |Cn| is of even symmetry. 37

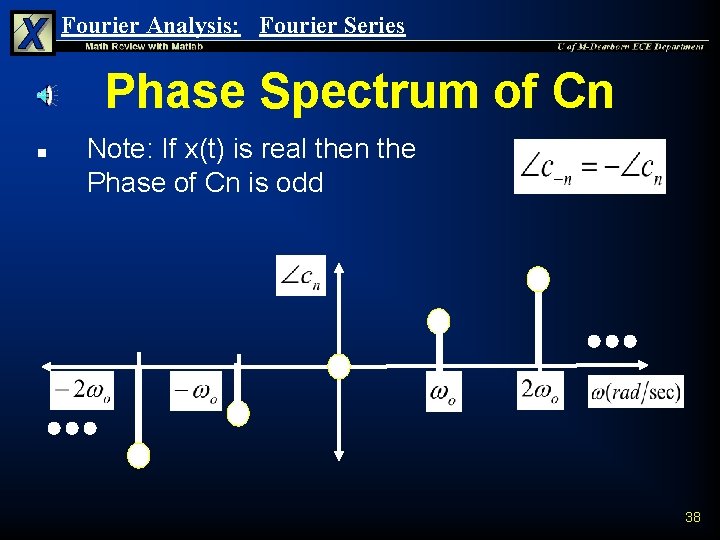
Fourier Analysis: Fourier Series Phase Spectrum of Cn n Note: If x(t) is real then the Phase of Cn is odd 38

Fourier Analysis: Fourier Series Example: Finding Complex Coefficients x(t) 1 -2. 5 -2 -1. 5 -1 -0. 5 n 0 0. 5 1 1. 5 2 2. 5 t Consider the periodic signal x(t) with period T = 2 sec. Thus: 39

Fourier Analysis: Fourier Series Finding Co(avg) The area under x(t) from -1 to -. 5 and from. 5 to 1 is zero. 0 0 Co(avg) = 0. 5 40

Fourier Analysis: Fourier Series Calculating Cn 41

Fourier Analysis: Fourier Series Factor Evaluation n Now it can be shown that: u n sin(np/2) = 0 for n = ± 2, ± 4, … Cn = 0 F sin(2 p/2) = sin(p) = 0 F sin(-4 p/2) = sin(-2 p) = 0 F etc. It can be also be shown that: sin(np/2) = -1 for n = 3, 7, 11, … u sin(np/2) = 1 for n = 1, 5, 9, … F sin(3 p/2) = -1 F sin(-7 p/2) = 1 F etc. u 42

Fourier Analysis: Fourier Series Factor Evaluation Recall: Co(avg) = 0. 5 43

Fourier Analysis: Fourier Series Summary of Results n n Note: Cn=p if Cn is negative Therefore: and 44

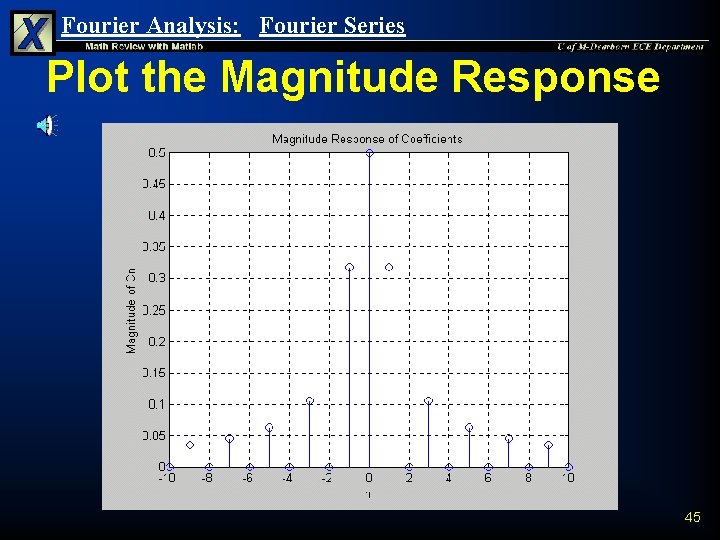
Fourier Analysis: Fourier Series Plot the Magnitude Response 45

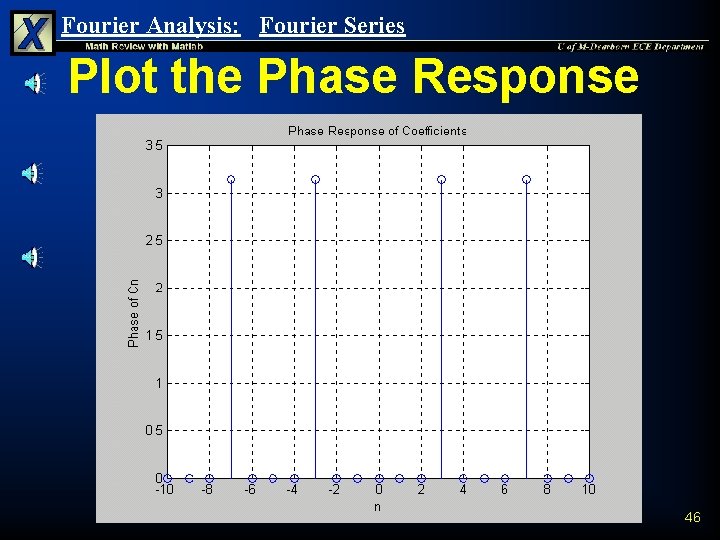
Fourier Analysis: Fourier Series Plot the Phase Response 46

Fourier Analysis: Fourier Series What is Parseval’s Theorem ? n n Parseval’s Theorem states that the average power of a periodic signal x(t) is equal to the sum of the squared amplitudes of all the harmonic components of the signal x(t). This theorem is excellent for determining the power contribution of each harmonic in terms of its coefficients 47

Fourier Analysis: Fourier Series Parseval’s Theorem n Average power of x(t) is calculated from the time or frequency domain by: Time Domain: n Frequency Domain: n 48