Math Review with Matlab Differential Equations First Order

Math Review with Matlab: Differential Equations First Order Constant Coefficient Linear Differential Equations S. Awad, Ph. D. M. Corless, M. S. E. E. E. C. E. Department University of Michigan-Dearborn

Differential Equations: First Order Systems First Order Constant Coefficient Linear Differential Equations n n First Order Differential Equations General Solution of a First Order Constant Coefficient Differential Equation n Electrical Applications n RC Application Example 2

Differential Equations: First Order Systems First Order D. E. n n A General First Order Linear Constant Coefficient Differential Equation of x(t) has the form: Where a is a constant and the function f(t) is given 3

Differential Equations: First Order Systems Properties n A General First Order Linear Constant Coefficient DE of x(t) has the properties: n The DE is a linear combination of x(t) and its derivative are multiplied by constants n There are no cross products n In general the coefficient of dx/dt is normalized to 1 n 4

Differential Equations: First Order Systems Fundamental Theorem n A fundamental theorem of differential equations states that given a differential equation of the form below where x(t)=xp(t) is any solution to: SOLUTION n and x(t)=xc(t) is any solution to the homogenous equation SOLUTION n Then x(t) = xp(t)+xc(t) is also a solution to the original DE SOLUTION 5

Differential Equations: First Order Systems f(t) = Constant Solution n If f(t) = b (some constant) the general solution to the differential equation consists of two parts that are obtained by solving the two equations: xp(t) = Particular Integral Solution xc(t) = Complementary Solution 6

Differential Equations: First Order Systems Particular Integral Solution n n Since the right-hand side is a constant, it is reasonable to assume that xp(t) must also be a constant Substituting yields: 7

Differential Equations: First Order Systems Complementary Solution n To solve for xc(t) rearrange terms n Which is equivalent to: n Taking the exponential of both sides: n Integrating both sides: n Resulting in: 8

Differential Equations: First Order Systems First Order Solution Summary n A General First-Order Constant Coefficient Differential Equation of the form: a and b are constants n Has a General Solution of the form K 1 and K 2 are constants 9

Differential Equations: First Order Systems Particular and Complementary Solutions Particular Integral Solution Complementary Solution 10

Differential Equations: First Order Systems Determining K 1 and K 2 n In certain applications it may be possible to directly determine the constants K 1 and K 2 n The first relationship can be seen by evaluating for t=0 n The second by taking the limit as t approaches infinity 11

Differential Equations: First Order Systems Solution Summary n By rearranging terms, we see that given particular conditions, the solution to: a and b are constants n Takes the form: 12

Differential Equations: First Order Systems Electrical Applications n n Basic electrical elements such as resistors (R), capacitors (C), and inductors (L) are defined by their voltage and current relationships A Resistor has a linear relationship between voltage and current governed by Ohm’s Law + - 13

Differential Equations: First Order Systems Capacitors and Inductors n n n A first-order differential equation is used to describe electrical circuits containing a single memory storage elements like a capacitors or inductor The current and voltage relationship for a capacitor C is given by: The current and voltage relationship for an inductor L is given by: 14

Differential Equations: First Order Systems RC Application Example: For the circuit below, determine an equation for the voltage across the capacitor for t>0. Assume that the capacitor is initially discharged and the switch closes at time t=0 15

Differential Equations: First Order Systems Plan of Attack n n n Write a first-order differential equation for the circuit for time t>0 The solution will be of the form K 1+K 2 e-at These constants can be found by: a u Determining vc(0) u Determining vc(¥) u Determining n Finally graph the resulting vc(t) 16

Differential Equations: First Order Systems Equation for t > 0 n n n Kirchhoff’s Voltage Law (KVL) states that the sum of the voltages around a closed loop must equal zero Ohm’s Law states that the voltage across a resistor is directly proportional to the current through it, V=IR Use KVL and Ohm’s Law to write an equation describing the circuit after the switch closes 17

Differential Equations: First Order Systems Differential Equation n Since we want to solve for vc(t), write the differential equation for the circuit in terms of vc(t) Replace i = Cdv/dt for capacitor current voltage relationship Rearrange terms to put DE in Standard Form 18

Differential Equations: First Order Systems General Solution n The solution will now take the standard form: n a can be directly determined n K 1 and K 2 depend on vc(0) and vc(¥) 19

Differential Equations: First Order Systems Initial Condition n n A physical property of a capacitor is that voltage cannot change instantaneously across it Therefore voltage is a continuous function of time and the limit as t approaches 0 from the right vc(0 -) is the same as t approaching from the left vc(0+) Before the switch closes, the capacitor was initially discharged, therefore: Substituting gives: 20

Differential Equations: First Order Systems Steady State Condition n n As t approaches infinity, the capacitor will fully charge to the source VDC voltage No current will flow in the circuit because there will be no potential difference across the resistor, v. R(¥) = 0 V 21

Differential Equations: First Order Systems Solve Differential Equation n Now solve for K 1 and K 2 n Replace to solve differential equation for vc(t) 22

Differential Equations: First Order Systems Time Constant n When analyzing electrical circuits the constant 1/a is called the Time Constant t K 1 = Steady State Solution n n t = Time Constant The time constant determines the rate at which the decaying exponential goes to zero Hence the time constant determines how long it takes to reach the steady state constant value of K 1 23

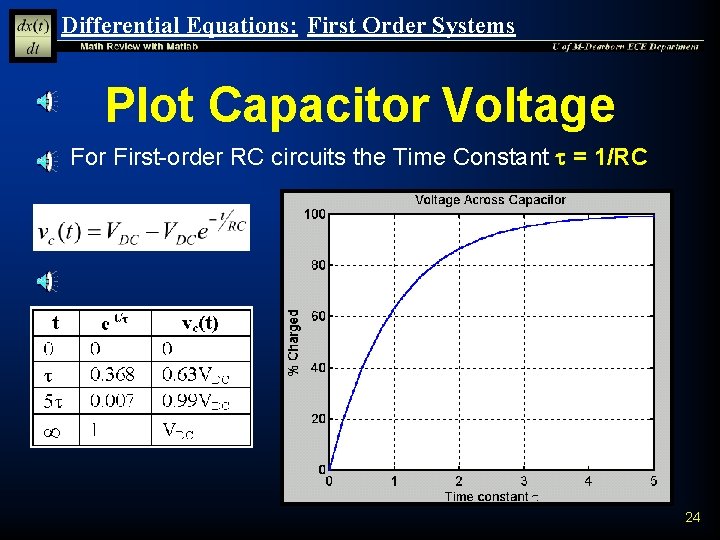
Differential Equations: First Order Systems Plot Capacitor Voltage n For First-order RC circuits the Time Constant t = 1/RC 24

Differential Equations: First Order Systems Summary n n n Discussed general form of a first order constant coefficient differential equation Proved general solution to a first order constant coefficient differential equation Applied general solution to analyze a resistor and capacitor electrical circuit 25