Math Review with Matlab Differential Equations Finding Solutions

Math Review with Matlab: Differential Equations Finding Solutions to Differential Equations S. Awad, Ph. D. M. Corless, M. S. E. E. D. Cinpinski E. C. E. Department University of Michigan-Dearborn

Differential Equations: Finding Solutions to DEs Finding Solutions to Differential Equations n n n Solving a First Order Differential Equation Solving a Second Order Differential Equation Solving Simultaneous Differential Equations Solving Nonlinear Differential Equations Numerical Solution of a Differential Equation Using the ODE 45 Solver 2

Differential Equations: Finding Solutions to DEs Solving a n st 1 Order DE The Matlab command used to solve differential equations is dsolve n Consider the differential equation: n The general solution is given by: n Verify the solution using dsolve command 3

Differential Equations: Finding Solutions to DEs Solving a Differential Equation in Matlab » syms y t » ys=dsolve('Dy+2*y=12') ys = 6+exp(-2*t)*C 1 n n C 1 is a constant which is specified by way of the initial condition Dy means dy/dt and D 2 y means d 2 y/dt 2 etc 4

Differential Equations: Finding Solutions to DEs Verify Results n Verify results given y(0) = 9 » ys=dsolve('Dy+2*y=12', 'y(0)=9') ys = 6+3*exp(-2*t) 5

Differential Equations: Finding Solutions to DEs Solving a 2 nd Order DE n Find the general solution of: » syms c y » ys=dsolve('D 2 y=-c^2*y') ys = C 1*sin(c*t)+C 2*cos(c*t) 6

Differential Equations: Finding Solutions to DEs Solving Simultaneous Differential Equations Example n Syntax for solving simultaneous differential equations is: dsolve('equ 1', 'equ 2', …) n Solve the following set of differential equations: 7

Differential Equations: Finding Solutions to DEs General Solution n Given the equations: n The general solution is given by: 8

Differential Equations: Finding Solutions to DEs Matlab Verification n n Given the equations: General solution is: » syms x y t » [x, y]=dsolve('Dx=3*x+4*y', 'Dy=-4*x+3*y') x = exp(3*t)*(cos(4*t)*C 1+sin(4*t)*C 2) y = -exp(3*t)*(sin(4*t)*C 1 -cos(4*t)*C 2) 9

Differential Equations: Finding Solutions to DEs Initial Conditions n Solve the previous system with the initial conditions: » [x, y]=dsolve('Dx=3*x+4*y', 'Dy=-4*x+3*y', 'y(0)=1', 'x(0)=0') x = exp(3*t)*sin(4*t) y = exp(3*t)*cos(4*t) 10

Differential Equations: Finding Solutions to DEs Non-Linear Differential Equation Example n Solve the differential equation: n Subject to initial condition: » syms y t » y=dsolve('Dy=4 -y^2', 'y(0)=1') » y=simplify(y) y = 2*(3*exp(4*t)-1)/(1+3*exp(4*t)) 11

Differential Equations: Finding Solutions to DEs Specifying the Independent Parameter of a Differential Equation n n If another independent variable, other than t, is used, it must be introduced in the dsolve command Solve the differential equation: » y=dsolve('Dy+2*y=12', 'x') y = 6+exp(-2*x)*C 1 12

Differential Equations: Finding Solutions to DEs Numerical Solution Example n Not all non-linear differential equations have a closed form solution, but a numerical solution can be found n Solve the differential equation: n Subject to initial conditions: n n No closed form solution exists Use the ode 45 command to get a numerical solution 13

Differential Equations: Finding Solutions to DEs Rewrite Differential Equation n Rewrite in the following form 14

Differential Equations: Finding Solutions to DEs Create a New Function n Create a Matlab function evalxdot to evaluate and numerically in terms of x 1 and x 2. function xdot=evalxdot(t, x) %x=[x 1, x 2] %xdot=[dx 1/dt, dx 2/dt]; xdot=[x(2); -9*sin(x(1))]; 15

Differential Equations: Finding Solutions to DEs ODE 45 n n n ODE 45 is used to solve non-stiff differential equations [T, Y] = ODE 45('F', TSPAN, Y 0) T = Time vector Y = Output corresponding to time vector F = Function name TSPAN = Simulation duration Y 0 = Initial conditions If the left hand side [T, Y]of the output arguments is omitted, Matlab solves it and plots it 16

Differential Equations: Finding Solutions to DEs Returning t, y and dy/dt n Run the solver with the input and output arguments specified » » » [t, y]=ode 45('evalxdot', 10, [1 0]); plot(t, y) xlabel('Time (sec)'); ylabel('Amplitude'); title('Numerical Solution'); legend('Y', 'd. Y/dt') 17
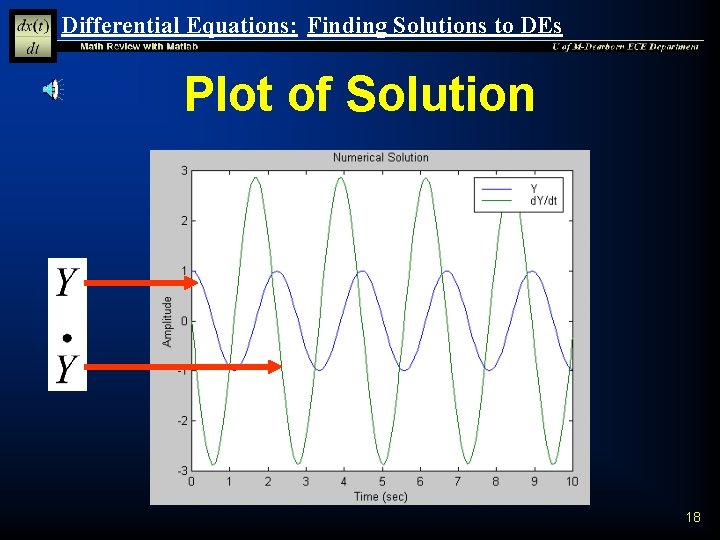
Differential Equations: Finding Solutions to DEs Plot of Solution 18

Differential Equations: Finding Solutions to DEs Omit Output Arguments n n We can run the solver again without output arguments Omitting the output arguments causes Matlab to plot the results » » » ode 45('evalxdot', 10, [1 0]); xlabel('Time (sec)'); ylabel('Amplitude'); title('Numerical Solution'); legend('Y', 'd. Y/dt') 19
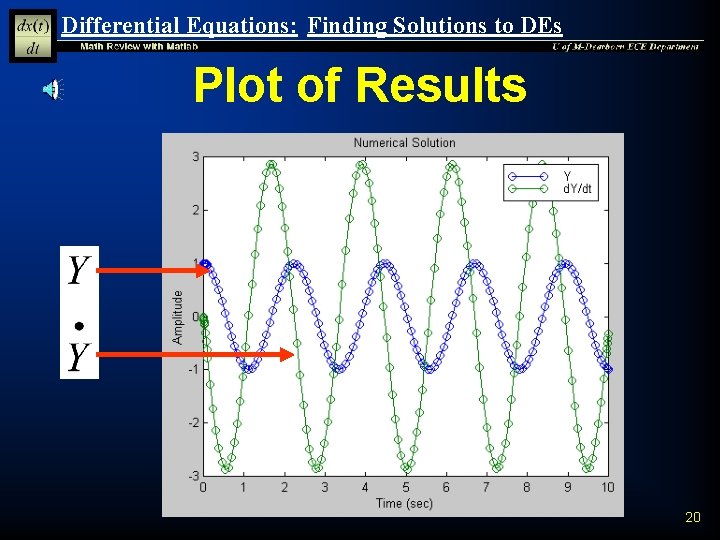
Differential Equations: Finding Solutions to DEs Plot of Results 20

Differential Equations: Finding Solutions to DEs Summary n n n The symbolic toolbox can be used to find the closed form solutions for differential equations where they exist The symbolic toolbox can be simultaneously solve a system of differential equations Other Matlab commands can be used to numerically solve systems of differential equations if closed forms do not exist 21
- Slides: 21