Math Review with Matlab Calculus Taylors Series S

Math Review with Matlab: Calculus Taylor’s Series S. Awad, Ph. D. M. Corless, M. S. E. E. D. Cinpinski E. C. E. Department University of Michigan-Dearborn

Calculus: Taylor Series Operations n Symbolic Summation n Taylor Series n Taylor Command n Taylor Series Example n Approximation and Comparison Example 2

Calculus: Taylor Series Symbolic Summation n n Find the sum of the following series s 1 and s 2 if they converges Example 1: » s 1=symsum(1/x^2, 1, inf) s 1 = Converges 1/6*pi^2 n Example 2 » num = 4*x*x-x-3 » den = x^3+2*x » s 2=symsum(num/den, 1, inf) s 2 = Diverges! inf 3

Calculus: Taylor Series Summation Examples n Example 3: » s 3=symsum(1/(x-1. 5)^2, 1, inf) s 3 = 4+1/2*pi^2 » eval(s 3) ans = 8. 9348 n Example 4: » s 4=symsum((1/x)*(-1)^(x+1), 1, inf) s 4 = log(2) » eval(s 4) ans = 0. 6931 4

Calculus: Taylor Series Finite Summation Example 5: » syms x N; » s 5=symsum((x+3)*(x+1), 1, N) s 5 = 7/6*N-11/6+3/2*(N+1)^2+1/3*(N+1)^3 » s 5=simple(s 5) s 5 = 1/6*N*(31+15*N+2*N^2) 5

Calculus: Taylor Series n n Taylor Series approximation is defined as: Mac. Laurin Series is the Taylor series approximation with a=0: 6

Calculus: Taylor Series Taylor Command n n n taylor(f) is the fifth order Mac. Laurin polynomial approximation to f taylor(f, n) is the (n -1)-st order Mac. Laurin polynomial taylor(f, n, a) is the Taylor polynomial approximation about point a with order (n -1). 7

Calculus: Taylor Series Example n Given the function: 1) Find the first 6 Taylor Series Terms (a=0) 2) Find the first 4 terms about the point a=2 » sym x; » f=log(1+x) % Matlab's Natural Log f = log(1+x) 8

Calculus: Taylor Series Terms n Find the first 6 Taylor Series Terms (a=0) » taylor(f) %Default is 5 th order ans = x-1/2*x^2+1/3*x^3 -1/4*x^4+1/5*x^5 n n Find the first 4 terms about the point a=2 Note that this is 3 rd order » taylor(f, 4, 2) ans = log(3)+1/3*x-2/3 -1/18*(x-2)^2+1/81*(x-2)^3 9

Calculus: Taylor Series Approximation and Comparison Example n Given the function: 1) Plot f(x) from -2 p to 2 p 2) Find the first 8 Taylor Series Terms (a=0) 3) Plot the approximation and compare against the original function f(x) 10

Calculus: Taylor Series Plot f(x) n n » » » The easiest way to generate a graph is to use ezplot leaves the axes unlabeled syms x f=1/(5+4*cos(x)); ezplot(f, -2*pi, 2*pi); grid on xlabel('x'); ylabel('f(x)') 11

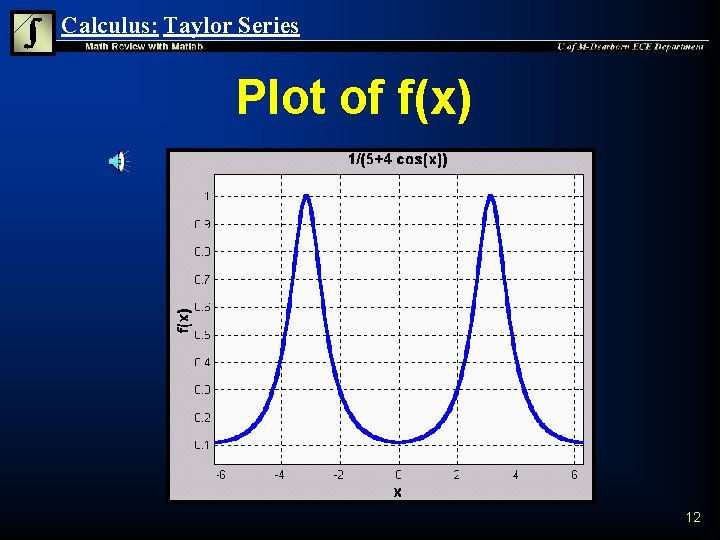
Calculus: Taylor Series Plot of f(x) 12

Calculus: Taylor Series Taylor Approximation n To find the first 8 terms of the Taylor series approximation: » ft_8=taylor(f, 8) ft_8 = 1/9+2/81*x^2+5/1458*x^4+49/131220*x^6 13

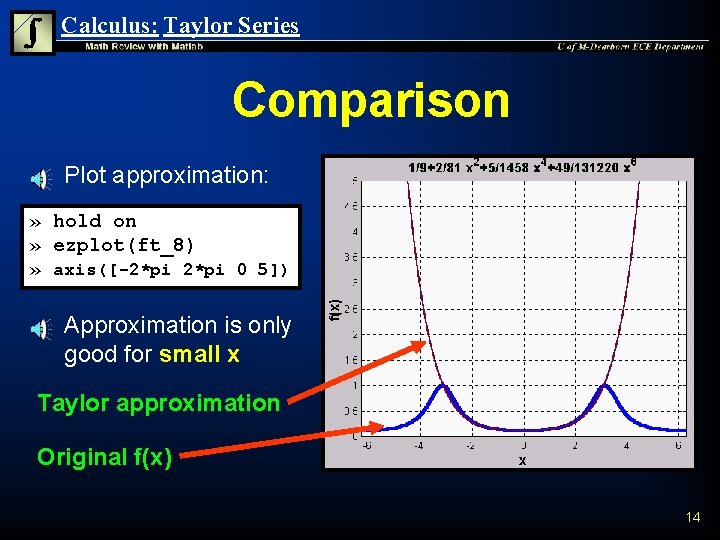
Calculus: Taylor Series Comparison n Plot approximation: » hold on » ezplot(ft_8) » axis([-2*pi 0 5]) n Approximation is only good for small x Taylor approximation Original f(x) 14

Calculus: Taylor Series Summary n n The symbolic toolbox can be used to analyze definite and indefinite series summations Taylor series can be used to approximate functions Mac. Laurin series is a special case of the Taylor series approximated around x=0 Increase the number of terms to increase approximation accuracy 15