Math Olympiad Strategies Make an Organized List Bulls

Math Olympiad Strategies Make an Organized List

Bull’s Eye �Three darts are thrown at the target shown below. Assume that each of the darts lands within one of the rings or within the bull’s eye. How many different point totals are possible? 3 4 9

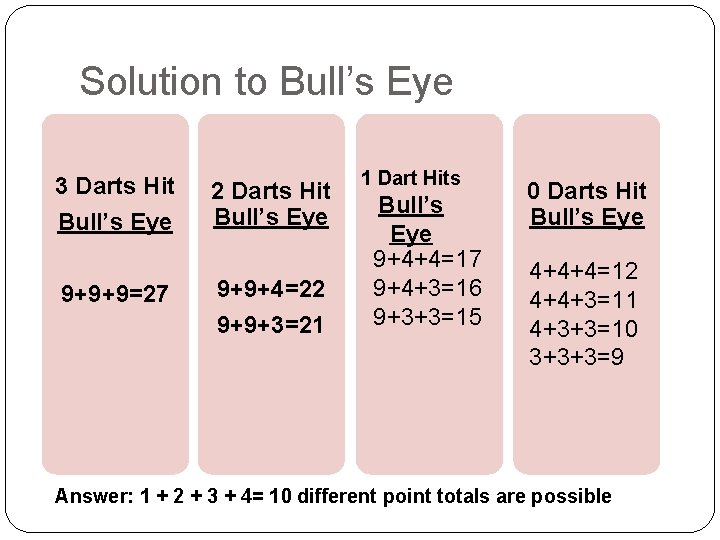
Solution to Bull’s Eye 3 Darts Hit Bull’s Eye 9+9+9=27 2 Darts Hit Bull’s Eye 9+9+4=22 9+9+3=21 1 Dart Hits Bull’s Eye 9+4+4=17 9+4+3=16 9+3+3=15 0 Darts Hit Bull’s Eye 4+4+4=12 4+4+3=11 4+3+3=10 3+3+3=9 Answer: 1 + 2 + 3 + 4= 10 different point totals are possible

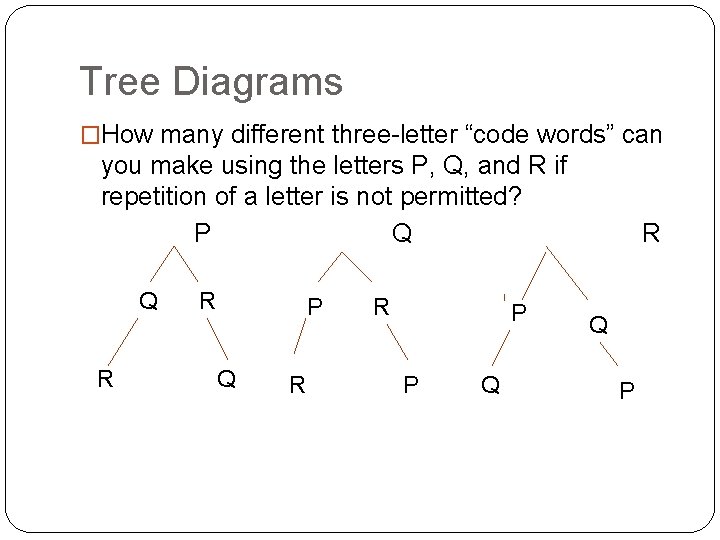
Tree Diagrams �How many different three-letter “code words” can you make using the letters P, Q, and R if repetition of a letter is not permitted? P Q Q R R P P Q R Q P

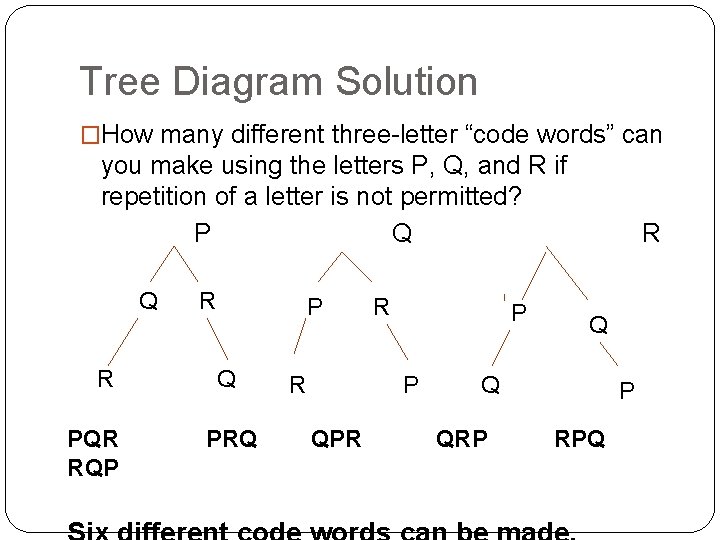
Tree Diagram Solution �How many different three-letter “code words” can you make using the letters P, Q, and R if repetition of a letter is not permitted? P Q Q R PQR RQP R P Q PRQ R R P P QPR R Q Q QRP P RPQ

Making an Organized List Homework NAME____________ Due: __________ 1. Suppose that the three regions of a target, like the example, are assigned point values of 3, 5, and 7. How many different point totals are possible if three darts are thrown and each lands somewhere on this target? 3 5 7 2. Suppose that four darts are thrown at the target described in problem 1. How many different point totals are possible if each lands on this target? 3. How many different three-letter code words can you make using the letters P, Q, and R if repetition of the letters is permitted? 4. Ken has a white shirt, a tan shirt, a pair of brown pants, a pair of black pants, a pair of blue pants, a plaid sport coat, and a tweed sport coat. How many different three-piece outfits can he make if each outfit consists of one shirt, one pair of pants, and one coat? (Hint: combinations use multiplication)

Making an Organized List Homework P. 2 5. A domino has two square spaces on its face. Each of the two square spaces is marked with 1, 2, 3, 4, 5, or 6 dots, or it is left blank. A complete set of dominoes consists of one domino for each of the possible combinations of these markings. How many dominoes are in a complet set? (Do you remember Gauss? n(n+1)/2) 6. Some antique domino sets have each of the two square faces of a domino marked with 1, 2, 3, 4, 5, 6, 7, 8, 9 dots, or left blank. How many dominoes are in a complete set of this type?