MATH II UNIT 4 Standards Functions and Their

MATH II UNIT 4

Standards: � � �

Functions and Their Inverses EQ: What are the characteristics of functions and their inverses?

Relation: � Relation � EX: – a set of ordered pairs (or graph). { (0, 1) (-5, 3) ( ½ , 23) (. 4, π) } or � Domain – x-values � Range – y-values

Functions: � Function – a relation where every x-value is paired with exactly one y-value. (No x-values can repeat) � Vertical-line-test – If a vertical line intersects the relation's graph in more than one place, then the relation is a NOT a function. Yes! No!

Inverse of a Relation: � Inverse of a Relation – when a relation is taken and all the x-values and y-values have been switched. EX: relation: {(4, 10) (8, -2) (3, 5) (18, ½ )} inverse of the relation: {(10, 4) (8, -2) (5, 3) ( ½, 18)} � The x and y coordinates have been switched.

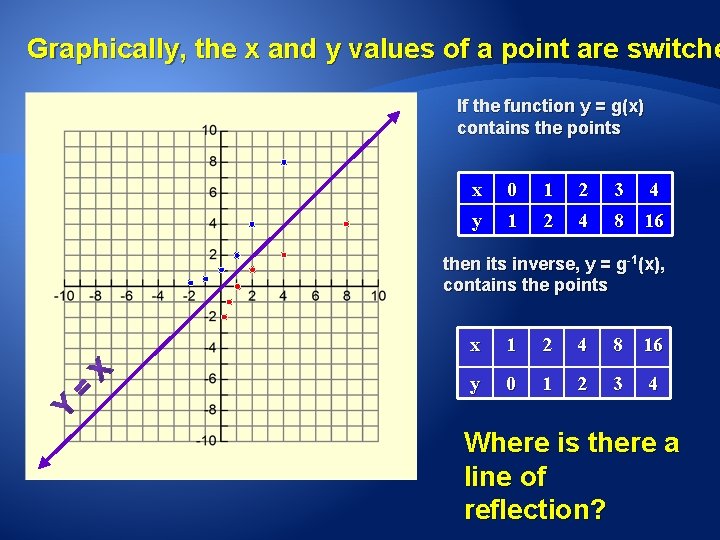
Graphically, the x and y values of a point are switche If the function y = g(x) contains the points x 0 1 2 3 4 y 1 2 4 8 16 then its inverse, y = g-1(x), contains the points x 1 2 4 8 16 y 0 1 2 3 4 Where is there a line of reflection?

The inverse of a relation is always a relation, but the inverse of a function is not always a function.

Inverse Function: � Inverse Function – � The x and y-values have been switched and the resulting relation is a function. � Both the function and the inverse function are graphed and are symmetric over the y = x line. Function Notation - f -1(x) (looks like f is raised to negative one, but is inverse notation) � Inverse

One-to-One: � When a relation is a function and its inverse is a function, then the original function is said to be one-to-one. � This means …every x-value is paired with exactly one y-value AND every y-value is paired with exactly one x-value. � Horizontal-line-test - If a horizontal line intersects the function’s graph in more than one place, then the function is NOT one-to-one. �(which means its inverse is not a function)

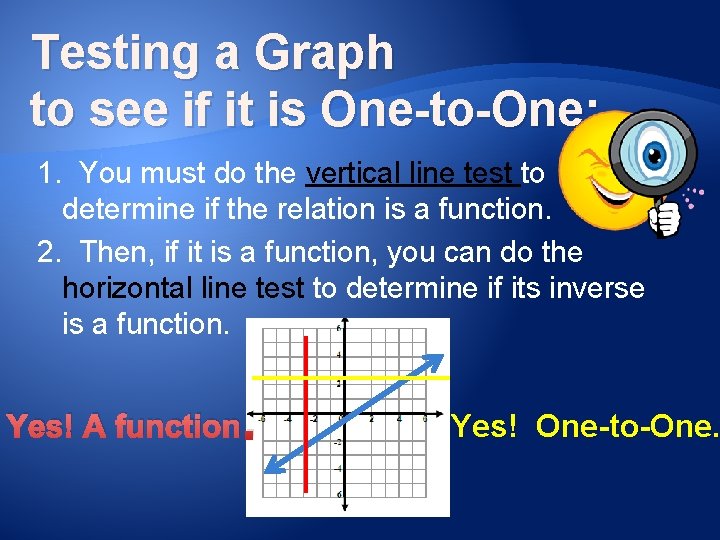
Testing a Graph to see if it is One-to-One: 1. You must do the vertical line test to determine if the relation is a function. 2. Then, if it is a function, you can do the horizontal line test to determine if its inverse is a function. Yes! A function . Yes! One-to-One.

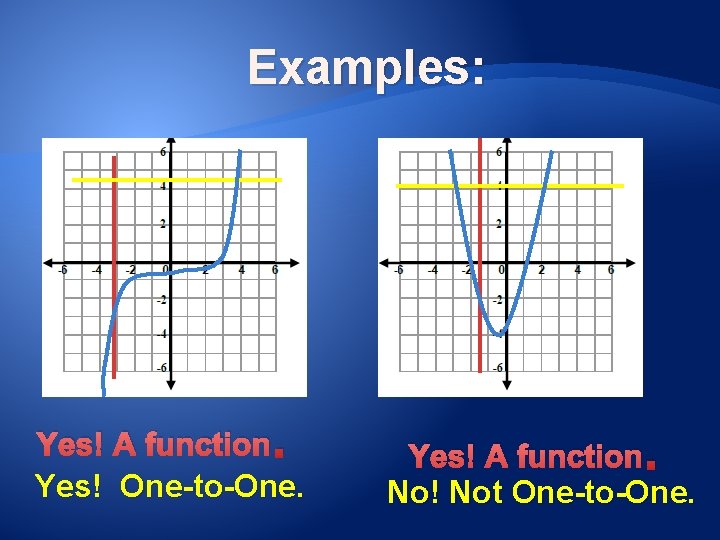
Examples: . Yes! A function Yes! One-to-One. . Yes! A function No! Not One-to-One.

Functions that are One-to. One: � All “sloping” linear functions are one-to-one. � All cubing functions are one-to-one. � Squaring functions (parabolas) are NOT oneto-one. � Absolute Value functions are NOT one-to-one (for same reason as parabola). � Square Root functions can be one-to-one, but the inverse has to have a restricted domain. . .

What does an inverse do?

Functions Imagine functions are like the dye you use to color eggs. The white egg is put in the function blue dye and the result is a blue egg.

Inverse Functions The Inverse Function “undoes” what the function does. The Inverse Function of the BLUE dye is bleach. The Bleach will “undye” the blue egg and make it white.

Inverses to Linear Functions

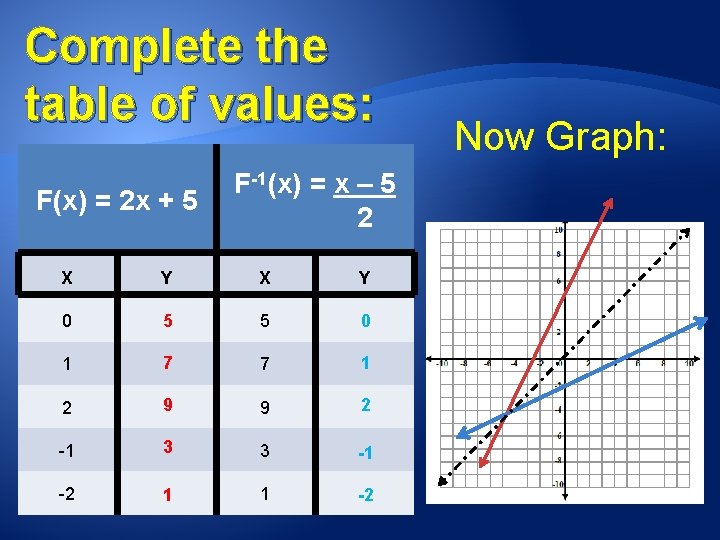
In the same way, the inverse of a given function will “undo” what the original function did. 1. Look at the function F(x) and go through the order of operations as if you were replacing x with a value. 2. Now look at the inverse function F-1(x) and go through its order of operations. F(x) = 2 x + 5 1. Multiply by 2. 2. Add 5. F-1(x) = x – 5 2 1. Subtract 5. 2. Divide by 2.

Complete the table of values: F(x) = 2 x + 5 F-1(x) = x – 5 2 X Y 0 5 5 0 1 7 7 1 2 9 9 2 -1 3 3 -1 -2 1 1 -2 Now Graph:

Steps to Finding the Inverse to a Function: � 1. Replace f(x) with y. � 2. Switch the x and y. � 3. Solve the equation for y. � 4. Replace the y with f -1(x).

Examples: � Find the inverse to the functions � 1. f(x) = 3 x – 7 2. g(x) = ½ x + 10 y = 3 x – 7 x = 3 y – 7 +7 +7 x + 7 = 3 y 3 3 x+7=y 3 f -1(x) = x + 7 3 y = ½ x + 10 x = ½ y + 10 - 10 x - 10 = ½ y 2(x – 10) = 2 ( ½ )y 2 x – 20 = y g -1(x) = 2 x - 20

Inverses to Power Functions

Inverses work for more than just linear functions. Let’s take a look at the square function: x 33 33 33 f(x) x 2 f(x) = x 2 f -1(x) y 99 9 9 99 3 3 3 3 x

Power Functions: � When a function is written in the form f(x) = xn (where n > 1) it is considered a power function. � Examples of Power Functions: 1. f(x) = x 2 2. g(x) = x 3 3. h(x) = x 4 ***How do we “undo” power functions? *** 1. 2. 3.

Find the inverse to the Power functions: � 1. f(x) = x 3 + 5 y = x 3 + 5 x = y 3 + 5 x – 5 = y 3 2. g(x) = (x – 1)3 - 2 y = (x – 1)3 – 2 x = (y – 1)3 – 2 x + 2 = (y – 1)3

Composition of Functions EQ: How do I find the composition of functions?

Composition Functions: � When we substitute one function into another one, it’s a composition of functions. � It essentially lets us perform two steps in one. � Notation: � Given f(x) and g(x) � (f o g)(x) can be written f(g(x)) …which means to substitute the function g(x) into f(x) everywhere you see an x. � (g o f)(x) – can be written g(f(x))… which means to substitute the function f(x) into g(x).

Examples: � Review: � Given f(x) = 3 x + 4 and g(x) = ½ x – 5 � 1. Find f(-3) = 3(-3) + 4 = -5 � 2. Find g(4) = ½ (4) - 5 = -3 -3 � 3. Find f(g(4)) = f(-3)= -5 � 4. Find g(f(10)) = f(10) = 3(10) + 4 = 34 g(34) = ½ (34) – 5 = 12

How do I use composition of functions to verify that functions are inverses of each other? � If two functions, f(x) and g(x), are given and you need to verify that they are inverses… �You will have to show that the composition of �(f o g)(x) = x AND (g o f)(x) = x **This is because the two functions “undo” each other and what you put in for x in the original function will be undone by the inverse. Therefore, you will get x again.

Example: � Verify that f(x) = 5 x + 1 and g(x) = x – 1 are inverses 5