Math Grade 7 Power of 10 Rules Multiplying

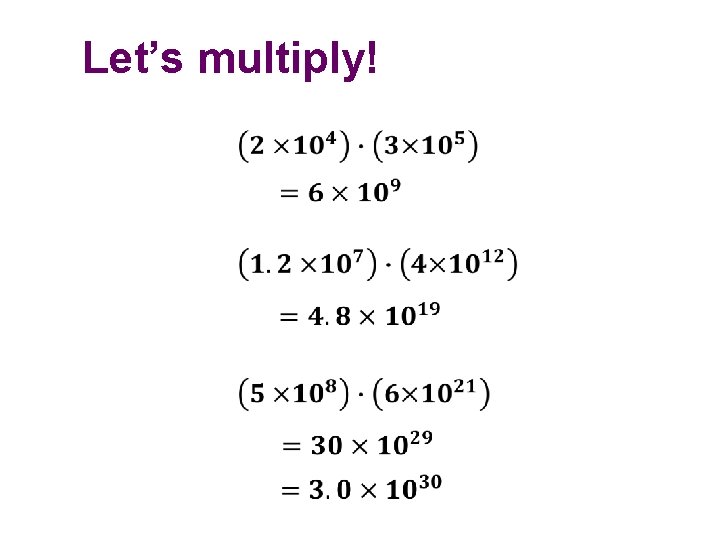
  • Slides: 21
Download presentation
Math Grade 7

Math Grade 7

Power of 10 Rules Multiplying and Dividing Scientific Notation Small Numbers Large Numbers

Power of 10 Rules Multiplying and Dividing Scientific Notation Small Numbers Large Numbers

Questions: • Is there a connection between scientific notation and the laws of exponents?

Questions: • Is there a connection between scientific notation and the laws of exponents? (What do you think? )

Let’s multiply!

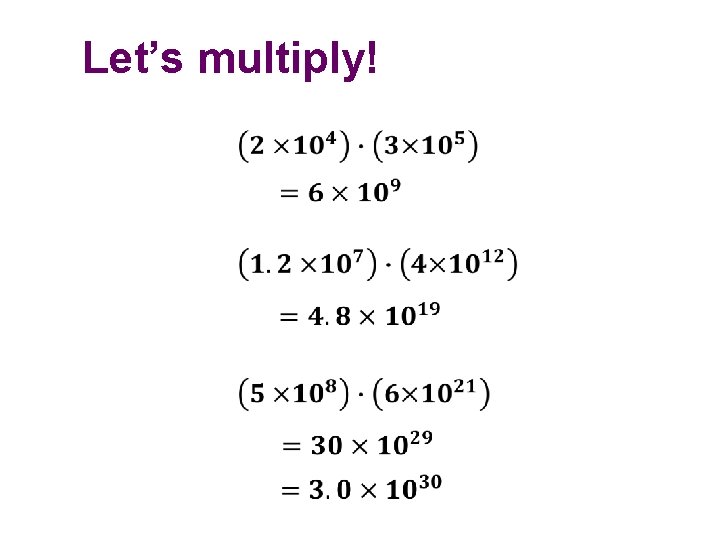
Let’s multiply!

Write the

Write the

Operations with scientific notation. Multiplying: • Multiply coefficients and then add the exponents of

Operations with scientific notation. Multiplying: • Multiply coefficients and then add the exponents of the power of 10. (7 x 102)(4 x 105) = (7 4)(102 105) = 28 x 107 • Write 28 in scientific notation. (2. 8 x 101) x 107 • Simplify. 2. 8 x 108

Practice

Practice

Consider the division of expressions with exponents, Write the for dividing scientific notations.

Consider the division of expressions with exponents, Write the for dividing scientific notations.

Let’s check your rules!

Let’s check your rules!

Operations with scientific notation. Dividing: • Divide the coefficients and then subtract the exponents

Operations with scientific notation. Dividing: • Divide the coefficients and then subtract the exponents of the power of 10. Simplify the exponents.

Practice 2 x 108 2 x 103 1 x 10 -17 3 x 10

Practice 2 x 108 2 x 103 1 x 10 -17 3 x 10 -2 3. 2 x 103 8 x 105

Operations with scientific notation. Adding: • You just add the coefficients. • Keep the

Operations with scientific notation. Adding: • You just add the coefficients. • Keep the same power of 10. (4 x 104) + (9 x 104) = (4 + 9) x 104 = 13 x 104 = 1. 3 x 105 Subtracting: • You just subtract the coefficients. • Keep the same power of 10. (8 x 104) - (2 x 104) = (8 - 2) x 104 = 6 x 104

Adding and Subtracting Scientific Notation

Adding and Subtracting Scientific Notation

• When adding or subtracting numbers in scientific notation, the exponents must be

• When adding or subtracting numbers in scientific notation, the exponents must be the same. • If the scientific notation have different exponents in the power of 10, you must move the decimal point of the coefficient to either right or left so that they will have the same exponent.

Moving the Decimal • For each move of the decimal to the right you

Moving the Decimal • For each move of the decimal to the right you have to add -1 to the exponent. • For each move of the decimal to the left you have to add +1 to the exponent.

Example 1 • Given: 2. 46 X 106 + 3. 476 X 103 •

Example 1 • Given: 2. 46 X 106 + 3. 476 X 103 • Shift decimal 3 places to the left for 103. • Move: . 003476 X 103+3 • Add: 2. 46 X 106 +. 003476 X 106 • Answer: 2. 463 X 106

Example 2 • Given: 5. 762 X 103 – 2. 65 X 10 -1

Example 2 • Given: 5. 762 X 103 – 2. 65 X 10 -1 • Shift decimal 4 places to the right for 10 -1. • Move: . 000265 X 10(-1+4) • Subtract: 5. 762 X 103 -. 000265 X 103 • Answer: 5. 762 X 103

• • (4. 12 x 106) + (3. 94 x 104) (412 x

• • (4. 12 x 106) + (3. 94 x 104) (412 x 104) + (3. 94 x 104) 412 + 3. 94 = 415. 94 x 104 • Express in proper form: 4. 15 x 106

Subtracting With Different Exponents • • (4. 23 x 103) – (9. 56 x

Subtracting With Different Exponents • • (4. 23 x 103) – (9. 56 x 102) (42. 3 x 102) – (9. 56 x 102) 42. 3 – 9. 56 = 32. 74 x 102 • Express in proper form: 3. 27 x 103

Independent Practice (4 x 103) + (3 x 102) (2 x 102) – (4

Independent Practice (4 x 103) + (3 x 102) (2 x 102) – (4 x 10) (9 x 102) + (1 x 104) (3 x 10 -6) – (5 x 10 -7) (8 x 106) + (3. 2 x 107) (9 x 1012) – (8. 1 x 10)9 (1. 32 x 10 -3) + (3. 44 x 10 -4) (2. 2 x 10 -4) – (3 x 102)