Math 8 H Wind and Current Word Problems

Math 8 H Wind and Current Word Problems Algebra 1 Glencoe Mc. Graw-Hill Jo. Ann Evans

Wind and current problems are just a variation of a type of problem you’ve worked with many times this year: =

When traveling with the current, the speed of a boat is increased by the speed of the current. An similar example is when you walk on a moving walkway at the airport. When traveling against the current, the speed of a boat is reduced by the speed of the current.

Mr. Lepire went 27 miles downstream in a boat in three hours. The return trip upstream took three times as long (nine hours). Find the rate of the boat in still water and the rate of the current. Let b = boat’s speed Let c = current’s speed Going downstream, the boat is traveling with the current. The boat’s speed will be: b + c Going upstream, the boat is traveling against the current. The boat’s speed will be: b - c

System of equations: RATE · TIME = DISTANCE with the current: against the current: ÷ all terms by 3 ÷ all terms by 9 Add the equations together. The speed of the boat is 6 mph. Find the speed of the current by substitution. Boat speed is 6 mph. Current speed is 3 mph.

Ms. Wasson took 5 hours to row 60 km downstream and 4 hours to row 40 km upstream. Find the rate of the boat in still water and the rate of the current. Let b = rate of boat in still water Let c = rate of current rate · time = distance with current: (b + c)5 = 60 b + c = 12 Divide by 5. against current: (b - c)4 = 40 b – c = 10 Divide by 4. 2 b = 22 Rowboat speed was 11 km/h and current speed was 1 km/h. b = 11

Mrs. Ashmore can swim 4 km with the current in 24 minutes. The same distance would take her 40 minutes against the current. Find the rate of the current and Mrs. Ashmore’s speed. Let s = rate swimming in still water Let c = rate of current rate · time = distance Express the times in terms of hours. with current: Simplify: against current: Simplify:

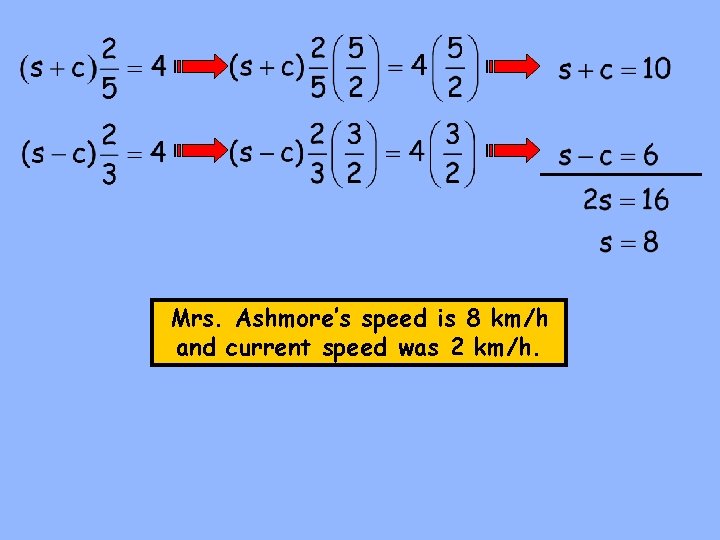
Mrs. Ashmore’s speed is 8 km/h and current speed was 2 km/h.

The rate you are traveling when you go with the wind current is a combination of the speed possible by the plane’s engine and the speed of the wind current. When you travel against the wind, the speed possible by the plane’s engine is reduced by the wind current, which is going in the opposite direction.

Flying into the wind, Mr. Wutkee flew 2800 km in 3. 5 hours. The return trip, flying with the wind, took 2. 5 hours. Find the rate of his plane in still air and the rate of the wind. Let p = rate of plane in still air Let w = rate of wind rate · time = distance (p + w)2. 5 = 2800 p + w = 1120 Divide by 2. 5. against wind: (p - w)3. 5 = 2800 p – w = 800 Divide by 3. 5. with wind: 2 p = 1920 Plane speed was 960 km/h and wind speed was 160 km/h. p = 960

The 4200 km trip from New York to San Francisco takes 6 hours flying against the wind, but only 5 hours returning. Find the speed of the plane in still air and the wind speed. Let p = rate of plane in still air Let w = rate of wind rate · time = distance with wind: (p + w)5 = 4200 p + w = 840 Divide by 5. against wind: (p - w)6 = 4200 p – w = 700 Divide by 6. 2 p = 1540 Plane speed was 770 km/h and wind speed was 70 km/h. p = 770