Math 8 H 10 1 Simplifying Radical Expressions

Math 8 H 10 -1 Simplifying Radical Expressions Algebra 1 Glencoe Mc. Graw-Hill Jo. Ann Evans

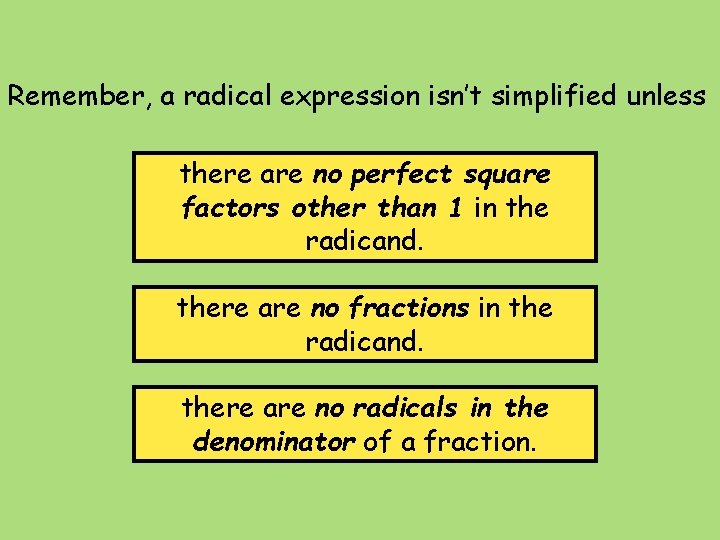
Simplifying Radical Expressions The simplest form of a radical expression is an expression that has: No perfect square factors other than 1 in the radicand. not simplified No fractions in the radicand. not simplified No radicals in the denominator of a fraction. not simplified

Product Property for Radicals: The square root of a product equals the product of the square roots of the factors. Check the validity of these statements with your calculator.

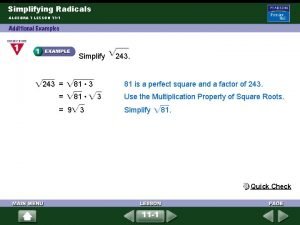
To efficiently simplify radicals using the Product Property, look for the largest perfect square factor in the radicand. Any perfect square factors? Simplify. The factors on the left worked, but took extra step. When the largest perfect square factor (16) was found, the problem was solved more efficiently.

Simplify using the Product Property of Radicals:

Multiply, then simplify the square roots. Use the product property of radicals. Are there any perfect square factors of 45? What is the positive square root of 9? Simplified answer

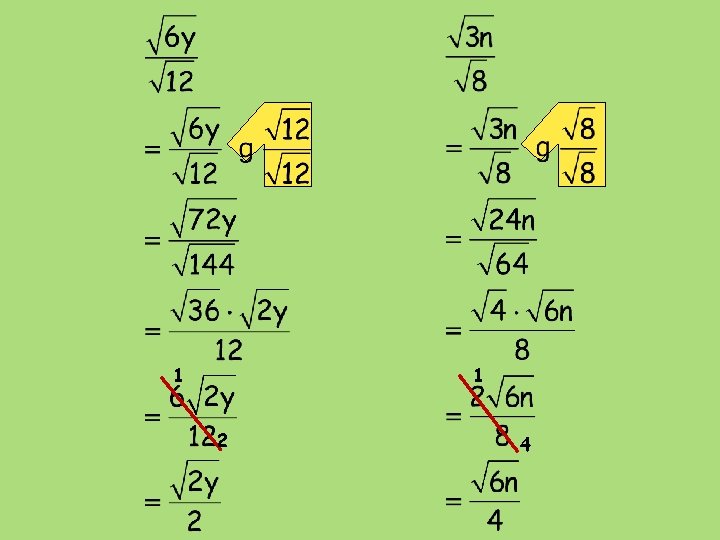
Quotient Property for Radicals: The square root of a quotient equals the quotient of the square roots of the numerator and denominator. Note: b > 0; division by zero is undefined. Zero unnnder the line is unnndefined.

If possible, write the fraction in lowest terms. Place the numerator and denominator under separate radical signs, then simplify each.

Simplify using the Quotient Property of Radicals:

Simplify using the Quotient Property of Radicals: 8 1 1 5

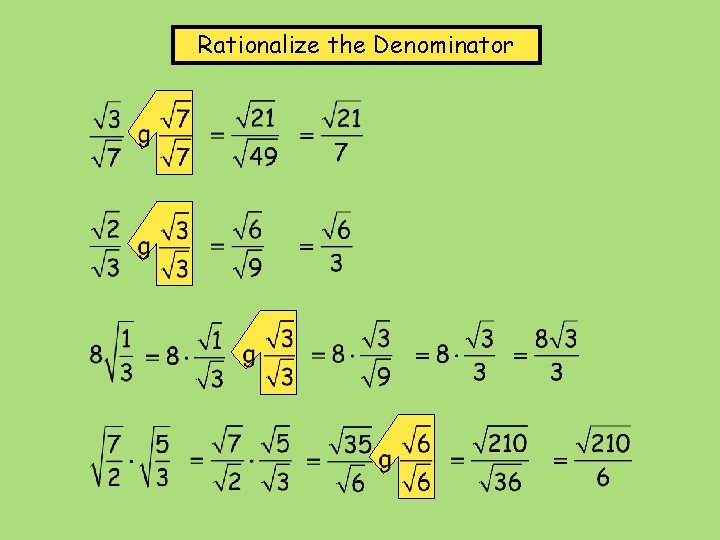
Rationalize the Denominator No radical signs may be left in the denominator. To simplify an expression that has a radical in the denominator, multiply by the BIG GIANT ONE. This is algebraically justified because it is equivalent to multiplying the original fraction by 1. Multiply the numerator and the denominator by the radical found in the denominator. Simplify the denominator. This answer is fully simplified. The denominator has been rationalized. Remember, a radical expression is not simplified if there is a radical in the denominator.

Students often wonder, “Can I cancel a number that’s under a radical and a number that’s not under a radical? ” Don’t be fooled into thinking you cancel the 2’s in this problem. The 2 you see in the numerator is the square root of 2, not 2.

Rationalize the Denominator

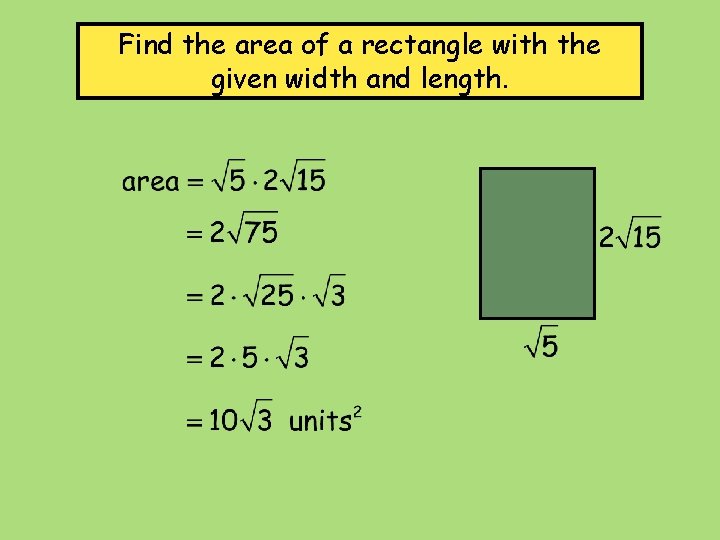
Find the area of a rectangle with the given width and length.

Find the length of the leg of the right triangle using the Pythagorean Theorem. Only the positive root will make sense in this context.

Day 2 Using the Conjugate to Rationalize a Denominator Simplify Radicals with Variables Derivation of the Quadratic Formula

Remember, a radical expression isn’t simplified unless there are no perfect square factors other than 1 in the radicand. there are no fractions in the radicand. there are no radicals in the denominator of a fraction.

Do you remember the Sum and Difference Pattern you learned when multiplying binomials? (x – 5) (x + 7) (x - 7) = x 2 + 5 x – 5 x - 25 = x 2 - 7 x + 7 x - 49 = x 2 - 25 = x 2 - 49 When the sum and difference of two terms are multiplied together, the two middle terms are opposites and will cancel out, leaving the first and last terms. The remaining terms will be squares.

Sometimes the denominator of a radical expression may have two terms. The denominator can still be rationalized using its conjugate. radical expression conjugate A radical and its conjugate are the sum and difference of the same two terms. Notice the pattern we saw earlier: The product is a rational number.

Simplify by rationalizing the denominator. No radical expression is simplified if there is a radical in the denominator. What is the conjugate of the denominator? Don’t distribute in the numerator until the denominator is rationalized.

Simplify by rationalizing the denominator. No radical expression is simplified if there is a radical in the denominator. What is the conjugate of the denominator? Don’t distribute in the numerator until the denominator is rationalized.

Simplify by rationalizing the denominator. No radical expression is simplified if there is a radical in the denominator. What is the conjugate of the denominator? Don’t distribute in the numerator until the denominator is rationalized. 4

Think of a radical symbol like a jail and the parts of the radicand as prisoners inside. Some prisoners will spend their life in the radical “jail”; others will be paroled. To be released from the radical “jail”, certain requirements must be met. Rule: A radical will only release parts that are raised to a power that matches its index. Ideas on this slide and the next from “The Complete Idiot’s Guide to Algebra” by W. Michael Kelley, 2004.

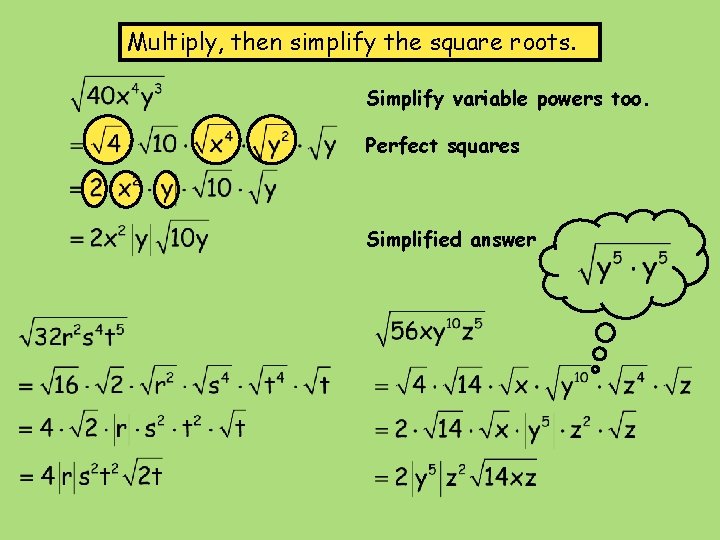
The index on a square root is 2. 42 How many parts of the radicand are raised to the 2 nd power? 16 is 42. x has an exponent of 2. Rewrite y 3 as y 2 times y. Release all parts of the radicand that have a power of 2. Why are the x and y in an absolute value symbol? An even-powered root must have a positive answer. See why on the next slide.

When finding the principal square root of an expression containing variables, be sure that the result is not negative. It may seem that the answer is… ? ? What if x has a value of -2? Substitute -2 for x in the equation. For radical expressions where the exponent of the variable inside the radical is even and the resulting simplified exponent is odd, odd you must use absolute value to ensure nonnegative results.

Multiply, then simplify the square roots. Simplify variable powers too. Perfect squares Simplified answer

1 1 2 4

Use the Quotient Property of Square Roots to Derive the Quadratic Formula! Start with standard form of a quadratic. Use the Completing the Square method. Divide each term by a. When completing the square, a must be 1. What’s next? Subtract What will complete the square? from each side. Half of , squared.

Factor as the square of a binomial. What would be a common denominator for the 2 fractions on the right side of the equation? Combine the 2 fractions over the common denominator.

Take the square root of each side. Use the Quotient Property of Square Roots. What’s the square root 4 a 2? Subtract of from both sides.

Combine the two fractions over the common denominator. There it is. . . the Quadratic Formula!