Math 4 B Systems of Differential Equations Matrix

Math 4 B Systems of Differential Equations Matrix Solutions Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

A system of 1 st order linear differential equations will have the form Here we are dealing with n-vectors and an nxn matrix A. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

The nxn system is equivalent to a single nth-order differential equation. The xi functions are simply derivatives of the xi-1 functions. Here is an example: Convert the following equation into a system of 1 st-order equations. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

The nxn system is equivalent to a single nth-order differential equation. The xi functions are simply derivatives of the xi-1 functions. Here is an example: Convert the following equation into a system of 1 st-order equations. Define variables as follows: Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

The nxn system is equivalent to a single nth-order differential equation. The xi functions are simply derivatives of the xi-1 functions. Here is an example: Convert the following equation into a system of 1 st-order equations. Define variables as follows: The original equation becomes: Now we can write down the vector equation. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

To find the solution to this system, find the eigenvalues and eigenvectors. Recall that an eigenvalue is a constant λ such that For some corresponding eigenvector. This equation will be true if the determinant of (A-λI) is 0. Prepared by Vince Zaccone This is the characteristic equation. For Campus Learning Assistance Services at UCSB

Find the roots of the characteristic equation to find the eigenvalues. After a bit of trial and error, notice that λ=-1 is an eigenvalue. This means that (λ+1) is a factor. Divide it out to get the remainder (a quadratic). Next find an eigenvector for each eigenvalue. Plug back into the matrix and row reduce: Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

For λ=-1: Any multiple of this will also be an eigenvector for λ=-1. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

For λ=-4: Any multiple of this will also be an eigenvector for λ=-4. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

For λ=3: Any multiple of this will also be an eigenvector for λ=3. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Here are the eigenvalues and their associated eigenvectors: The solution to the system is: Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Here are the eigenvalues and their associated eigenvectors: Recall the original equation was in terms of y: The solution is simply x 1(t), which is the first component of the vector solution we found The solution to the system is: Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Example: Find the solution to the given initial value problem. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Example: Find the solution to the given initial value problem. Converting to matrix form, we have: Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Example: Find the solution to the given initial value problem. Converting to matrix form, we have: We need the eigenvalues and eigenvectors for the matrix: Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Example: Find the solution to the given initial value problem. Converting to matrix form, we have: We need the eigenvalues and eigenvectors for the matrix: Eigenvector for λ=3 solves: Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Example: Find the solution to the given initial value problem. Converting to matrix form, we have: We need the eigenvalues and eigenvectors for the matrix: Eigenvector for λ=3 solves: Any multiple of this will work as an eigenvector Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Example: Find the solution to the given initial value problem. Converting to matrix form, we have: We need the eigenvalues and eigenvectors for the matrix: Eigenvector for λ=4 solves: Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Example: Find the solution to the given initial value problem. Converting to matrix form, we have: We need the eigenvalues and eigenvectors for the matrix: Eigenvector for λ=4 solves: Any multiple of this will work as an eigenvector Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

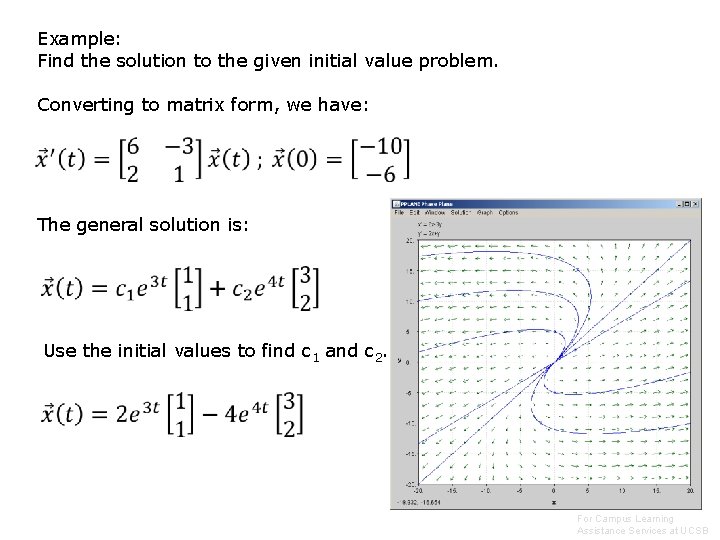
Example: Find the solution to the given initial value problem. Converting to matrix form, we have: The general solution is: Use the initial values to find c 1 and c 2. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Example: Find the solution to the given system. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Example: Find the solution to the given system. Next find eigenvectors for the eigenvalues. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

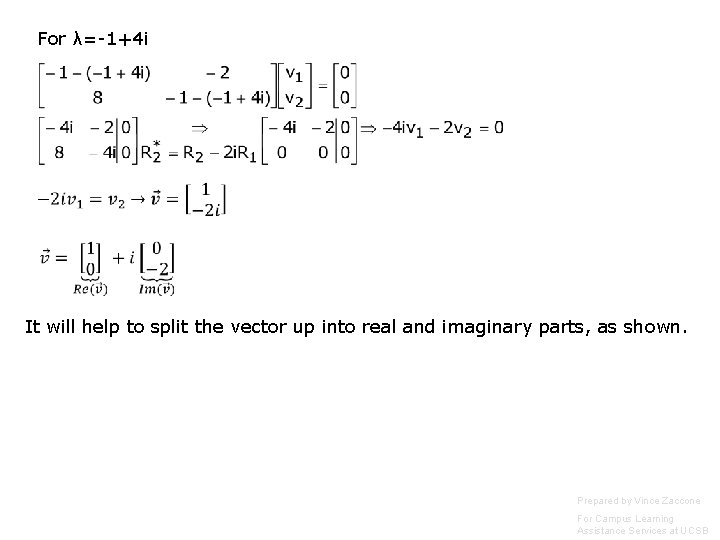
For λ=-1+4 i It will help to split the vector up into real and imaginary parts, as shown. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

For λ=-1+4 i It will help to split the vector up into real and imaginary parts, as shown. The e-vector for the other e-value will be the complex conjugate. For λ=-1 -4 i Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Now there will be a solution corresponding to each eigenvalue: Using Euler’s Formula these can be written as sines and cosines: Get real solutions by combining these: Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

The general solution is a linear combination of the real-valued solutions: The solution can be packaged more neatly through the use of the “Fundamental Matrix” of independent solutions. Each column of this matrix is one of the independent solutions X(1) and X(2). This is the fundamental matrix. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

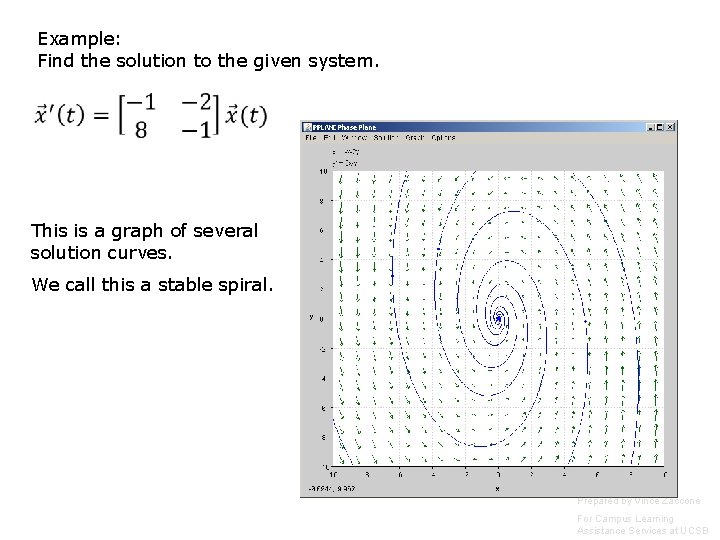
Example: Find the solution to the given system. This is a graph of several solution curves. We call this a stable spiral. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Example: Find the general solution to the given system of differential equations. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Example: Find the solution to the given system. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Example: Find the solution to the given system. First find eigenvalues and eigenvectors for the matrix. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Example: Find the solution to the given system. First find eigenvalues and eigenvectors for the matrix. We get a single eigenvector, so the geometric multiplicity is 1. This is less than the algebraic multiplicity, so we will need to find a “generalized” eigenvector to find our second solution. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Example: Find the solution to the given system. The eigenvector we have found is in the nullspace of (A-2 I). We want a generalized eigenvector in the nullspace of (A-2 I) 2. This generalized eigenvector includes the old eigenvector, plus a new constant part. We can ignore the old part and just keep the new part. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Example: Find the solution to the given system. Now we can write our general solution. Here is the template: Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB

Example: Find the solution to the given system. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB