MATH 212 Advanced Calculus 2 for Electrical Engineering

MATH 212 Advanced Calculus 2 for Electrical Engineering Advanced Calculus 2 for Nanotechnology Engineering NE 217 1 -D Finite-Element Methods with Poisson’s Equation Douglas Wilhelm Harder Department of Electrical and Computer Engineering University of Waterloo, Ontario, Canada Copyright © 2011 by Douglas Wilhelm Harder. All rights reserved.

1 -D Finite-element Methods with Poisson’s Equation Outline This topic discusses an introduction to finite-element methods – Review of Poisson’s equation – Defining a new kernel V(x) – Approximate solutions using uniform test functions 2

1 -D Finite-element Methods with Poisson’s Equation Outcomes Based Learning Objectives By the end of this laboratory, you will: – Understand how to approximate the heat-conduction/diffusion and wave equations in two and three dimensions – You will understand the differences between insulated and Dirichlet boundary conditions 3

1 -D Finite-element Methods with Poisson’s Equation The Target Equation Recall the first of Maxwell’s equations (Gauss’s equation): If we are attempting to solve for the underlying potential function, under the assumption that it is a conservative field, we have This is in the form of Poisson’s equation 4

1 -D Finite-element Methods with Poisson’s Equation The Target Equation In one dimension, this simplifies to: Define: and thus we are solving for 5

1 -D Finite-element Methods with Poisson’s Equation The Integral If , it follows that for any test function f(x) and therefore Substituting the alterative definition of V(x) into this equation, we get 6

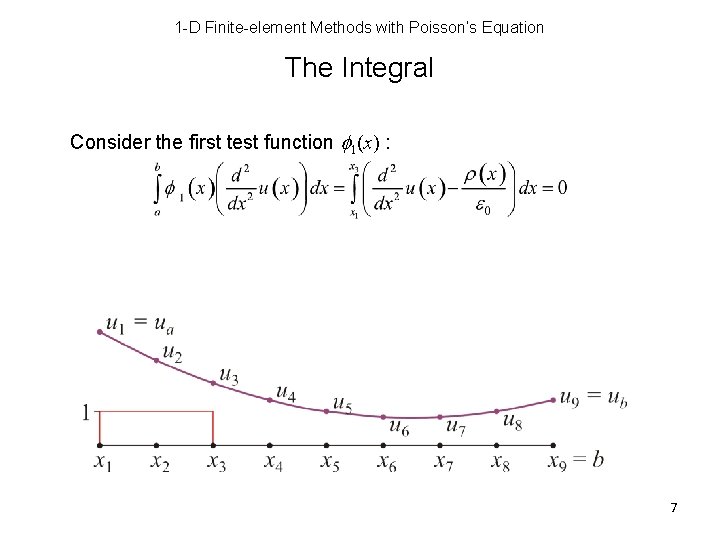
1 -D Finite-element Methods with Poisson’s Equation The Integral Consider the first test function f 1(x) : 7

1 -D Finite-element Methods with Poisson’s Equation Integration by Parts Again, take but before we apply integration by parts, expand the integral: Everything in the second integral is known: bring it to the right: 8

1 -D Finite-element Methods with Poisson’s Equation Integration by Parts The left-hand integral is no different from before, and performing integration by parts, we have 9

1 -D Finite-element Methods with Poisson’s Equation Integration by Parts First, substituting in the first test function: which yields 1 10

1 -D Finite-element Methods with Poisson’s Equation The System of Linear Equations Again, recall that we approximated the solution by unknown piecewise linear functions: where we define on 11

1 -D Finite-element Methods with Poisson’s Equation Unequally Spaced Points Recall that we approximated the left-hand integral by substituting the piecewise linear functions to get: 12

1 -D Finite-element Methods with Poisson’s Equation Integration by Parts That is, our linear equations are: This time, let’s take an actual example 13

1 -D Finite-element Methods with Poisson’s Equation Integration by Parts Consider the equation with the boundary conditions u(0) = 0 u(1) = 0 14

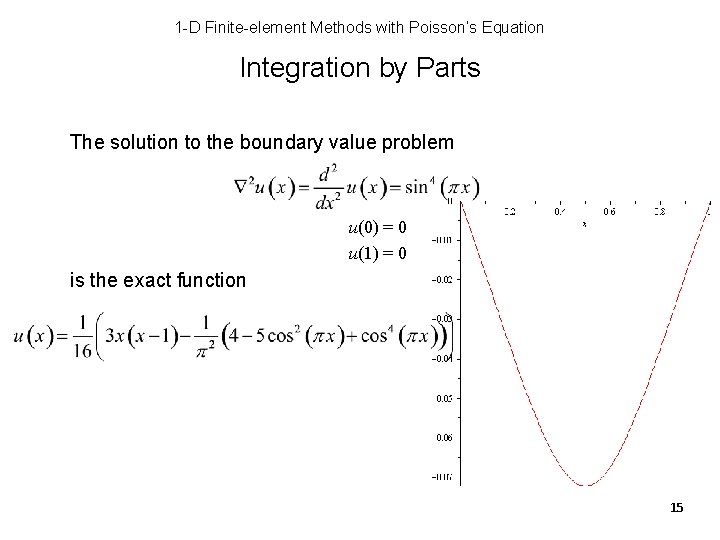
1 -D Finite-element Methods with Poisson’s Equation Integration by Parts The solution to the boundary value problem u(0) = 0 u(1) = 0 is the exact function 15

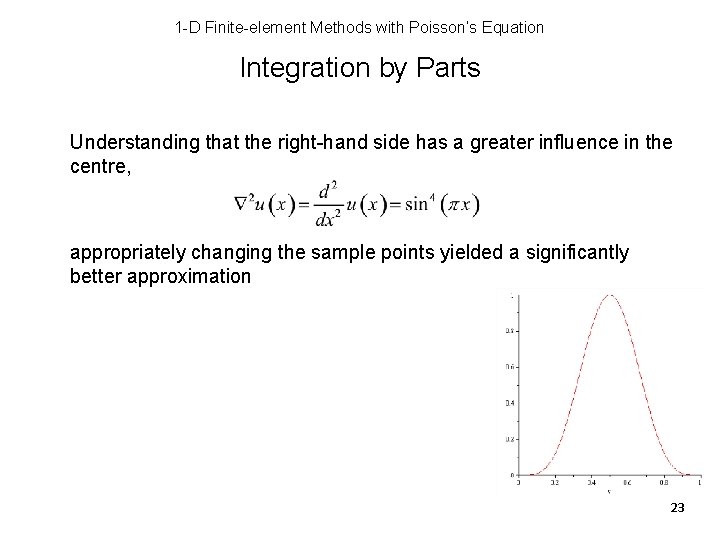
1 -D Finite-element Methods with Poisson’s Equation Integration by Parts We know in one dimension if the right-hand side is close to zero, the solution is a straight line Thus, choose 9 interior points with a focus on the centre: >> x_uneq = [0 0. 16 0. 25 0. 33 0. 41 0. 59 0. 67 0. 75 0. 84 1]; 16

1 -D Finite-element Methods with Poisson’s Equation Integration by Parts We will compare this approximation with the approximation found using 9 equally spaced interior points – The finite difference approximation >> x_eq = 0: 0. 1: 1; 17

1 -D Finite-element Methods with Poisson’s Equation The Test Functions The function to find the approximations is straight-forward: function [ v ] = uniform 1 d( x, uab, rho ) n = length( x ) - 2; idx = 1. /diff(x); M = diag( -(idx( 1: end - 1 ) + idx( 2: end )) ) +. . . diag( idx( 2: end - 1 ), -1 ) +. . . diag( idx( 2: end - 1 ), +1 ); b = zeros ( n, 1 ); int( rho, a, b ) approximates for k = 1: n b(k) = 0. 5*int( rho, x(k), x(k + 2) ); end b(1) = b(1) - idx(1)*uab(1); b(end) = b(end) - idx(end)*uab(end); v = [uab(1); M b; uab(2)]; end 18

1 -D Finite-element Methods with Poisson’s Equation The Test Functions The right-hand function of is also straight-forward: function [ u ] = rho( x ) u = sin( pi*x ). ^4; end 19

1 -D Finite-element Methods with Poisson’s Equation The Equations Thus, we can find our two approximations: >> >> >> x_eq = (0: 0. 1: 1)'; plot( x_eq, uniform 1 d( x_eq, [0, 0], @rho ), 'b+' ); hold on x_uneq = [0 0. 16 0. 25 0. 33 0. 41 0. 59 0. 67 0. 75 0. 84 1]'; plot( x_uneq, uniform 1 d( x_uneq, [0, 0], @rho ), 'rx' ); 20

1 -D Finite-element Methods with Poisson’s Equation The Equations It is difficult to see which is the better function, therefore create a function storing the actual solution (as found in Maple): function u = u(x) u = -1/16*( (cos(pi*x). ^4 - 5*cos(pi*x). ^2 + 4)/pi^2 + 3*x. *(x - 1) ); end . . 21

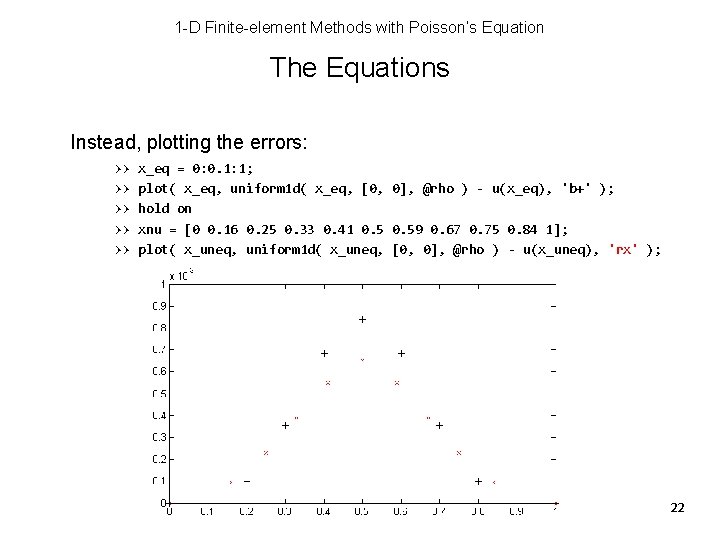
1 -D Finite-element Methods with Poisson’s Equation The Equations Instead, plotting the errors: >> >> >> x_eq = 0: 0. 1: 1; plot( x_eq, uniform 1 d( x_eq, [0, 0], @rho ) - u(x_eq), 'b+' ); hold on xnu = [0 0. 16 0. 25 0. 33 0. 41 0. 59 0. 67 0. 75 0. 84 1]; plot( x_uneq, uniform 1 d( x_uneq, [0, 0], @rho ) - u(x_uneq), 'rx' ); 22

1 -D Finite-element Methods with Poisson’s Equation Integration by Parts Understanding that the right-hand side has a greater influence in the centre, appropriately changing the sample points yielded a significantly better approximation 23

1 -D Finite-element Methods with Poisson’s Equation Summary In this topic, we have generalized Laplace’s equation to Poisson’s equation – Used the same uniform test functions – We looked at a problem for which there is an exact solution • Changing the points allowed us to get better approximations 24

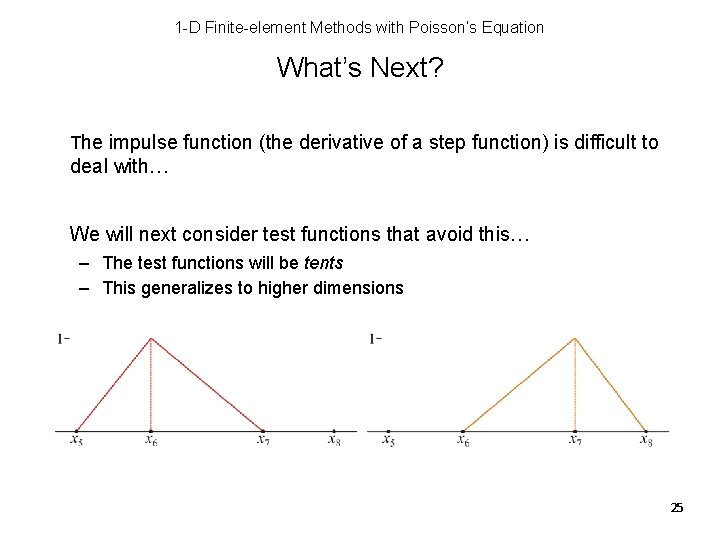
1 -D Finite-element Methods with Poisson’s Equation What’s Next? The impulse function (the derivative of a step function) is difficult to deal with… We will next consider test functions that avoid this… – The test functions will be tents – This generalizes to higher dimensions 25

1 -D Finite-element Methods with Poisson’s Equation References [1] Glyn James, Advanced Modern Engineering Mathematics, 4 th Ed. , Prentice Hall, 2011, §§ 9. 2 -3. 26

1 -D Finite-element Methods with Poisson’s Equation Usage Notes • • These slides are made publicly available on the web for anyone to use If you choose to use them, or a part thereof, for a course at another institution, I ask only three things: – that you inform me that you are using the slides, – that you acknowledge my work, and – that you alert me of any mistakes which I made or changes which you make, and allow me the option of incorporating such changes (with an acknowledgment) in my set of slides Sincerely, Douglas Wilhelm Harder, MMath dwharder@alumni. uwaterloo. ca 27