MATH 200 WEEK 2 WEDNESDAY PARAMETRIC EQUATIONS OF

MATH 200 WEEK 2 - WEDNESDAY PARAMETRIC EQUATIONS OF

MATH 200 MAIN QUESTIONS FOR TODAY ▸ How do we describe lines in space? ▸ How do we determine if two lines are parallel, intersecting, or skew? ▸ How do we figure out where lines intersection the coordinate planes?

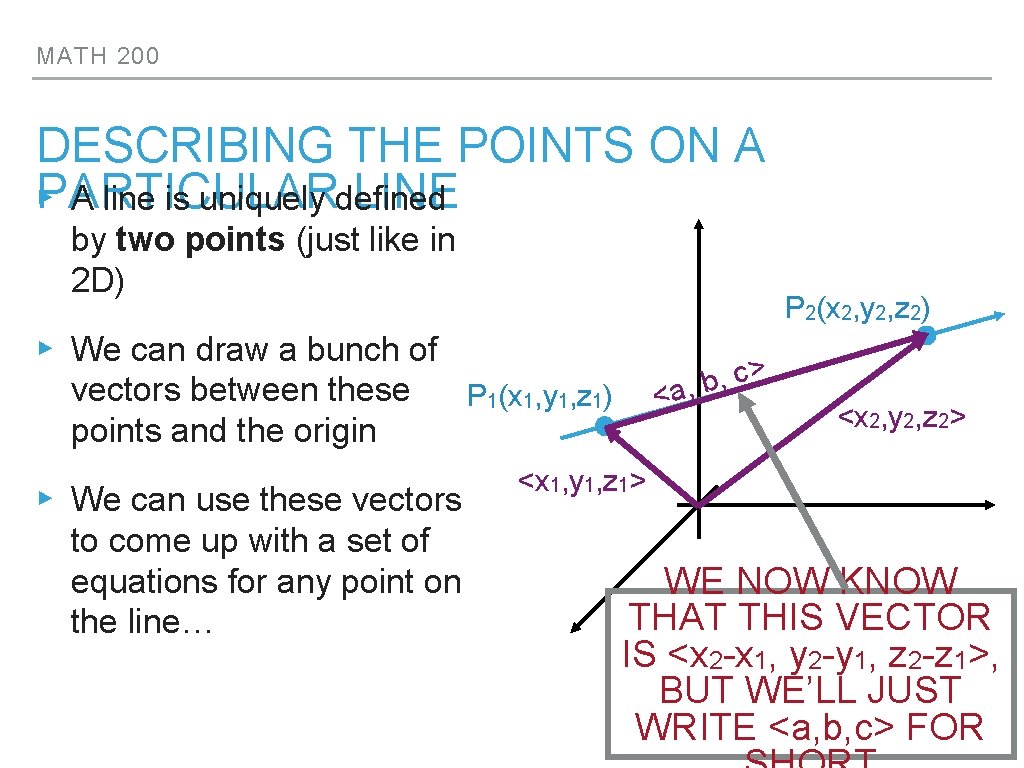
MATH 200 DESCRIBING THE POINTS ON A LINE ▸PARTICULAR A line is uniquely defined by two points (just like in 2 D) P 2(x 2, y 2, z 2) ▸ We can draw a bunch of vectors between these points and the origin ▸ We can use these vectors to come up with a set of equations for any point on the line… > c , b <a, P 1(x 1, y 1, z 1) <x 2, y 2, z 2> <x 1, y 1, z 1> WE NOW KNOW THAT THIS VECTOR IS <x 2 -x 1, y 2 -y 1, z 2 -z 1>, BUT WE’LL JUST WRITE <a, b, c> FOR

MATH 200 ▸ We want to describe an arbitrary point on the line in terms of the vectors we drew ▸ <x 1, y 1, z 1> will get us to P 1 (x, y, z) > c , b , ▸ <a, b, c> gets us from P 1 to a < t > c , b <a, <x, y, z> P 2 ▸ Scalar multiples of <a, b, c> will go back and forth along the line! <x 1, y 1, z 1>

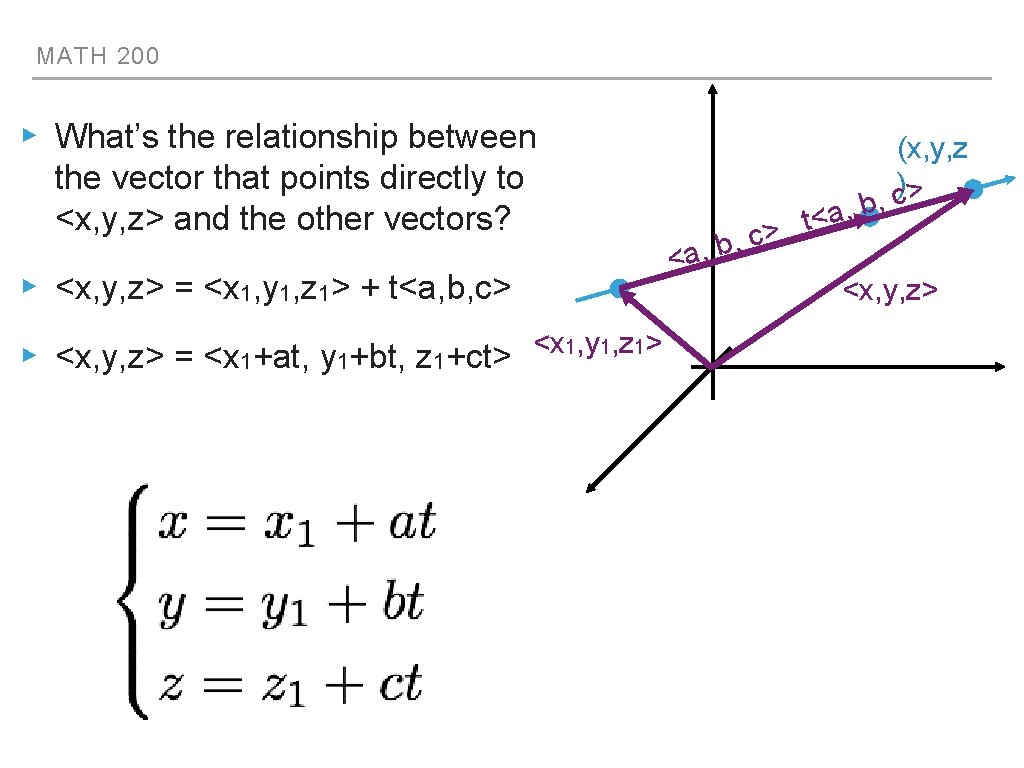
MATH 200 ▸ What’s the relationship between the vector that points directly to <x, y, z> and the other vectors? ▸ <x, y, z> = <x 1, y 1, z 1> + t<a, b, c> ▸ <x, y, z> = <x 1+at, y 1+bt, z 1+ct> <x 1, y 1, z 1> (x, y, z )> c b, a, < t > c , <a, b <x, y, z>

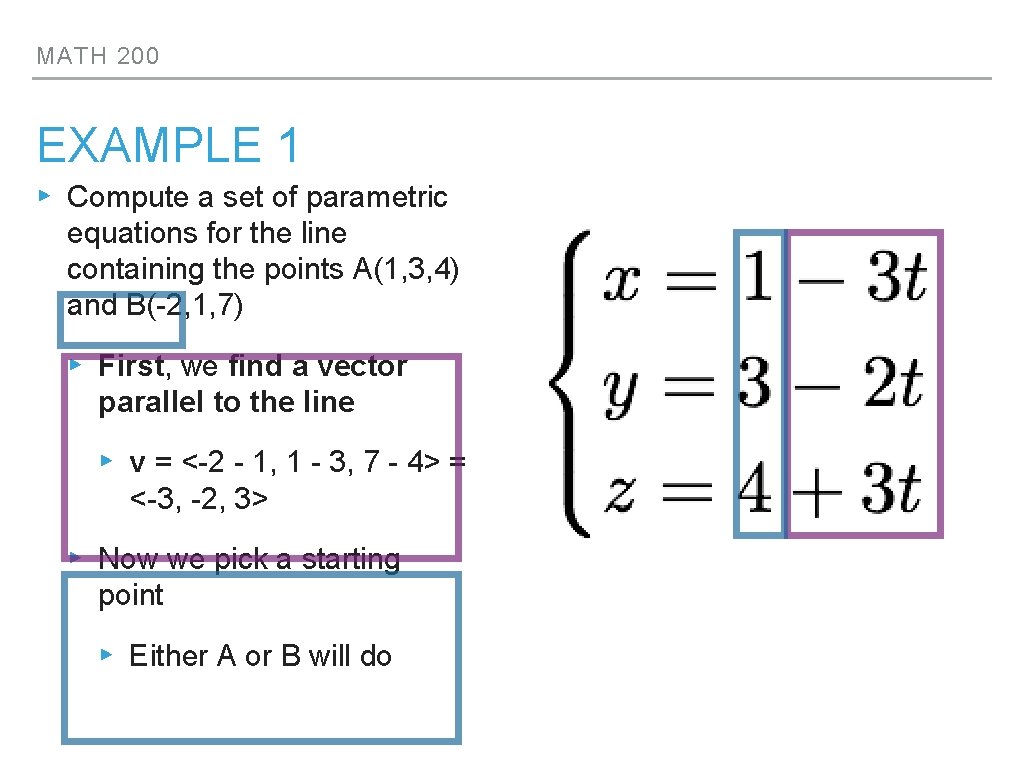
MATH 200 EXAMPLE 1 ▸ Compute a set of parametric equations for the line containing the points A(1, 3, 4) and B(-2, 1, 7) ▸ First, we find a vector parallel to the line ▸ v = <-2 - 1, 1 - 3, 7 - 4> = <-3, -2, 3> ▸ Now we pick a starting point ▸ Either A or B will do

MATH 200 YOU TRY ONE ▸ Find a set of parametric equations for the line containing the points A(4, -2, 0) and B(3, 3, -1). ▸ Find another point on the line. TO GET ANOTHER POINT ON THE LINE, WE CAN JUST PLUG IN ANOTHER “TIME” VALUE FOR t. E. G. WHEN t = -1 WE GET (5, -7, 1)

MATH 200 ANOTHER EXAMPLE ▸ Find a set of parametric equations for the line that passes through the point A(1, 4, 2) and is parallel to the xy-plane and the yz-plane. ▸ If it’s parallel to both the xy-plane and the yz-plane, then its direction vector must have x- and z-components that are zero ▸ e. g. <0, 1, 0> would work 4

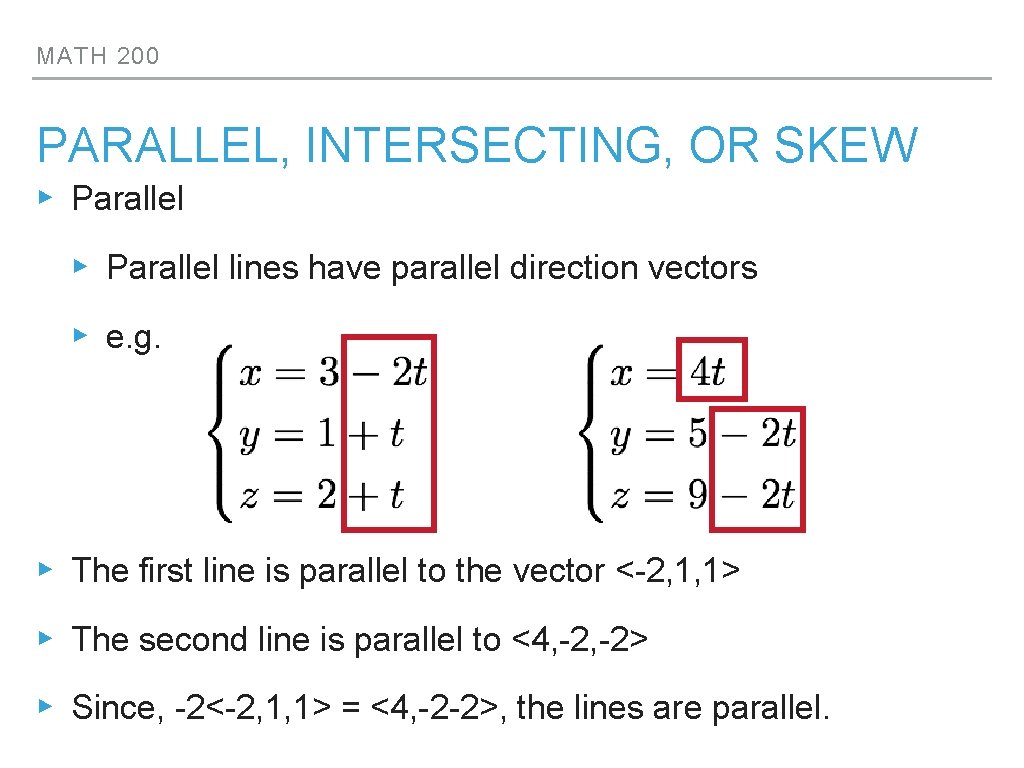
MATH 200 PARALLEL, INTERSECTING, OR SKEW ▸ Parallel lines have parallel direction vectors ▸ e. g. ▸ The first line is parallel to the vector <-2, 1, 1> ▸ The second line is parallel to <4, -2> ▸ Since, -2<-2, 1, 1> = <4, -2 -2>, the lines are parallel.

MATH 200 ▸ Skew vs intersecting ▸ Suppose we have two lines that are not parallel ▸ e. g. ▸ We know they’re not parallel because <-1, 3, -2> is not parallel to <4, -1, 1>. ▸ They may intersect, but they may pass right by one another…

EVEN IF THEY DO INTERSECT, THEY MAY PASS THROUGH THEIR COMMON POINT FOR DIFFERENT t -VALUES! RATHER THAN SETTING THE EQUATIONS EQUAL AS GIVEN, WE’LL NEED DIFFERENT LETTERS FOR THE PARAMETER IN EACH! PICK TWO EQUATIONS AND SOLVE FOR a AND b