MATH 175 NUMERICAL ANALYSIS II Lecturer Jomar Fajardo

MATH 175: NUMERICAL ANALYSIS II Lecturer: Jomar Fajardo Rabajante AY 2012 -2013 IMSP, UPLB

MODELS ONE ORDINARY DIFFERENTIAL EQUATION: • Population Dynamics (e. g. Malthusian, Verhulstian, Gompertz, Logistic with Harvesting) • Harmonic Oscillator (e. g. pendulum) • A modified normal distribution curve • The savings problem

MODELS SYSTEMS OF ODEs: • Romeo and Juliet Love Story • Conflict Models (e. g. combat models) • Interacting species Models (e. g. Lotka-Volterra predatorprey) • Compartment Models – – – Tank Mixing Problem Epidemics model Rumor model Electrical Network Aquatic Compartment Model • Chemical Kinetics • The Lorenz Equations (Example of Chaos)

The basic steps in building a model are: • Step 1: Clearly state the (intelligent) assumptions on which the model will be based. These assumptions should describe the relationships among the quantities to be studied. • Step 2: Completely describe the parameters and variables to be used in the model. • Step 3: Use the assumptions (from Step 1) to derive mathematical equations (our model) relating the parameters and variables (from Step 2). • Step 4: If applicable, verify or revise the model. http: //www. sosmath. com

RECALL • Direct and Inverse Proportionality • Joint Variation • Direct and Inverse Exponential Proportionality • Direct and Inverse Logarithmic Proportionality • Etc…

ONE ODEquation The reason DEs are so important is that often we don’t know exactly how variables are related, but we can write equations relating their derivatives (rates of change). ____________________ POPULATION DYNAMICS (Single Species): Change in Population = number of births – number of deaths + immigration – emigration

MALTHUSIAN GROWTH MODEL (Exponential Growth) Let P(t) or simply P be the population at time t. Let b be the constant intrinsic per-capita birth rate and d be the constant intrinsic per-capita death rate; r be the constant intrinsic (net) per-capita growth rate. ASSUMPTIONS: 1. The change in the population (rate of reproduction) of a community is directly proportional to the community’s current population. 2. There is no immigration and emigration. No competition.

MALTHUSIAN GROWTH MODEL (Exponential Growth) Analytic Solution: Note: Exponential Growth/Decay Model is also applicable to many problems, e. g. compoundedcontinuously interest model, and Radioactive decay

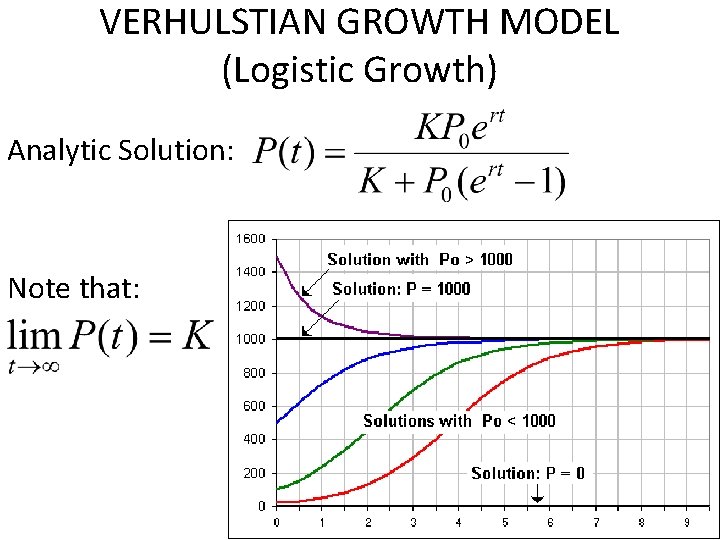
VERHULSTIAN GROWTH MODEL (Logistic Growth) ASSUMPTIONS: 1. Still no immigration and emigration. No interspecific competition. 2. The change in population is jointly proportional to the existing population and the amount of available resources. The factor 1 – P/K is close to 1 (i. e. , has no effect) when P is much smaller than K; and is close to 0 when P is close to K. (r is the constant intrinsic per-capita growth rate; K>0 is the constant carrying capacity; P(0)=P 0)

VERHULSTIAN GROWTH MODEL (Logistic Growth) Verhulst derived his logistic equation to describe the self-limiting growth of a biological population. In the equation, the early, unimpeded growth rate is modeled by the first term +r. P. Later, as the population grows, the second term, which is −r. P 2/K, becomes larger than the first as some members of the population P interfere with each other by competing (intraspecific) for some critical resource, such as food or living space.

VERHULSTIAN GROWTH MODEL (Logistic Growth) Analytic Solution: Note that:

Logistic with Harvesting Analytic solutions to this ODE are usually difficult to find. Commonly numerical and qualitative analysis are applied.

Logistic with CONSTANT Harvesting Let a be the amount of harvesting (yield) per unit time. As we increase our yield a, the recovery time increases. If then recovery time is infinite (i. e. this may drive the population to extinction).

LAWS OF PHYSICS Our discussion would not be complete without mentioning what is probably the biggest source of differential equation models – laws of physics!!! Example: From Newton’s second law (F=ma) (a second order DE!!!)

THE PENDULUM • Gravity provides the restoring force. • For a pendulum of length L, the arc length is s=Lθ • θ is increasing in the counterclockwise direction • The velocity and acceleration along the arc are s’=L θ’ and s’’=L θ’’, respectively.

THE PENDULUM Using Newton’s 2 nd Law: Without friction r=0. What do you think is the solution to this DE?