MATH 137 TRIGONOMETRY AND ANALYTICAL GEOMETRY 6 3

MATH 137 TRIGONOMETRY AND ANALYTICAL GEOMETRY 6. 3 Trigonometric Functions of Real Numbers

Objectives • Section 6. 2 cont. • Introduce Fundamental Identities and Co-Functions • Section 6. 3 • Understand the importance of the Unit Circle • To know and be able to identify the special values in all quadrants of the Unit Circle. • Understand the negative and even and odd identities. • To know the graphs, domain, range and period of the six basic Trig. Functions

6. 2 cont. The Fundamental Identities 1) Reciprocal Identities 2) Tangent and Cotangent Identities 2) The Pythagorean Identities

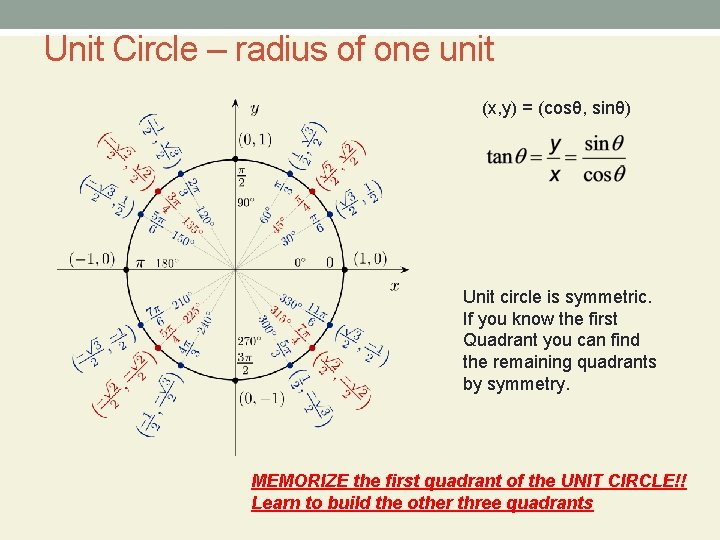
6. 3 Trigonometric Functions of Real Numbers Unit Circle • Unit Circle has a radius of one unit. • =(cosθ, sinθ) P(t)=(x, y) =(cosθ, sinθ) t is the length of the arc intercepted by θ in radians or the radian measure of angle θ (i. e. t=θ) t θ Point on the unit circle that corresponds to t Coordinates of The point x and y correspond to cosine and can be used to find all six Trig. Functions.

Unit Circle - Common Angles 0 o =0 30 o = π/6 45 o = π/4 60 o = π/3 Sin θ 0 1 2 √ 2 2 √ 3 2 1 Cos θ 1 √ 3 2 √ 2 2 1 2 0 Tan θ 0 √ 3 3 1 √ 3 undef ined sin + cos tan - All (+) sin cos – tan + sin cos + tan - 90 o = π/2

Unit Circle – radius of one unit (x, y) = (cosθ, sinθ) Unit circle is symmetric. If you know the first Quadrant you can find the remaining quadrants by symmetry. MEMORIZE the first quadrant of the UNIT CIRCLE!! Learn to build the other three quadrants

Problem Solving Unit Circle Example 1. Let P be the point on the unit circle that corresponds to t. Find the coordinates of P and the exact values of the six trigonometric functions a. At t = 2π/3 b. At t = 3π/2 c. At t = 7π/2 d. At t = -7π/6

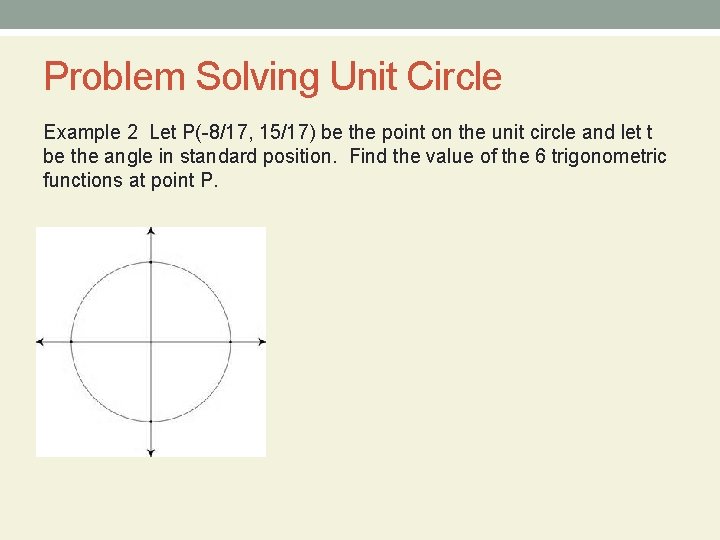
Problem Solving Unit Circle Example 2 Let P(-8/17, 15/17) be the point on the unit circle and let t be the angle in standard position. Find the value of the 6 trigonometric functions at point P.

Instructor Choice

Formula for Negatives • sin(-t) = -sin(t) • csc(-t) = -csc(t) cos(-t) = cos(t) sec(-t) = csc (t) tan(-t) = -tan(t) cot(-t) = -cot(t) Therefore cos and sec are even functions, sin, csc, tan and cot are odd functions. Remember: The graphs of even functions reflect over the y-axis and odd functions reflect over the origin.

Problem Solving Example 3: Use a formula for negatives to find the exact value: a) Sin(-150 o) b) cot(-225 o) c) cos(-π/4) d) csc(-45 o)

Periodic Functions • Functions that repeat are called periodic functions. • Sine and Cosine repeat every 2π or one complete revolution on the unit circle • We say the Period of Sine and Cosine equals 2π If n is any integer then, Example 4: Find a. sin(9π/4) b. cos(15π/3)

Graph the function y = sin(x) See table of Graphs on Page 387

Graph the function y = cos(x)

Graph the function y = tan(x)

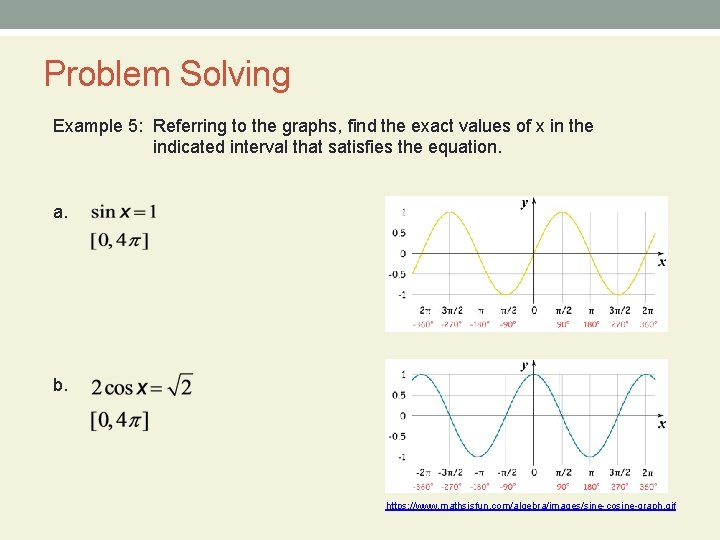
Problem Solving Example 5: Referring to the graphs, find the exact values of x in the indicated interval that satisfies the equation. a. b. https: //www. mathsisfun. com/algebra/images/sine-cosine-graph. gif

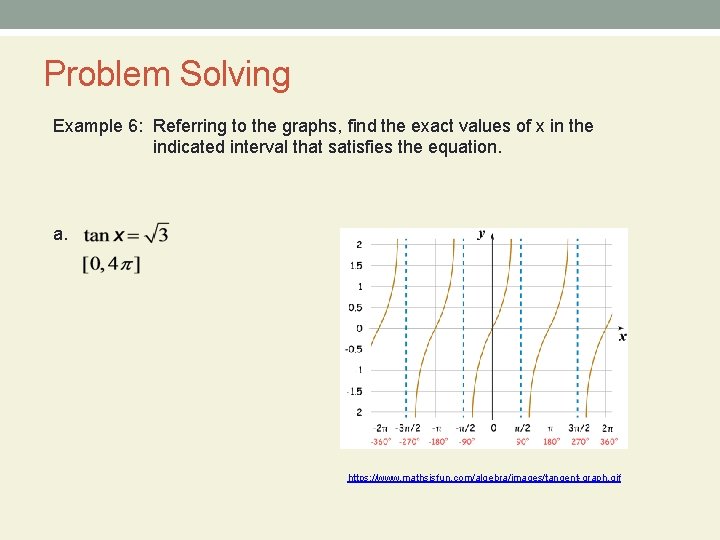
Problem Solving Example 6: Referring to the graphs, find the exact values of x in the indicated interval that satisfies the equation. a. https: //www. mathsisfun. com/algebra/images/tangent-graph. gif

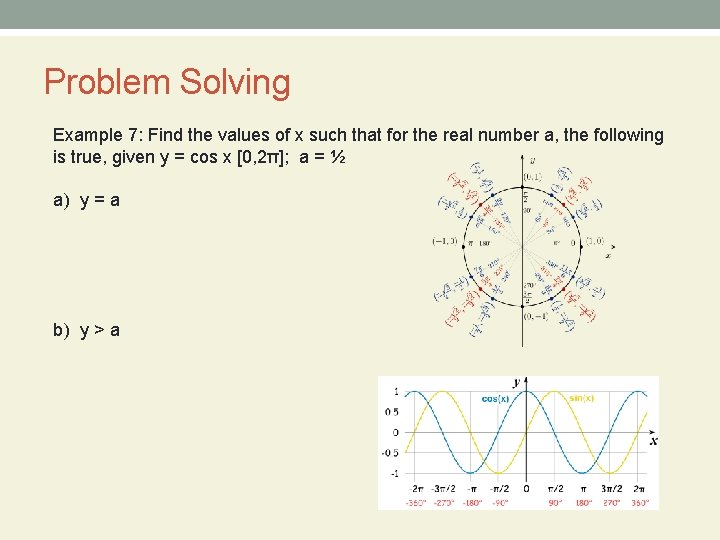
Problem Solving Example 7: Find the values of x such that for the real number a, the following is true, given y = cos x [0, 2π]; a = ½ a) y = a b) y > a

Homework • Web. Assign HW 6. 3 due Monday 1/29 • HW 6. 2 due Wednesday 1/25 • • Quiz 1 – In Class, Thursday, 1/25, No Calculator, (20 Points) • Unit Circle Quiz Tuesday, 1/30 at start of class. (IC – 5 points) • Pre-Read 6. 4