MATH 1314 College Algebra Matrices Matrices Section Notes

MATH 1314 College Algebra Matrices

Matrices Section Notes: • A matrix is a _____ of numbers. rectangular array • The numbers in a matrix are called ______ or _______. entries terms • An _____ matrix is a matrix that represents a system augmented of equations. Gaussian • The _____ Method uses these matrices to solve a system of linear equations. (Review in textbook. ) row operations • This method relies on ______ to eliminate any entry in the matrix. • Only 3 Row Operations are used on a matrix: Switch ü ____ any two rows. Multiply ü ____ any row by a nonzero constant. Add ü ____ any two rows, …or add a non-zero constant multiple of one row to another.

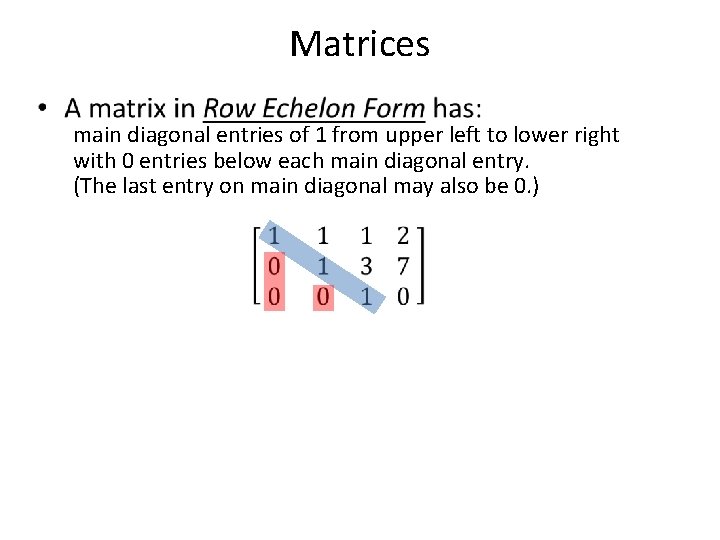
Matrices • main diagonal entries of 1 from upper left to lower right with 0 entries below each main diagonal entry. (The last entry on main diagonal may also be 0. )

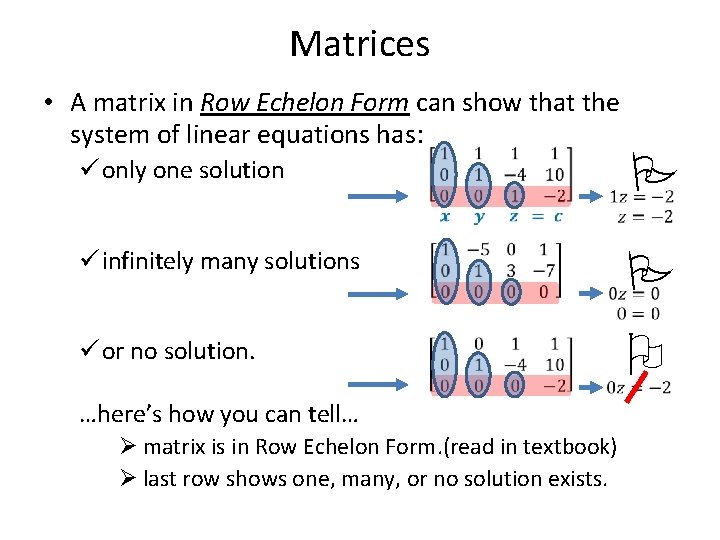
Matrices • A matrix in Row Echelon Form can show that the system of linear equations has: ü only one solution ü infinitely many solutions ü or no solution. …here’s how you can tell… P P Ø matrix is in Row Echelon Form. (read in textbook) Ø last row shows one, many, or no solution exists. O

Matrices • P

Matrices •

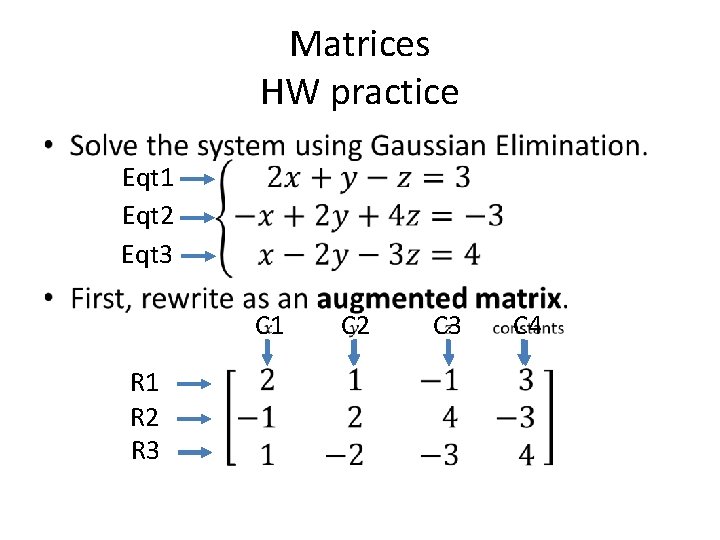
Matrices HW practice • Eqt 1 Eqt 2 Eqt 3 C 1 C 2 C 3 C 4 R 1 R 2 R 3

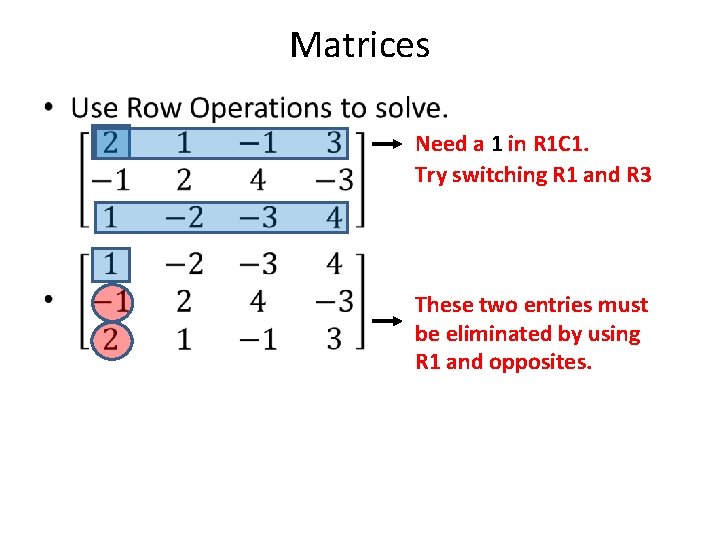
Matrices • Need a 1 in R 1 C 1. Try switching R 1 and R 3 These two entries must be eliminated by using R 1 and opposites.

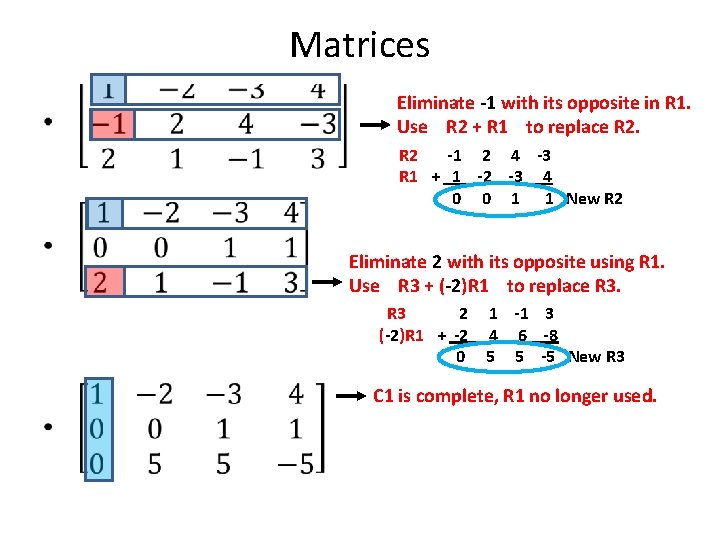
Matrices • Eliminate -1 with its opposite in R 1. Use R 2 + R 1 to replace R 2 -1 2 4 -3 R 1 + 1 -2 -3 4 0 0 1 1 New R 2 Eliminate 2 with its opposite using R 1. Use R 3 + (-2)R 1 to replace R 3 2 1 -1 3 (-2)R 1 + -2 4 6 -8 0 5 5 -5 New R 3 C 1 is complete, R 1 no longer used.

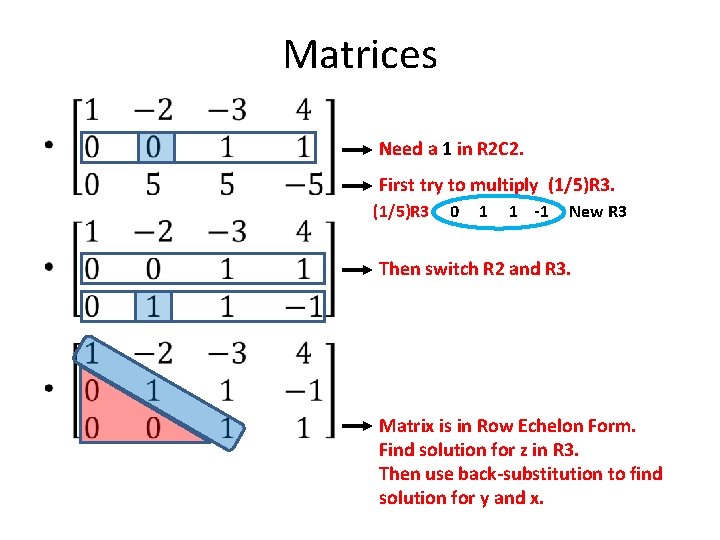
Matrices • Need a 1 in R 2 C 2. First try to multiply (1/5)R 3 0 1 1 -1 New R 3 Then switch R 2 and R 3. Matrix is in Row Echelon Form. Find solution for z in R 3. Then use back-substitution to find solution for y and x.

Matrices Variable coefficients •

Matrices HW practice •

Matrices • Translating a written application problem to equations: 1. Read carefully. (read two or more times) 2. Identify and label variables and number of equations. ü variables: The last question gives you a hint. ü equations: How many quantity totals are stated? 3. Form system of equations from variables and quantity totals.

Matrices • Section 8. 2: Exercise #81 -College Algebra e-text 1. Read. 2. Variables and Totals: ü Variables: Delta x, Beta y, Sigma z ü Totals(equations): painting, drying, polishing

Matrices • Section 8. 2: Exercise #81 -College Algebra e-text 3. Form equations: • • • Painting hours Drying hours Polishing hours Now form augmented matrix to solve. Total hours

MATH 1314 College Algebra Unit 1 Functions and their Graphs Section: 3. 1

Functions Section : _____ • input output domain range independent

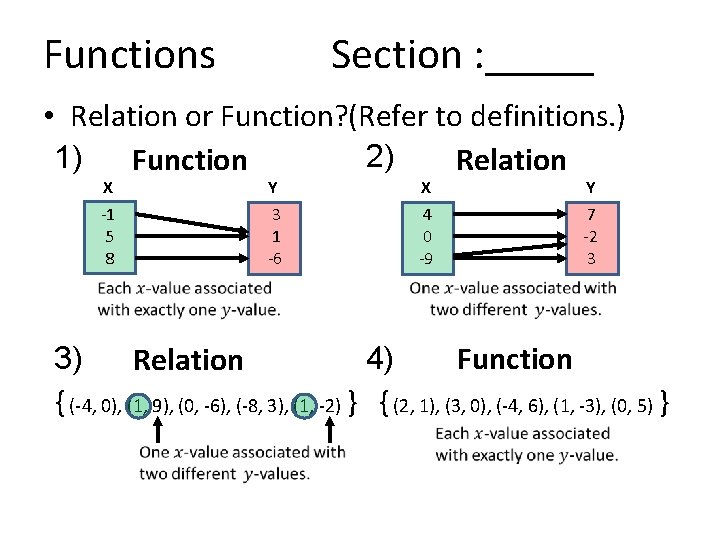
Functions Section : _____ • Relation or Function? (Refer to definitions. ) 2) 1) Relation Function X Y -1 5 8 3 1 -6 4 0 -9 7 -2 3 4) Function 3) Relation { (-4, 0), (1, 9), (0, -6), (-8, 3), (1, -2) } { (2, 1), (3, 0), (-4, 6), (1, -3), (0, 5) }

Functions Section : _____ • 1) 2)

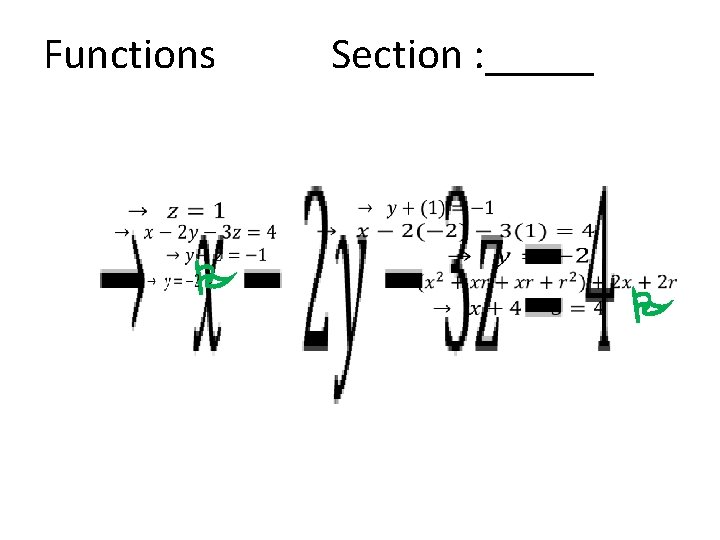
Functions Section : _____ • P

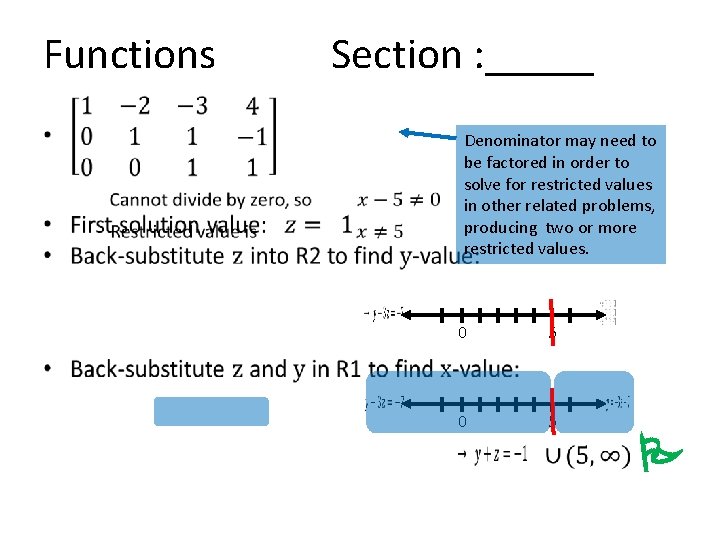
Functions Section : _____ • Denominator may need to be factored in order to solve for restricted values in other related problems, producing two or more restricted values. 0 0 5 5 P

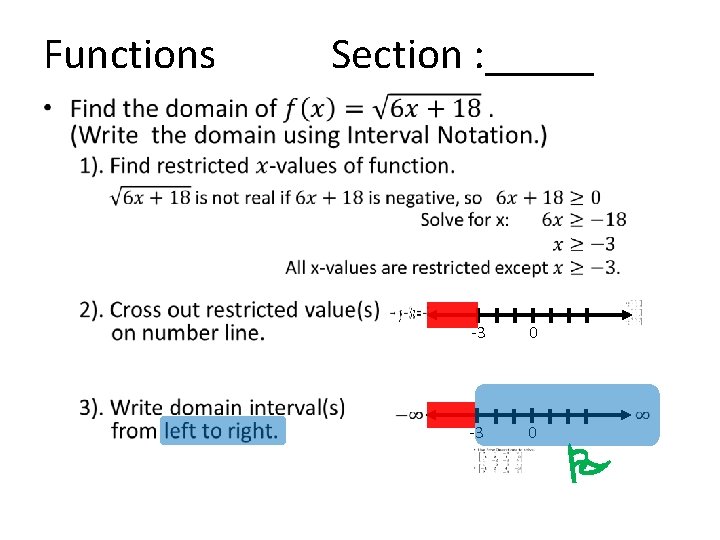
Functions Section : _____ • -3 -3 0 0 P

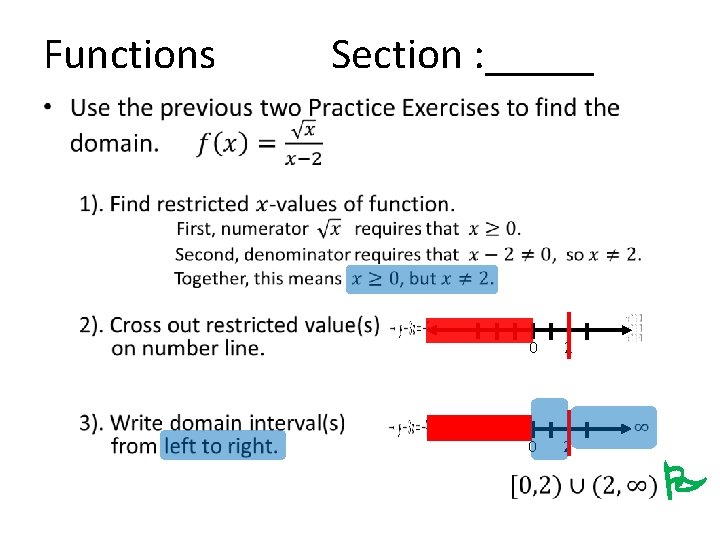
Functions Section : _____ • 0 0 2 2 P

MATH 1314 College Algebra Functions and their Graphs Section: 3. 2

Graphs of Functions Section : ____ • A function can be identified from its graph by Vertical Line the ______Test. • The Vertical Line Test states: if a vertical line intersects a graph _______, the graph more than once is __________. not a graph of a function • Is this the graph of a function? A vertical line intersects the graph only once. YES! A vertical line intersects the graph more than once. NO!

Graphs of Functions Section : ____ •

Graphs of Functions Section : ___ •

Graphs of Functions Section : ___ • Equation Editor Yes X-variable TI-83/84 : P 2) Press 2 nd GRAPH for TABLE. Exponent

Graphs of Functions Section : ___ • P

Graphs of Functions Section : ___ • When solving Quadratic equations, always write in Standard Form first. P

Graphs of Functions Section : ___ • P

Graphs of Functions Section : ___ • Factoring is needed to solve the Quadratic equation. P

MATH 1314 College Algebra Unit 1 Library of Functions Section: 3. 4

Library of Functions Section : ____ • This section covers several basic functions to begin the main study of this course. • Study and learn all properties and graphs for the functions listed in this section that you were assigned. • The next section will cover a collection of techniques called Transformations to graph functions similar to these basic functions. • After completing the work in this section, your goal is to successfully: – recognize and sketch the graph of each function, – identify the Domain and Range of each function. • If you do not meet this goal, you will need to review this section until you can in order to prepare for Section 3. 5.

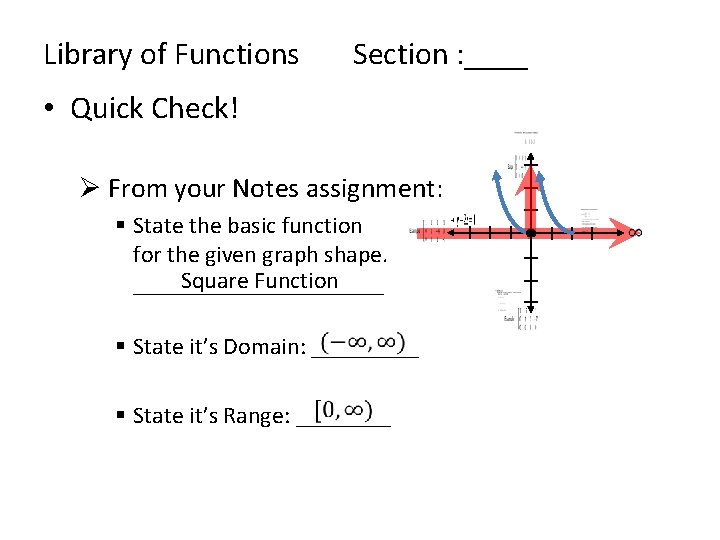
Library of Functions Section : ____ • Quick Check! Ø From your Notes assignment: § State the basic function for the given graph shape. Square Function ___________ § State it’s Domain: _____ § State it’s Range: ____

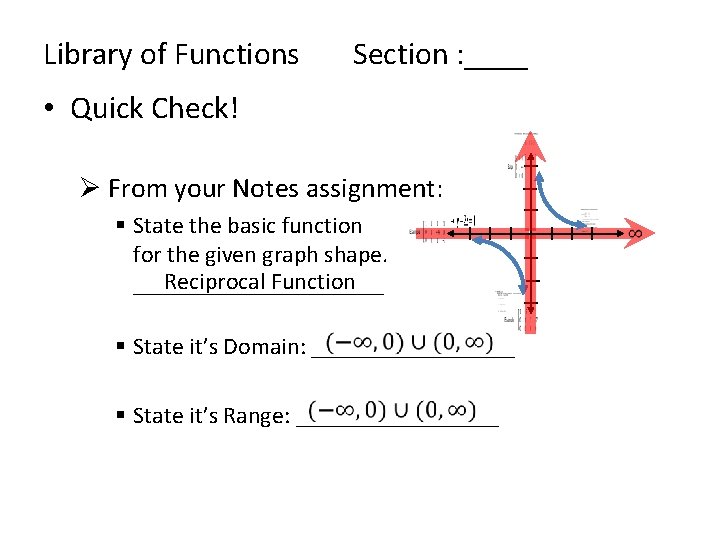
Library of Functions Section : ____ • Quick Check! Ø From your Notes assignment: § State the basic function for the given graph shape. Reciprocal Function ___________ § State it’s Domain: _________ § State it’s Range: _________

Library of Functions Section : ____ • Quick Check! Ø From your Notes assignment: § State the basic function for the given graph shape. Cube Root Function ___________ § State it’s Domain: _____ § State it’s Range: ____

Library of Functions Section : ____ • Quick Check! Ø From your Notes assignment: § State the basic function for the given graph shape. Identity Function ___________ § State it’s Domain: _____ § State it’s Range: ____

Library of Functions Section : ____ • 5 - 5 [[ 5 - 3 P

Library of Functions Section : ____ • P P

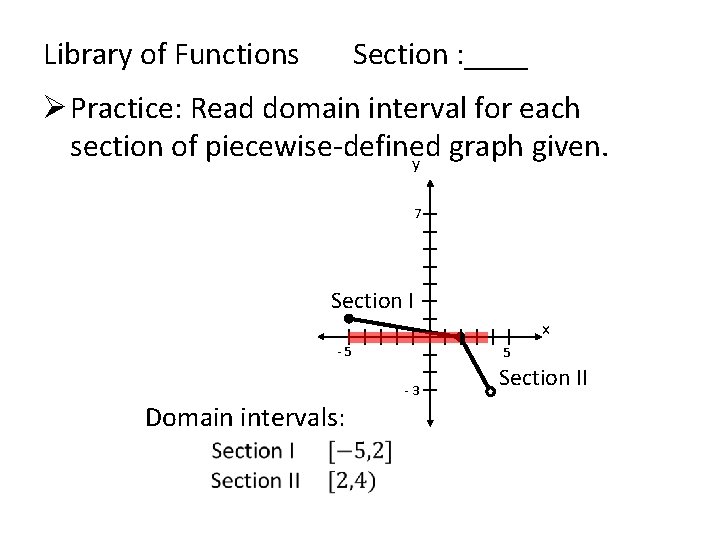
Library of Functions Section : ____ Ø Practice: Read domain interval for each section of piecewise-defined graph given. y 7 Section I x - 5 5 - 3 Domain intervals: Section II

Library of Functions Section : ____ • y 7 Domain for Left line segment is: - 5 P - 3 P 5 x

Review and Complete HW 3. 4 -Library of Functions

MATH 1314 College Algebra Unit 1 Transformations Section: 3. 5

Transformations • Section : ____ Transformations Reflections Stretch/Compress Shifts three vertically horizontally vertically

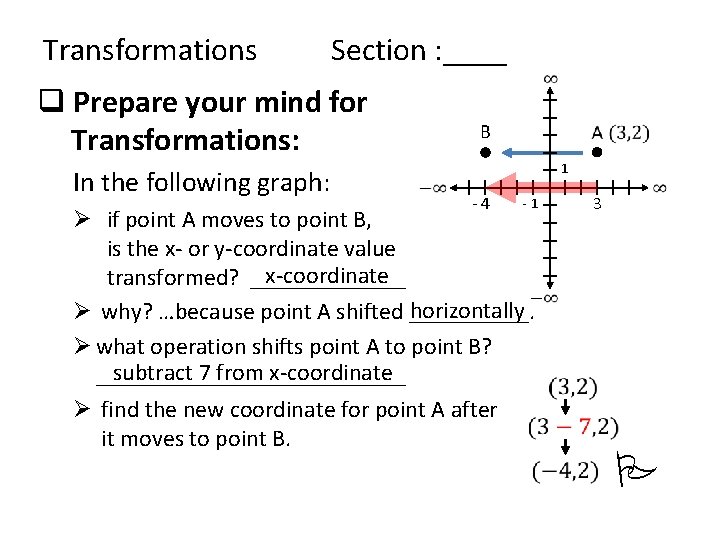
Transformations Section : ____ q Prepare your mind for Transformations: In the following graph: B 1 - 4 - 1 Ø if point A moves to point B, is the x- or y-coordinate value x-coordinate transformed? _______ horizontally Ø why? …because point A shifted _____. Ø what operation shifts point A to point B? subtract 7 from x-coordinate _____________ Ø find the new coordinate for point A after it moves to point B. 3 P

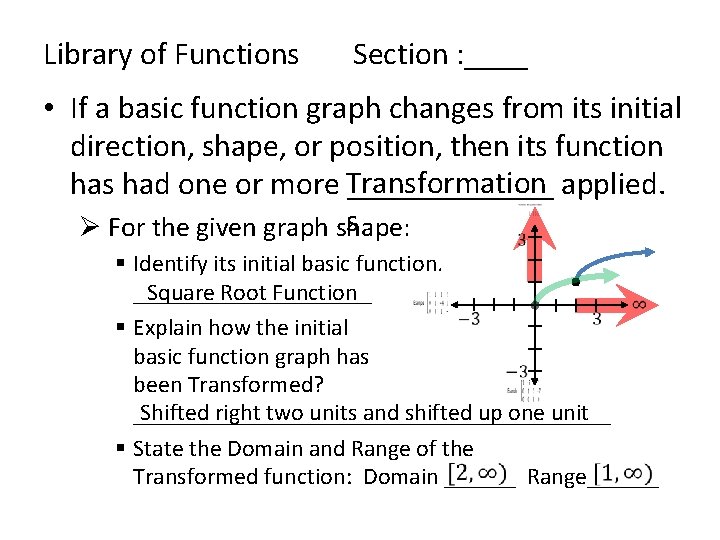
Library of Functions Section : ____ • If a basic function graph changes from its initial direction, shape, or position, then its function Transformation has had one or more _______ applied. s Ø For the given graph shape: § Identify its initial basic function. Square Root Function __________ § Explain how the initial basic function graph has been Transformed? Shifted right two units and shifted up one unit ____________________ § State the Domain and Range of the Transformed function: Domain ______ Range______

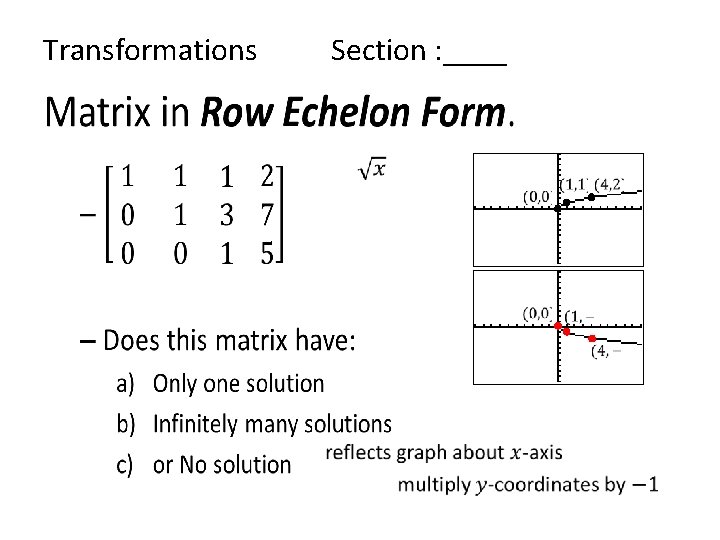
Transformations Section : ____ •

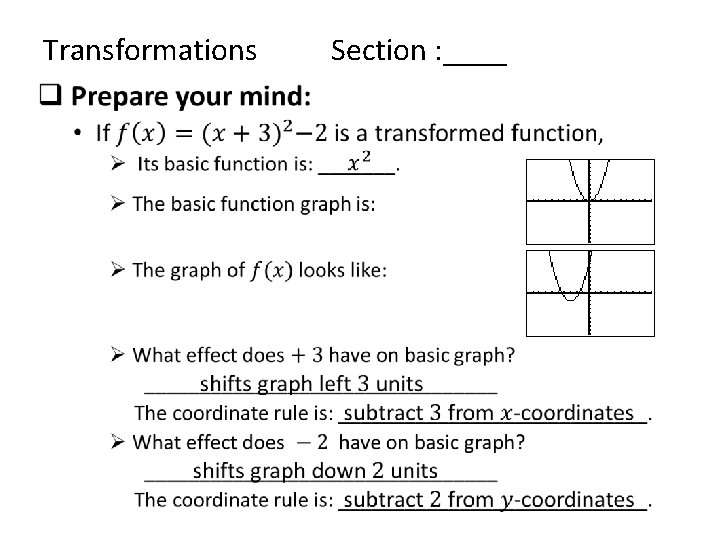
Transformations Section : ____ •

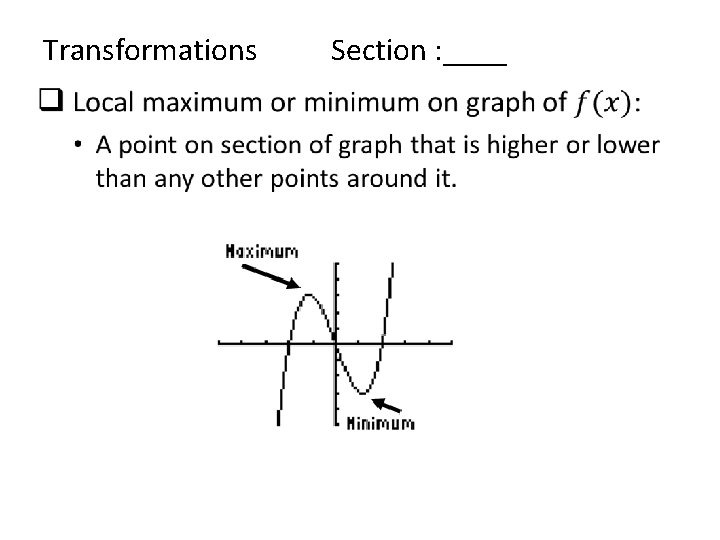
Transformations • Section : ____

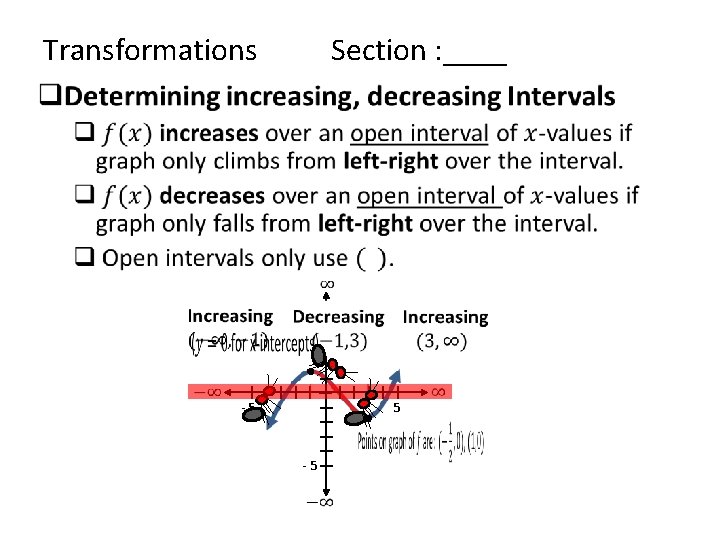
Transformations Section : ____ • 5 - 5 5 - 5

Transformations • Section : ____

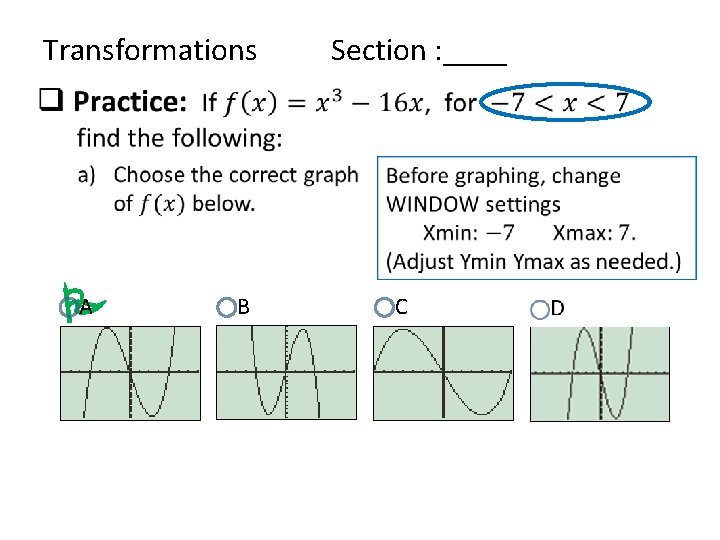
Transformations Section : ____ • A P B C

Transformations Section : ____ • P P

End - Unit 1 Complete all Ch 3 assignments in time to take Ch 3 Exam by Due Date.