MATH 0322 Intermediate Algebra Unit 4 Review Slope

MATH 0322 Intermediate Algebra Unit 4 Review: Slope and Slope-Intercept

Slope and Slope-Intercept Form • slope

Slope and Slope-Intercept Form • increases decreases constant

Slope and Slope-Intercept Form •


MATH 0322 Intermediate Algebra Unit 4 Section 3. 5 Point-Slope Equation

Point-Slope Form •

Point-Slope Form • Standard Form Vertical Line Form Horizontal Line Form Slope-Intercept Form Point-Slope Form

Point-Slope Form •

Point-Slope Form • P P P

Point-Slope Form • P P

Point-Slope Form • P P

Point-Slope Form • P P

Point-Slope Form • P P

Point-Slope Form • P P

Point-Slope Form • P

Point-Slope Form • P

Complete and Practice HW 3. 5


MATH 0322 Intermediate Algebra Unit 4 Solving Systems of Linear Equations (Graphing Method) Section: 4. 1
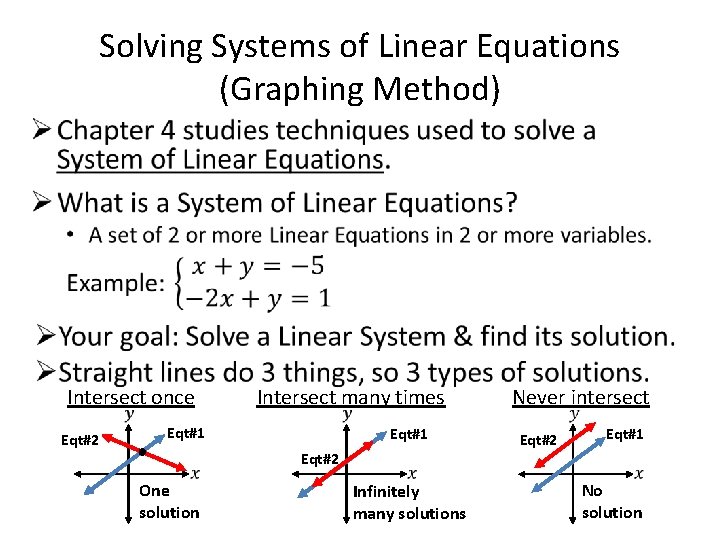
Solving Systems of Linear Equations (Graphing Method) • Intersect once Eqt#2 Intersect many times Eqt#1 One solution Eqt#1 Eqt#2 Infinitely many solutions Never intersect Eqt#2 Eqt#1 No solution

Solving Systems of Linear Equations (Graphing Method) • Equation #1 or Equation #2 goes here.

• Solving Systems of Linear Equations (Graphing Method) P O Not a solution. P

• Solving Systems of Linear Equations (Graphing Method) Yes P P P
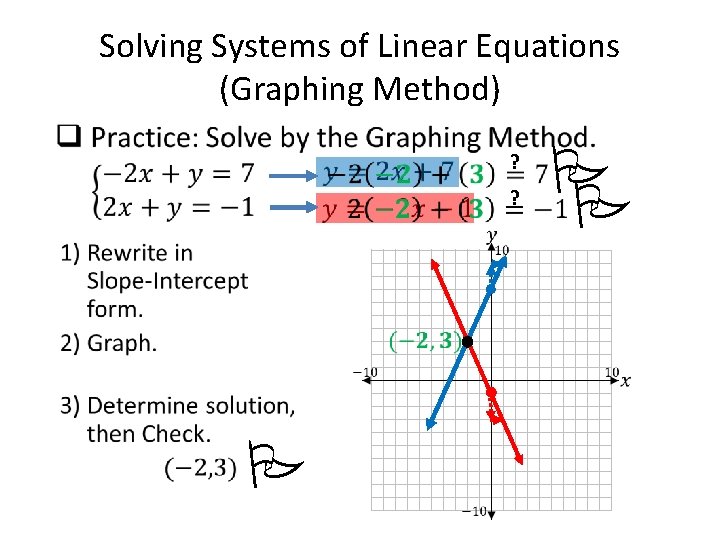
• Solving Systems of Linear Equations (Graphing Method) ? ? P P
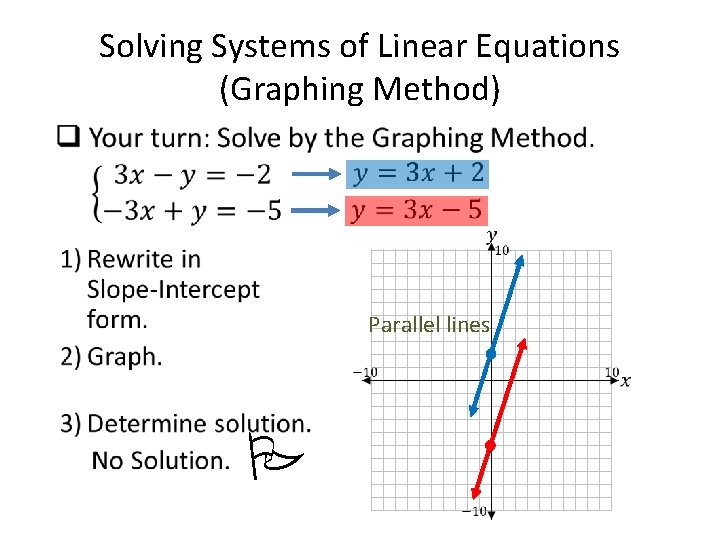
• Solving Systems of Linear Equations (Graphing Method) Parallel lines P
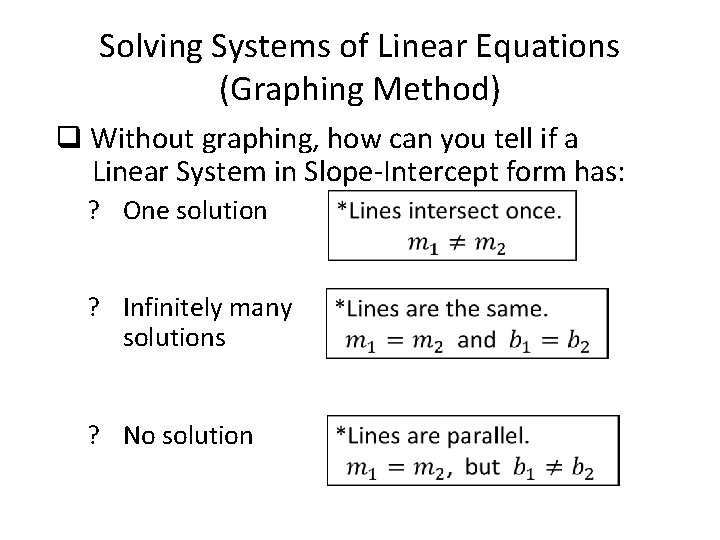
Solving Systems of Linear Equations (Graphing Method) q Without graphing, how can you tell if a Linear System in Slope-Intercept form has: ? One solution ? Infinitely many solutions ? No solution

• Solving Systems of Linear Equations (Graphing Method) P

Graphing Method Complete and Practice HW 4. 1


MATH 0322 Intermediate Algebra Unit 4 Solving Systems of Linear Equations (Substitution Method) Section: 4. 2

Solving Systems of Linear Equations (Substitution Method) Ø This section introduces the Substitution Method: an algebraic method that substitutes the value of a variable from one equation into the other equation to solve a Linear System. Ø To solve a Linear System using this method: 1) Isolate a variable. (simplest one) 2) Substitute into other equation, solve 1 st solution. 3) Back-substitute into an original equation, solve 2 nd solution, then Check.
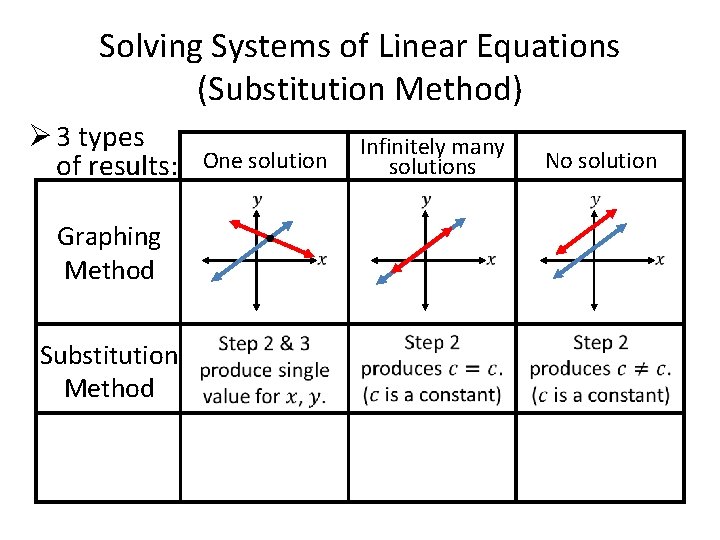
Solving Systems of Linear Equations (Substitution Method) Ø 3 types of results: One solution Infinitely many solutions Graphing Method Substitution Method No solution

• Solving Systems of Linear Equations (Substitution Method) P P

• Solving Systems of Linear Equations (Substitution Method) P P

• Solving Systems of Linear Equations (Substitution Method) P

• Solving Systems of Linear Equations (Substitution Method) ?

• Solving Systems of Linear Equations (Substitution Method) ? ?

• Solving Systems of Linear Equations (Substitution Method)

• Solving Systems of Linear Equations (Substitution Method) ?

Solving Systems of Linear Equations (Substitution Method) • P

• Solving Systems of Linear Equations (Substitution Method) P System has no solution.

Substitution Method Complete and Practice HW 4. 2


MATH 0322 Intermediate Algebra Unit 4 Solving Systems of Linear Equations (Addition Method) Section: 4. 3

Solving Systems of Linear Equations (Addition Method) •

Solving Systems of Linear Equations (Addition Method) •
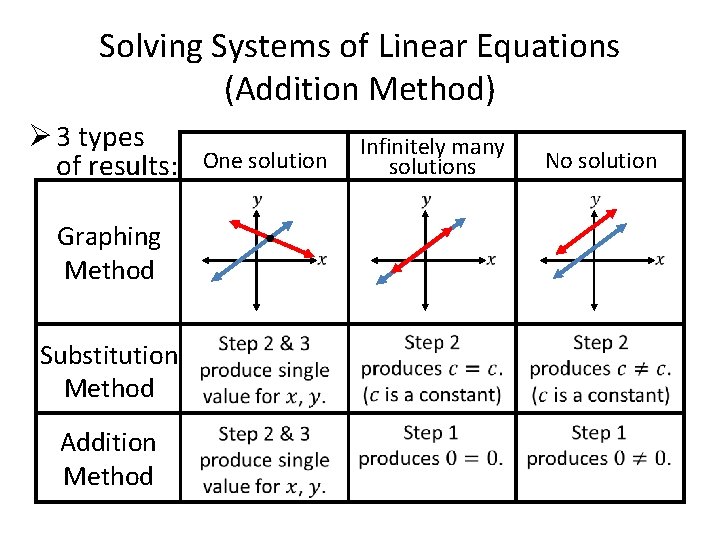
Solving Systems of Linear Equations (Addition Method) Ø 3 types of results: One solution Infinitely many solutions Graphing Method Substitution Method Addition Method No solution

• Solving Systems of Linear Equations (Addition Method) Yes P P P
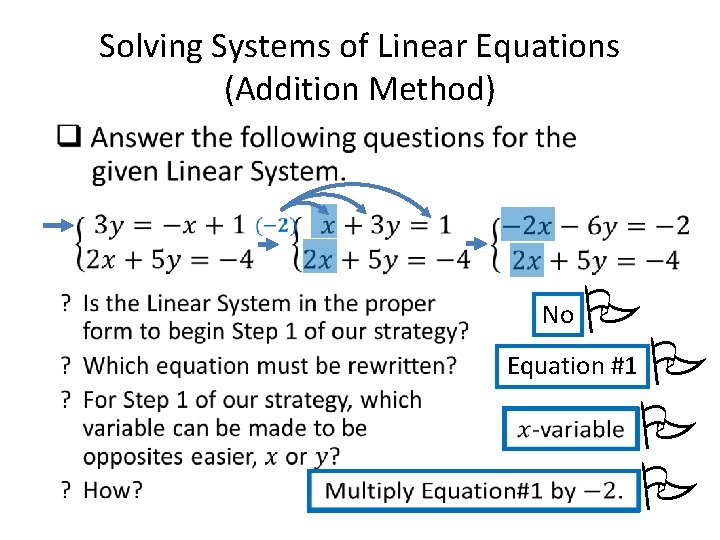
Solving Systems of Linear Equations (Addition Method) • No P P Equation #1

• Solving Systems of Linear Equations (Addition Method) Step 1) Step 2) Step 3) P

• Solving Systems of Linear Equations (Addition Method) Step 1) Infinitely many solutions P

Solving Systems of Linear Equations (Addition Method) • Step 1) Yes Step 2) Step 3) P P

Addition Method Complete and Practice HW 4. 3

MATH 0322 Intermediate Algebra Unit 4 Appendix B: Matrices
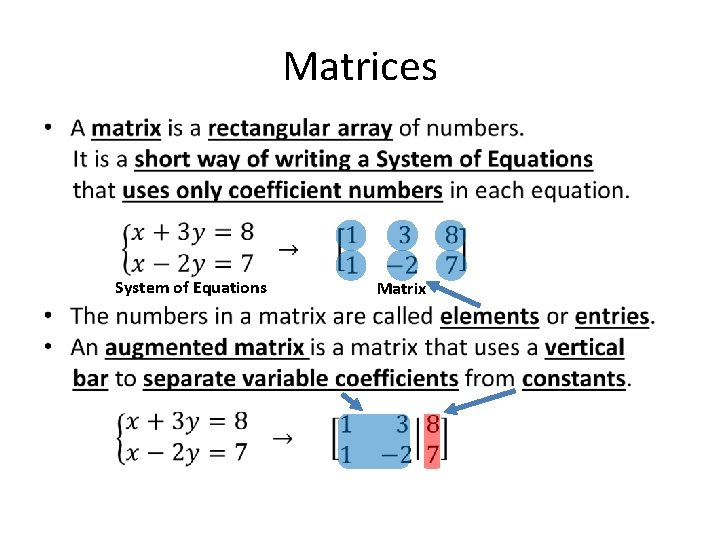
Matrices • System of Equations Matrix

Matrices •

Matrices • Row-Echelon form: Ø If last row looks like this, o System has One Solution. o System is Consistent. o Equations are Independent. Ø If last row looks like this, o System has Infinitely Many Solutions. o System is Consistent. o Equations are Dependent. Ø If last row looks like this, o System has No Solution. o System is Inconsistent.
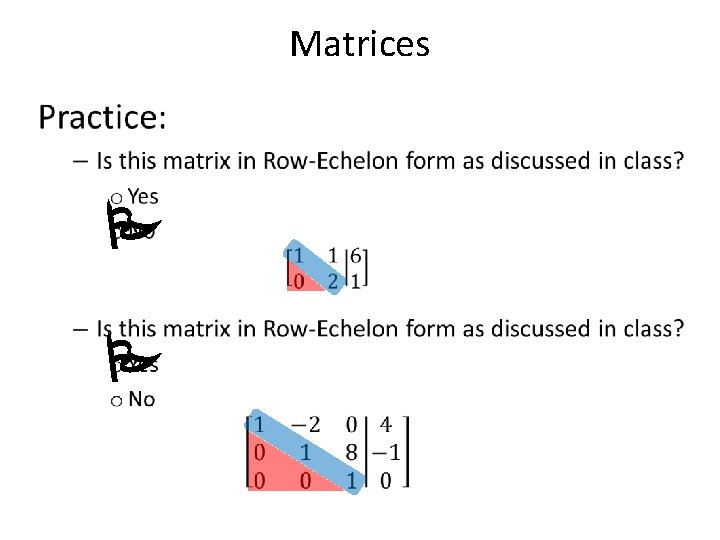
Matrices • P P

Matrices •

Matrices • To solve a System of Equations using matrices: 1) Write augmented matrix. 2) Apply Row Operations to get Row-Echelon form. 3) Rewrite rows as equations, then Back-Substitute to determine solution set.

Matrices • P P

Matrices • P

Matrices • P

Matrices • P

Matrices •

Matrices •

Matrices •

Matrices • P

• Matrices 2) Apply Row Operations to get Row-Echelon form.

Appendix B: Matrices Complete and Practice


Point-Slope Form •
- Slides: 73