MATERI 3 TRANSPORTASI TRANSPORTASI ANGKUTAN Masalah transportasi membicarakan

MATERI - 3 TRANSPORTASI

TRANSPORTASI (ANGKUTAN) • Masalah transportasi membicarakan cara pendistribusian suatu komoditi dari sejumlah sumber (origin) ke sejumlah tujuan (destination). • Sasarannya adalah – mencari pola pendistribusian dan banyaknya komoditi yang diangkut dari masing sumber ke masing tujuan – yang meminimalkan ongkos angkut secara keseluruhan, dengan kendala yang ada.

SKENARIO TRANSPORTASI • Masalah transportasi diformulasikan berdasarkan skenario sebagai berikut : – Ada sumber/daerah asal (origin) dengan kapasitas (supply) maksimumnya. – Ada tujuan (destination) dengan permintaan (demand) minimumnya. – Ada jalur angkutan dari setiap sumber ke setiap tujuan beserta ongkos angkut satuan. (Ongkos sifatnya linier proporsional terhadap jarak) – Ada satu macam komoditi saja yang diangkut – Meminimalkan ongkos angkut. – Adanya fungsi sasaran (objective function) yang diasumsikan linear.

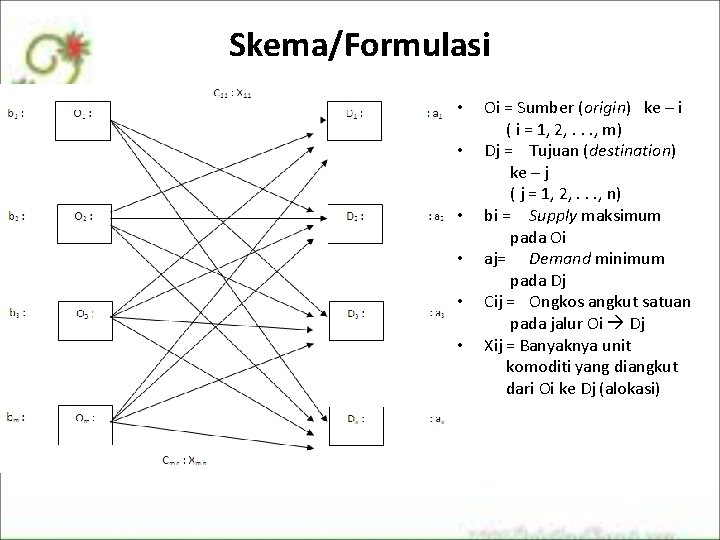
Skema/Formulasi • Oi = Sumber (origin) ke – i ( i = 1, 2, . . . , m) • Dj = Tujuan (destination) ke – j ( j = 1, 2, . . . , n) • bi = Supply maksimum pada Oi • aj= Demand minimum pada Dj • Cij = Ongkos angkut satuan pada jalur Oi Dj • Xij = Banyaknya unit komoditi yang diangkut dari Oi ke Dj (alokasi)

Asumsi • Diasumsikan : i. ii. Linieritas, merupakan biaya angkut, yang berbanding lurus (proporsional) dengan banyaknya komoditi yang diangkut dari origin ke destination. Hanya ada satu jenis komoditi yang diangkut • Asumsi (i) berakibat masalah transportasi termasuk dalam kategori masalah program linear, Sehingga cara menyelesaikannya bisa memanfaatkan metode yang sudah lasim dikenal, seperti yang akan dijabarkan kemudian. • Asumsi (ii) berakibat setiap destination bisa menerima kiriman dari setiap origin.

Formulasi Model Matematika • Berdasarkan skenario di atas, maka formulasi model matematika masalah transportasi adalah sebagai berikut: • Mencari xij ≥ 0 (i = 1, 2, …, m; j = 1, . . n) yang meminimalkan fungsi sasaran (ongkos angkut total) dengan kendala (constraint) : • Ketaksamaan (2) disebut kendala supply dan ketaksamaan (3) disebut kendala demand. • Fungsi f pada persamaan (1) disebut fungsi sasaran (objective function).

Penyajian Data • Penyajian data masalah transportasi dituangkan dalam tabel berikut :

Solusi Keadaan Setimbang • Jika yaitu total supply komoditi pada origin sama dengan total demand pada destination, maka masalah transportasi dikatakan setimbang. Dalam kasus setimbang, semua kendala, baik kendala supply maupun kendala demand berbentuk persamaan, sebagai berikut : Akibatnya banyaknya variabel basis adalah m+n-1, sebab m+n-1 merupakan banyaknya persamaan yang saling independen. Oleh karena itu penyelesaian fisibel basis (pfb) terdiri atas m+n-1 variabel basis.

Penyelesaian Masalah Transportasi • Untuk mencari solusi optimal (minimal) masalah transportasi, dikerjakan dengan 3 langkah: Langkah I : Menyusun solusi awal (Tabel Awal) • Maksud menyusun solusi awal: untuk mencari pfb. • Dasar hukum (dalil) : Hukum 1: Tabel transportasi akan memberikan suatu pfb bila dalam setiap pengisian alokasi dipilih alokasi yang memaksimalkan kotak dengan batasan supply & demand. Hukum 2: pfb paling tidak memuat satu solusi optimal. • Berdasarkan kedua hukum di atas, ada beberapa metode peyusunan tabel awal antara lain :

Cara 1: Metode Sudut Barat Laut (North West Corner) • Metode ini dikerjakan sebagai berikut : a) Mengisi alokasi x 11 sebanyak mungkin dengan batasan supply b 1 dan demand a 1. Jadi x 11 = min {a 1, b 1}. a) Setelah alokasi x 11 diisi, maka kolom ke 1 penuh atau baris ke 1 penuh. b) Jika kolom ke 1 penuh dan baris ke 1 belum penuh, maka langkah selanjutnya mengisi alokasi x 12 sebanyak mungkin dengan batasan supply b 1 dan demand a 2. c) Jika baris ke 1 penuh dan kolom ke 1 belum penuh maka langkah selanjutnya mengisi alokasi x 21 sebanyak mungkin dengan batasan supply b 2 dan demand a 1. d) Jika baris ke 1 penuh dan kolom ke 1 penuh, maka langkah selanjutnya mengisi alokasi x 22 dengan batasan supply b 2 dan demand a 2. • Langkah langkah ini bisa dilanjutkan sampai semua baris dan kolom penuh, dan akhirnya diperoleh m+n-1 alokasi, yang menurut kedua hukum di atas salah satunya merupakan solusi optimal.

Cara 2 : Metode Ongkos Terkecil (Least Cost Method) • Metode ini dikerjakan sebagai berikut : a) Dipilih ongkos angkut satuan cij terkecil/ termurah, diisi dengan alokasi sebanyak mungkin dengan batasan supply bi dan demand aj. Kalau ada beberapa cij termurah, tentukan salah satu. a) Langkah a) dikerjakan berulang dengan mengabaikan cij pada kotak yang sudah terisi pada langkah sebelumnya, sampai akhirnya diperoleh sejumlah m+n 1 kotak isi. • Metode North West Corner lebih mudah dikerjakan dari pada metode lainnya, tetapi solusi awal pada umumnya masih jauh dari optimal karena belum memperhitungkan ongkos angkut cij. Hal ini berbeda dengan metode Least-Cost Method, yang sudah memperhitungkan ongkos angkut satuan cij.

Langkah II : Uji Optimalitas • Metode Stepping-Stone (Metode Batu Loncat). Uji optimalitas metode steppingstone dikerjakan sebagai berikut : a) Untuk setiap kotak kosong xij dicari lintasan horisontal & vertikal (tertutup/loop) melewati kotak yang sudah isi. Loop ini selalu bisa diperoleh, karena kita sudah mempunyai m+n 1 kotak isi. Sebagai gambaran misalkan kita mempunyai kotak kosong yang mempunyai lintasan tertutup x 13 x 14 x 33 x 13 , maka “opportunity Cost” c 13* didefinisikan sebagai : c 13* = Δf 13, di mana Δf 13 = c 13 – c 14 + c 34 – c 33. Hitunglah opportunity cost cij untuk setiap kotak kosong xij. • Solusi sudah optimal, bila dan hanya bila /jika opportunity cost cij* ≤ 0, untuk semua kotak kosong xij. • Solusi belum optimal, jika terdapat opportunity cost cij* > 0, untuk setiap kotak kosong xij. Jika ini terjadi, maka langkah selanjutnya adalah memperbaiki tabel (langkah III)

Langkah III : Memperbaiki Tabel • Memperbaiki tabel pada dasarnya adalah menentukan variabel basis yang keluar dan sekaligus menentukan variabel baru yang masuk sebagai basis. Caranya sebagai berikut : – Kotak kosong yang diisi (yaitu variabel baru yang masuk sebagai basis) adalah kotak kosong xij yang mempunyai opportunity cost c ij*>0 – Untuk kotak kosong yang terpilih untuk diisi : • Tentukan lintasan tertutup (loop) seperti langkah II (metode steppingstone) dan diberi tanda berselang seling positif negatif mulai dengan kotak kosong terpilih. • Pilih alokasi kotak bertanda negatif paling kecil (paling melarat), itulah alokasi maksimum yang bisa digeser dan masuk kotak terpilih melalui loop tadi. • Tanda negatif berarti alokasi donor • Alokasi donor paling melarat inilah yang menjadi variabel basis yang keluar, sekaligus menjadi kotak kosong pada tabel berikutnya. • Setelah kotak kosong tersebut diisi, kemudian dikerjakan langkah II (uji optimalitas) lagi. Demikian seterusnya sampai diperoleh solusi optimal.

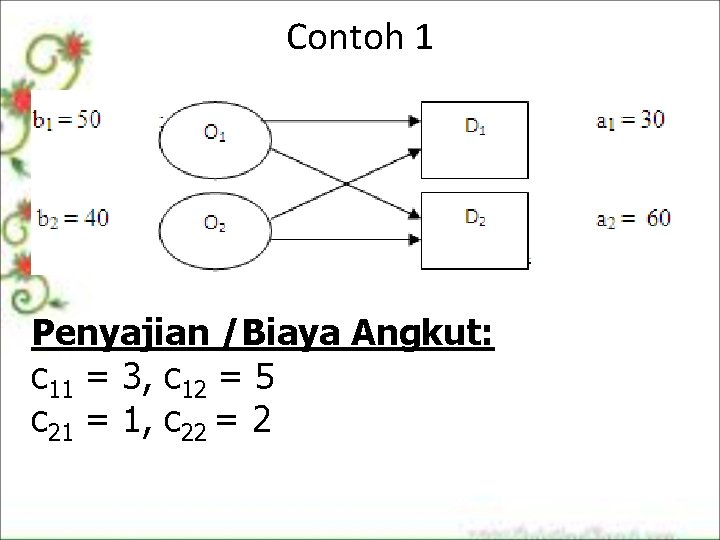
Contoh 1 Penyajian /Biaya Angkut: c 11 = 3, c 12 = 5 c 21 = 1, c 22 = 2

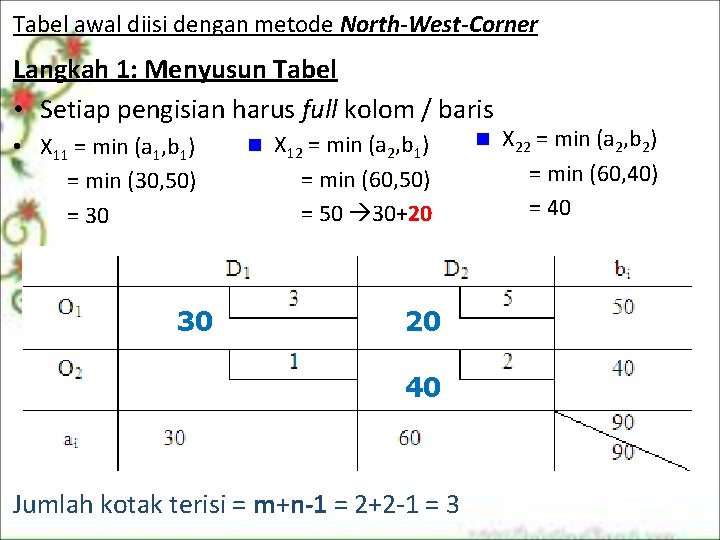
Tabel awal diisi dengan metode North-West-Corner Langkah 1: Menyusun Tabel • Setiap pengisian harus full kolom / baris • X 11 = min (a 1, b 1) = min (30, 50) = 30 30 n X 12 = min (a 2, b 1) = min (60, 50) = 50 30+20 20 40 Jumlah kotak terisi = m+n-1 = 2+2 1 = 3 n X 22 = min (a 2, b 2) = min (60, 40) = 40

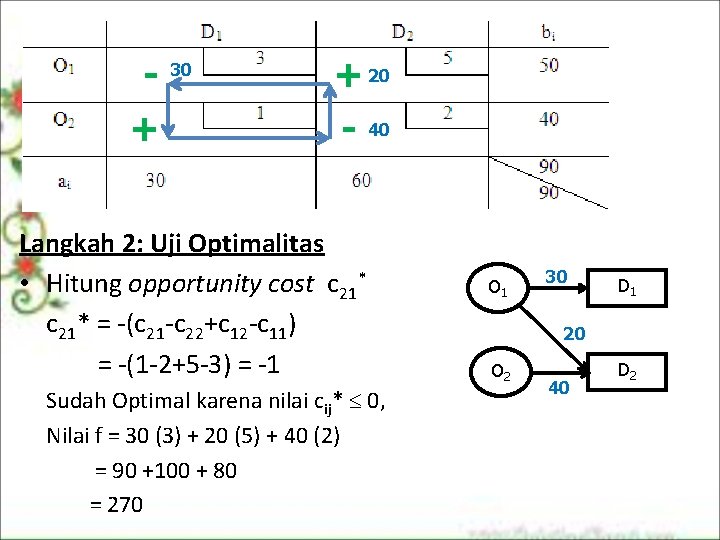
- 30 + + 20 - 40 Langkah 2: Uji Optimalitas • Hitung opportunity cost c 21* = (c 21 c 22+c 12 c 11) = (1 2+5 3) = 1 Sudah Optimal karena nilai cij* 0, Nilai f = 30 (3) + 20 (5) + 40 (2) = 90 +100 + 80 = 270 O 1 30 D 1 20 O 2 40 D 2

Tabel awal diisi dengan metode Least-Cost Method Langkah 1: Menyusun Tabel • Setiap pengisian harus full kolom / baris • Dipilih kotak dgn ongkos angkut satuan cij terkecil / termurah, jika ada yang sama pilih salah satu. • Cij terkecil adalah C 21 = 1, maka kotak 21 diisi dengan x 21 = min(a 1, b 2) = min(30, 40) = 30 • Selanjutnya cari kotak dengan Cij terkecil lagi 50 30 10

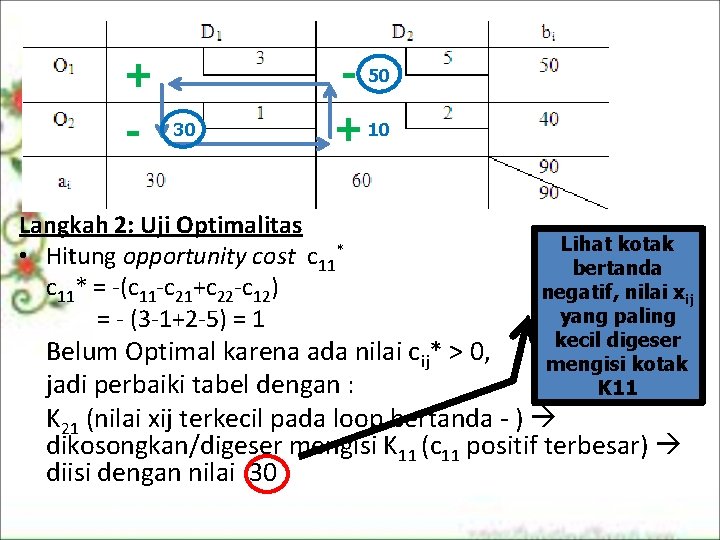
+ - 30 - 50 + 10 Langkah 2: Uji Optimalitas • Hitung opportunity cost c 11* = (c 11 c 21+c 22 c 12) = (3 1+2 5) = 1 Lihat kotak bertanda negatif, nilai xij yang paling kecil digeser mengisi kotak K 11 Belum Optimal karena ada nilai cij* > 0, jadi perbaiki tabel dengan : K 21 (nilai xij terkecil pada loop bertanda ) dikosongkan/digeser mengisi K 11 (c 11 positif terbesar) diisi dengan nilai 30

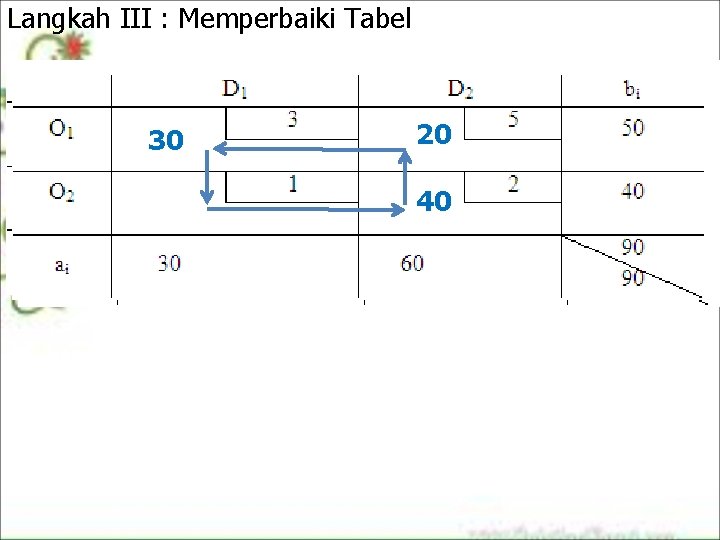
Langkah III : Memperbaiki Tabel 30 30 30 50 20 20 50 30 10 10 40 10

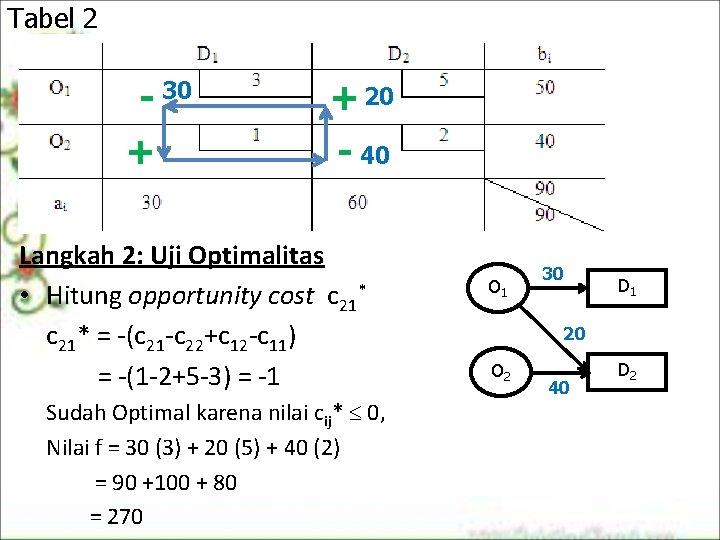
Tabel 2 - 30 + + 20 - 40 Langkah 2: Uji Optimalitas • Hitung opportunity cost c 21* = (c 21 c 22+c 12 c 11) = (1 2+5 3) = 1 Sudah Optimal karena nilai cij* 0, Nilai f = 30 (3) + 20 (5) + 40 (2) = 90 +100 + 80 = 270 O 1 30 D 1 20 O 2 40 D 2

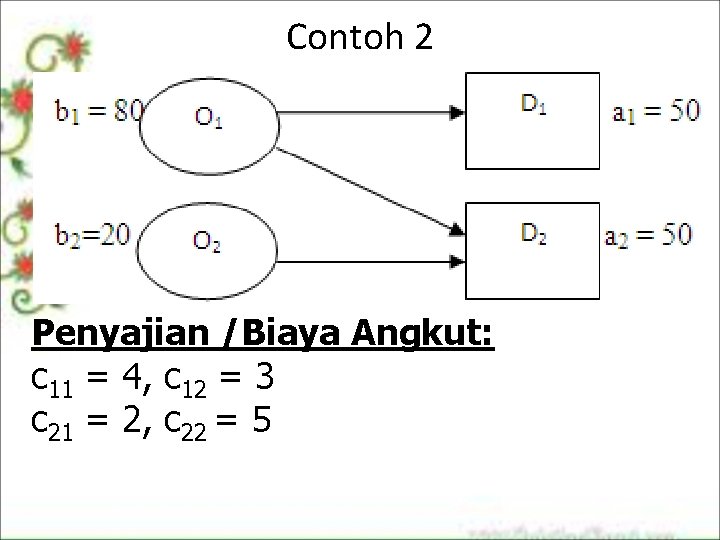
Contoh 2 Penyajian /Biaya Angkut: c 11 = 4, c 12 = 3 c 21 = 2, c 22 = 5

Tabel awal diisi dengan metode North-West-Corner Langkah 1: Menyusun Tabel • Setiap pengisian harus full kolom/ baris 50 30 20

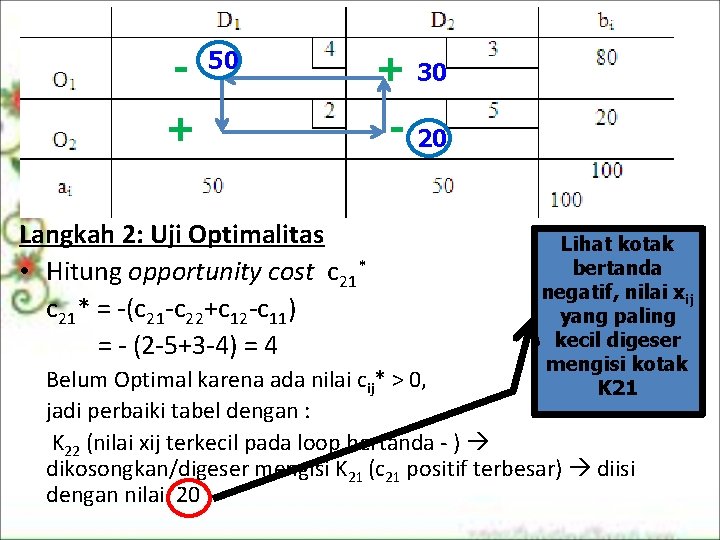
- 50 + Langkah 2: Uji Optimalitas • Hitung opportunity cost c 21* = (c 21 c 22+c 12 c 11) = (2 5+3 4) = 4 + 30 - 20 Lihat kotak bertanda negatif, nilai xij yang paling kecil digeser mengisi kotak K 21 Belum Optimal karena ada nilai cij* > 0, jadi perbaiki tabel dengan : K 22 (nilai xij terkecil pada loop bertanda ) dikosongkan/digeser mengisi K 21 (c 21 positif terbesar) diisi dengan nilai 20

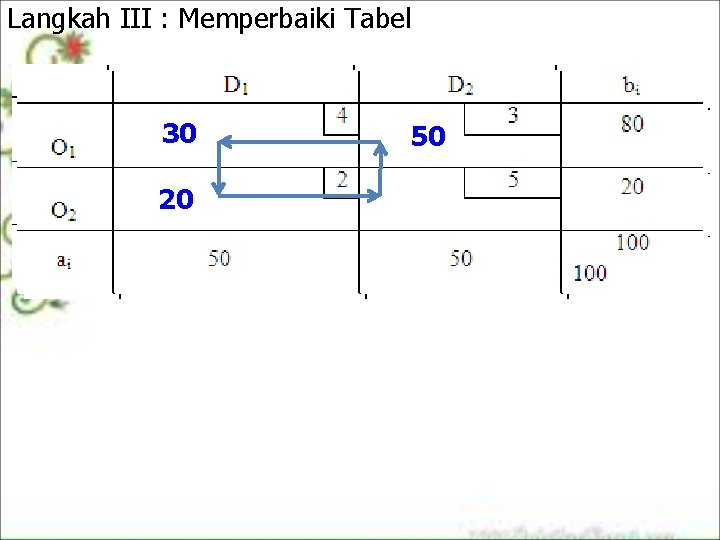
Langkah III : Memperbaiki Tabel 50 30 30 20 20 20

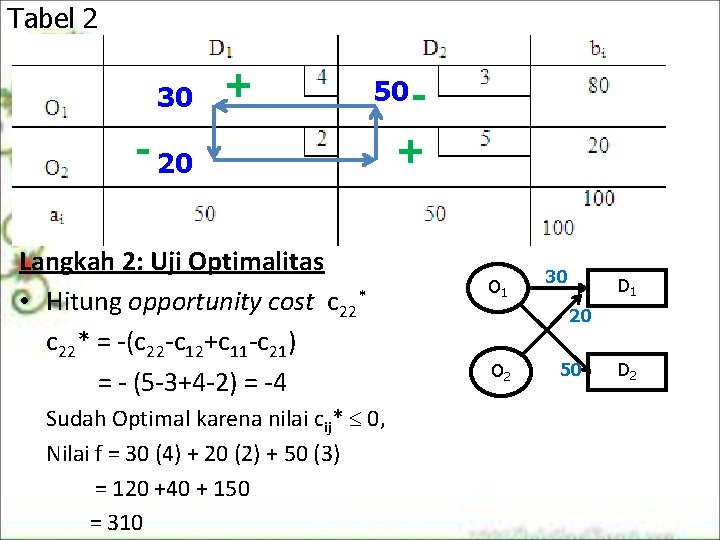
Tabel 2 30 + 50 - - 20 Langkah 2: Uji Optimalitas • Hitung opportunity cost c 22* = (c 22 c 12+c 11 c 21) = (5 3+4 2) = 4 Sudah Optimal karena nilai cij* 0, Nilai f = 30 (4) + 20 (2) + 50 (3) = 120 +40 + 150 = 310 + O 1 30 D 1 20 O 2 50 D 2

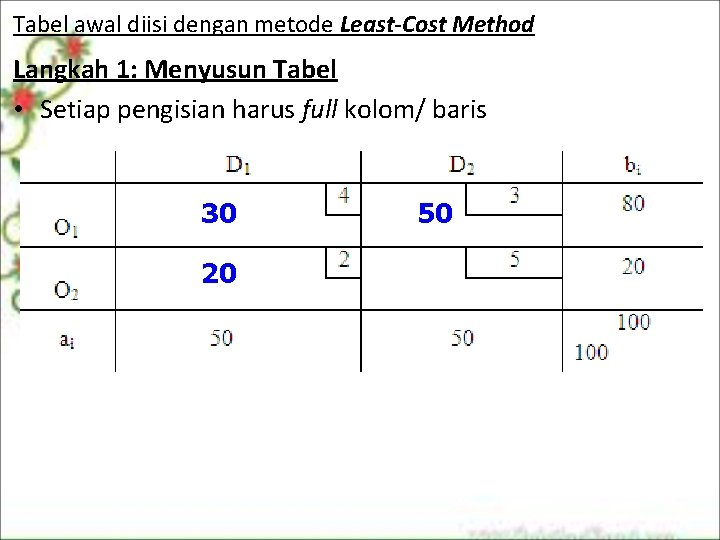
Tabel awal diisi dengan metode Least-Cost Method Langkah 1: Menyusun Tabel • Setiap pengisian harus full kolom/ baris 30 20 50

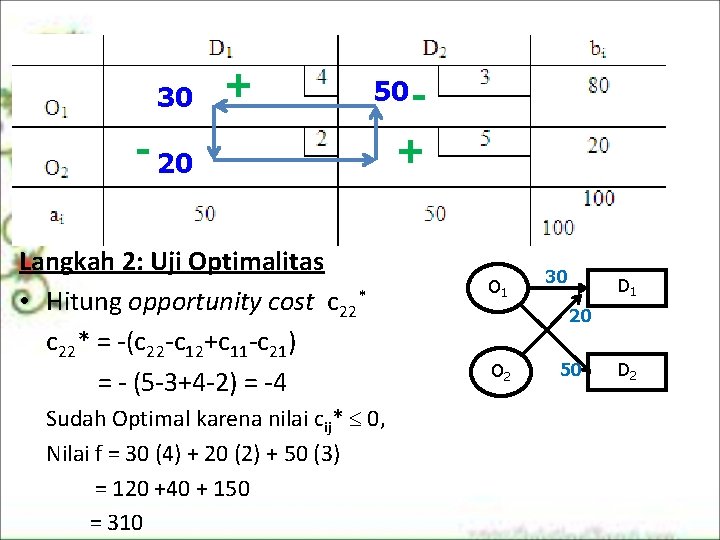
30 + 50 - - 20 Langkah 2: Uji Optimalitas • Hitung opportunity cost c 22* = (c 22 c 12+c 11 c 21) = (5 3+4 2) = 4 Sudah Optimal karena nilai cij* 0, Nilai f = 30 (4) + 20 (2) + 50 (3) = 120 +40 + 150 = 310 + O 1 30 D 1 20 O 2 50 D 2

Contoh 3 • Suatu perusahaan mempunyai 4 buah pabrik dengan 4 daerah pemasaran. Ke empat pabrik mempunyai kapasitas produksi yang sama yaitu 100 ton. Sedangkan ke empat daerah pemasaran masing mempunyai demand 75, 160 dan 90 ton per bulan. Tentukan besarnya komoditi yang seharusnya diikirim dari masing pabrik ke masing daerah pemasaran agar ongkos angkut total minimal, jika diketahui ongkos angkut satuan dari setiap pabrik ke daerah pemasaran sebagai berikut:

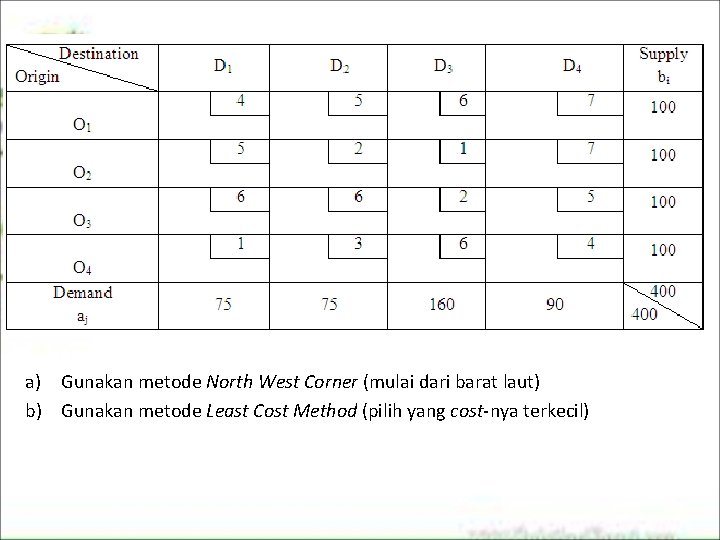
a) Gunakan metode North West Corner (mulai dari barat laut) b) Gunakan metode Least Cost Method (pilih yang cost nya terkecil)

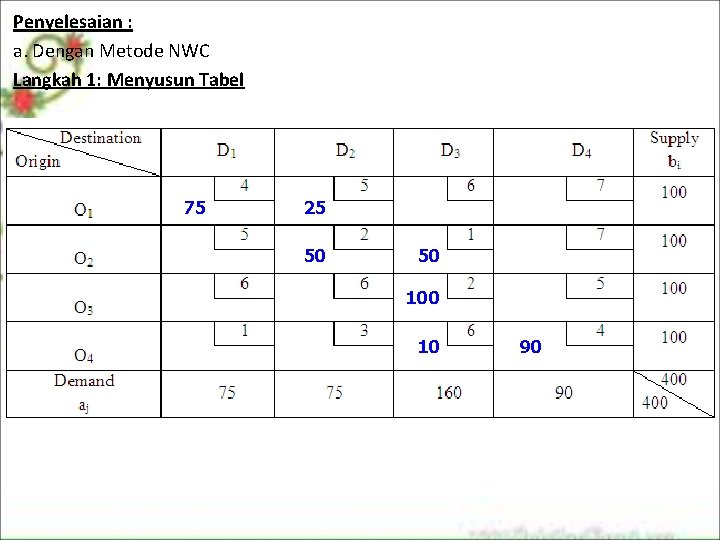
Penyelesaian : a. Dengan Metode NWC Langkah 1: Menyusun Tabel 75 25 50 50 10 90

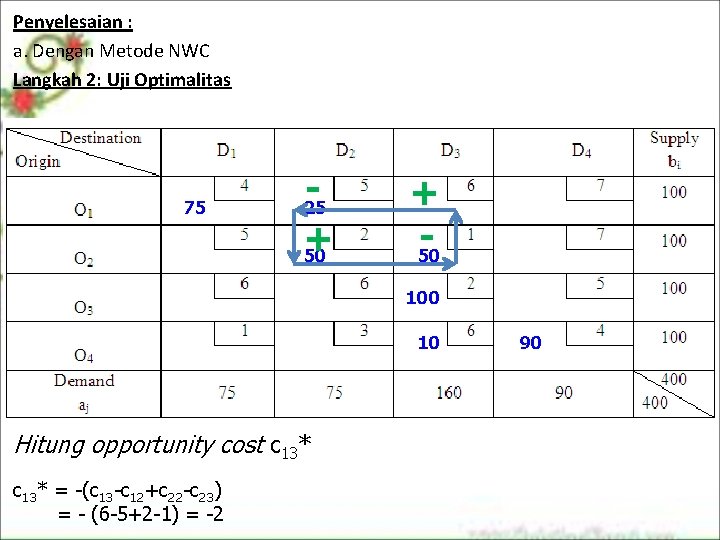
Penyelesaian : a. Dengan Metode NWC Langkah 2: Uji Optimalitas 75 + 50 25 + 50 10 Hitung opportunity cost c 13* = -(c 13 -c 12+c 22 -c 23) = - (6 -5+2 -1) = -2 90

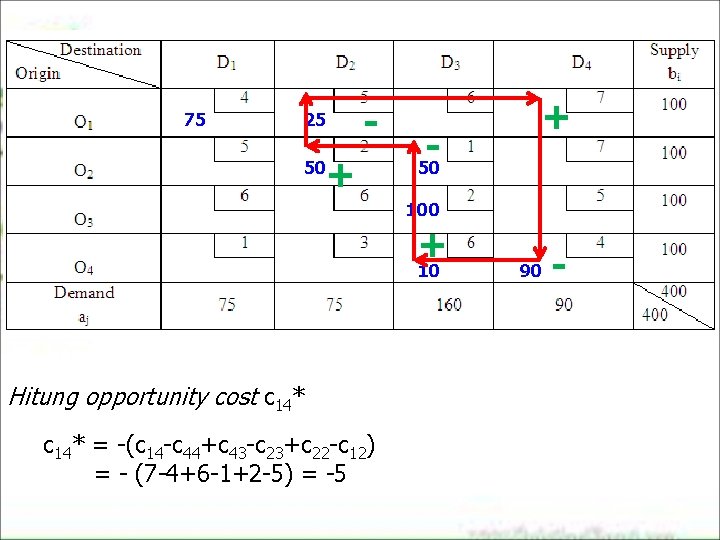
75 25 - + 50 50 + 10 Hitung opportunity cost c 14* = -(c 14 -c 44+c 43 -c 23+c 22 -c 12) = - (7 -4+6 -1+2 -5) = -5 90 -

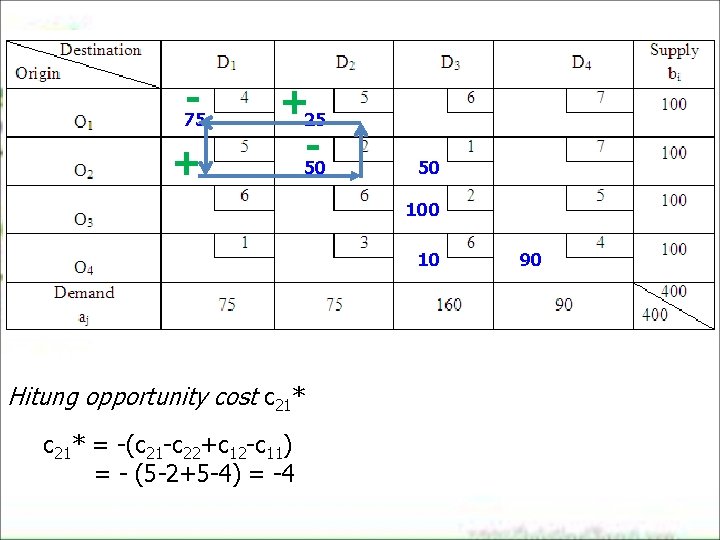
-75 + +25 -50 50 10 Hitung opportunity cost c 21* = -(c 21 -c 22+c 12 -c 11) = - (5 -2+5 -4) = -4 90

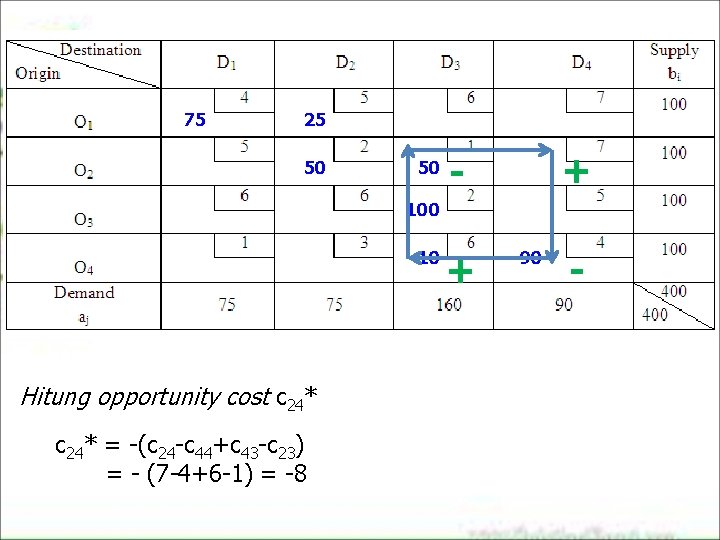
75 25 50 50 + - 100 10 Hitung opportunity cost c 24* = -(c 24 -c 44+c 43 -c 23) = - (7 -4+6 -1) = -8 + 90 -

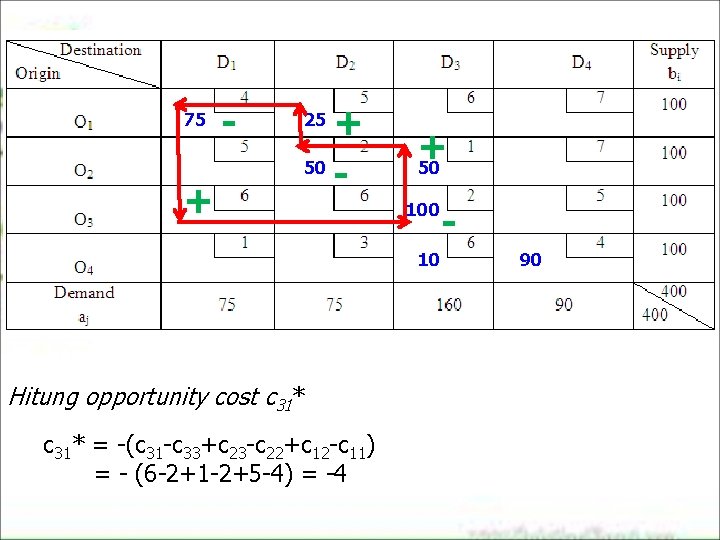
75 + - + 50 25 + 50 10 Hitung opportunity cost c 31* = -(c 31 -c 33+c 23 -c 22+c 12 -c 11) = - (6 -2+1 -2+5 -4) = -4 90

75 25 -50 + 50 10 Hitung opportunity cost c 32* = -(c 32 -c 33+c 23 -c 22) = - (6 -2+1 -2) = -3 + 90

75 25 50 50 10 + 100 Hitung opportunity cost c 34* = -(c 34 -c 44+c 43 -c 33) = - (5 -4+6 -2) = -5 + 90 -

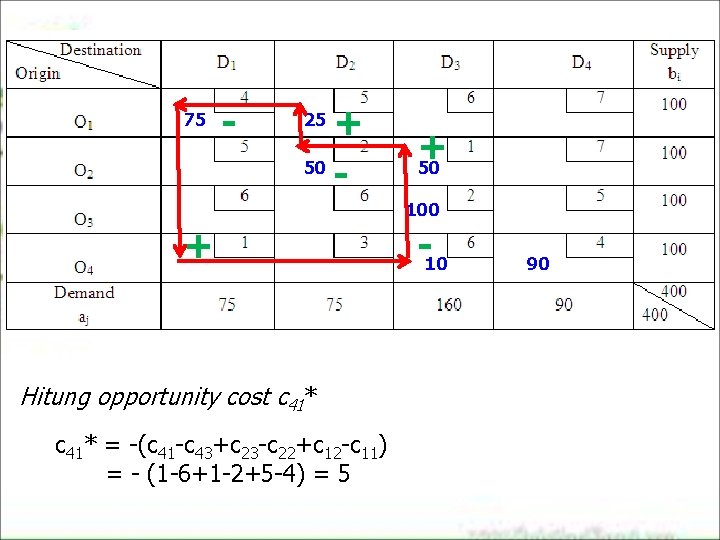
75 - + 50 25 + 50 100 + Hitung opportunity cost c 41* = -(c 41 -c 43+c 23 -c 22+c 12 -c 11) = - (1 -6+1 -2+5 -4) = 5 -10 90

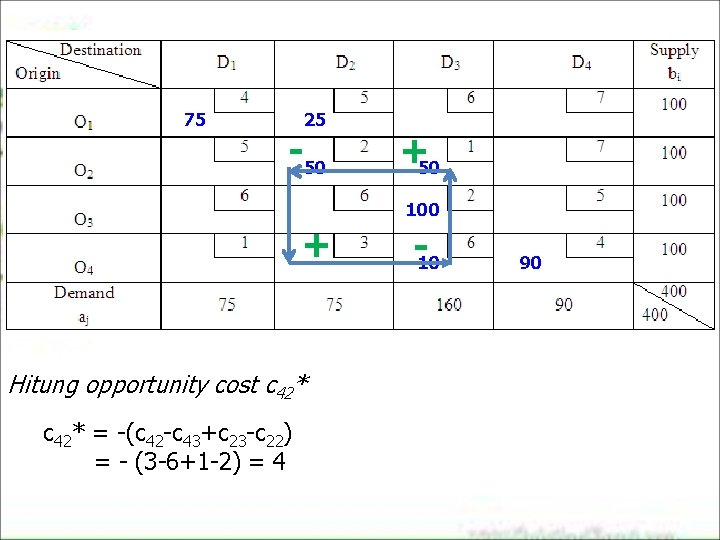
75 25 -50 +50 100 + Hitung opportunity cost c 42* = -(c 42 -c 43+c 23 -c 22) = - (3 -6+1 -2) = 4 -10 90

Langkah 2: Uji Optimalitas; Hitung opportunity cost cij* c 13* = (c 13 c 12+c 22 c 23) = (6 5+2 1) = 2 c 14* = (c 14 c 44+c 43 c 23+c 22 c 12) = (7 4+6 1+2 5) = 5 c 21* = (c 21 c 22+c 12 c 11) = (5 2+5 4) = 4 c 24* = (c 24 c 44+c 43 c 23) = (7 4+6 1) = 8 c 31* = -(c 31 -c 33+c 23 -c 22+c 12 -c 11) = - (6 -2+1 -2+5 -4) = -4 c 32* = -(c 32 -c 33+c 23 -c 22) = - (6 -2+1 -2) = -3 c 34* = -(c 34 -c 44+c 43 -c 33) = - (5 -4+6 -2) = -5 c 41* = -(c 41 -c 43+c 23 -c 22+c 12 -c 11) = - (1 -6+1 -2+5 -4) = 5 c 42* = -(c 42 -c 43+c 23 -c 22) = - (3 -6+1 -2) = 4 Belum Optimal karena ada nilai cij* > 0, jadi perbaiki tabel. Perhatikan karena nilai c 41* = 5, positif terbesar, maka k 41 adalah kotak yang akan diisi.

Langkah 3 : Memperbaiki Tabel Cara memperbaiki tabel • Lihat nilai cij* positif terbesar (jika ada yang sama pilih salah satu) Karena c 41* yang terbesar, maka K 41 menjadi kotak yang harus diisi dengan nilai komoditi paling melarat yang diambil dari nilai terkecil dalam loop bertanda negatif ( ) pada loop c 41* • Nilai komoditi paling melarat, dilihat pada loop untuk c 41*, lihat nilai komoditi pada kotak yang bertanda negatif ( ), nilai yang terkecil menjadi nilai yang paling melarat, yaitu nilai komoditi 10 yang berada pada K 43 dan menjadi nilai komoditi yang harus digeser ke kotak K 41 ; Kotak K 43 dikosongkan. • Perbaikan nilai komoditi, dilakukan dengan penyesuaian nilai komoditi pada nilai komoditi yang berada dalam loop c 41*.

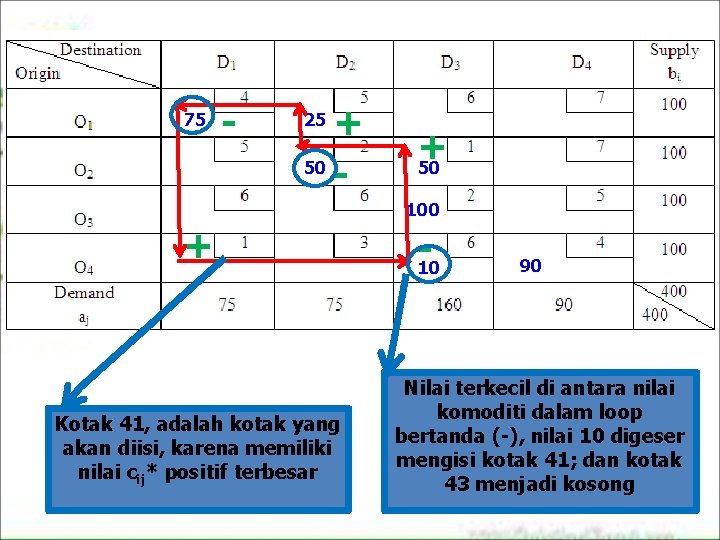
75 - + 50 25 + 50 100 + Kotak 41, adalah kotak yang akan diisi, karena memiliki nilai cij* positif terbesar -10 90 Nilai terkecil di antara nilai komoditi dalam loop bertanda (-), nilai 10 digeser mengisi kotak 41; dan kotak 43 menjadi kosong

Perbaikan nilai komoditi, dilakukan dengan penyesuaian nilai komoditi pada nilai-nilai komoditi yang berada dalam loop c 41*. 75 65 75 25 35 25 50 40 50 50 60 50 100 10 10 90 90 90

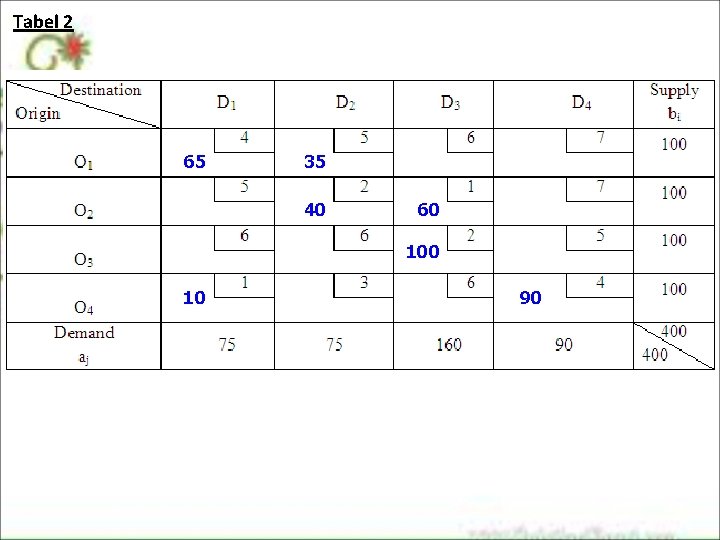
Tabel 2 65 35 40 60 10 90

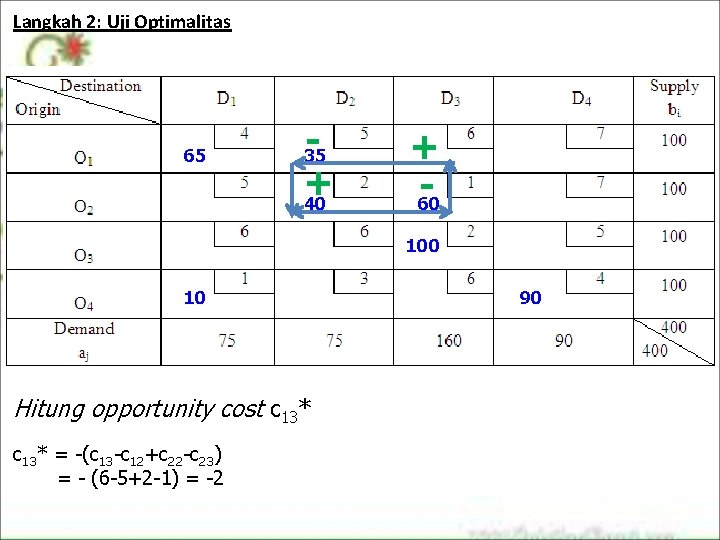
Langkah 2: Uji Optimalitas 65 + 40 35 + 60 10 Hitung opportunity cost c 13* = -(c 13 -c 12+c 22 -c 23) = - (6 -5+2 -1) = -2 90

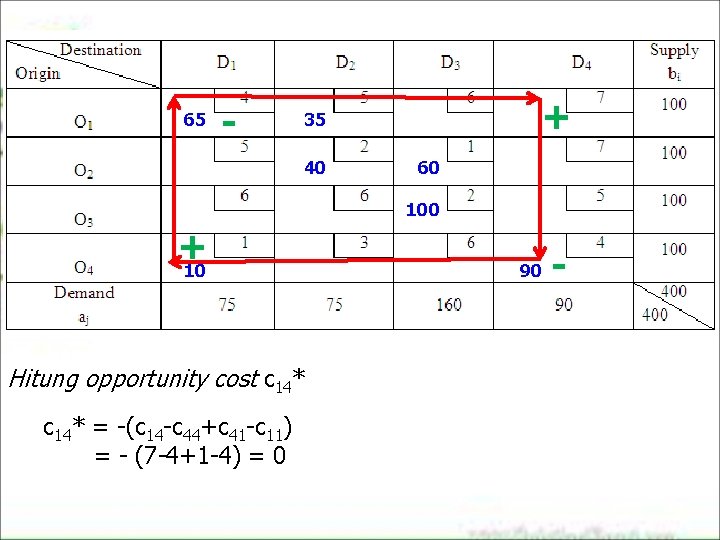
65 - + 35 40 60 100 + 10 Hitung opportunity cost c 14* = -(c 14 -c 44+c 41 -c 11) = - (7 -4+1 -4) = 0 90 -

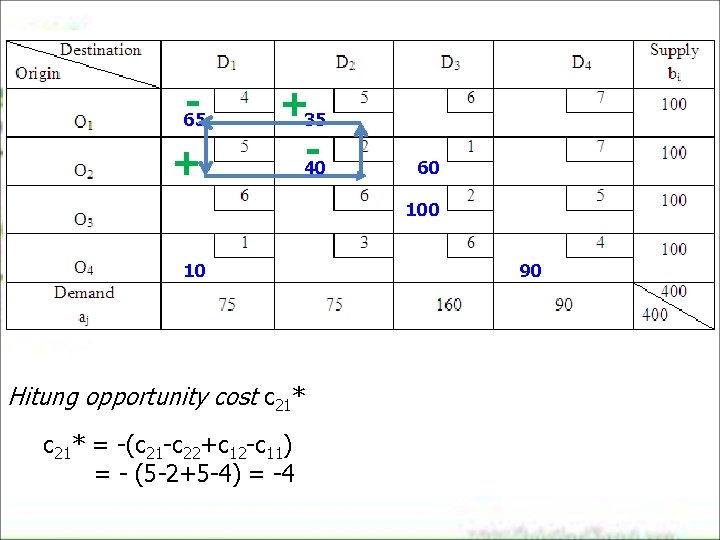
- 65 + +35 40 60 10 Hitung opportunity cost c 21* = -(c 21 -c 22+c 12 -c 11) = - (5 -2+5 -4) = -4 90

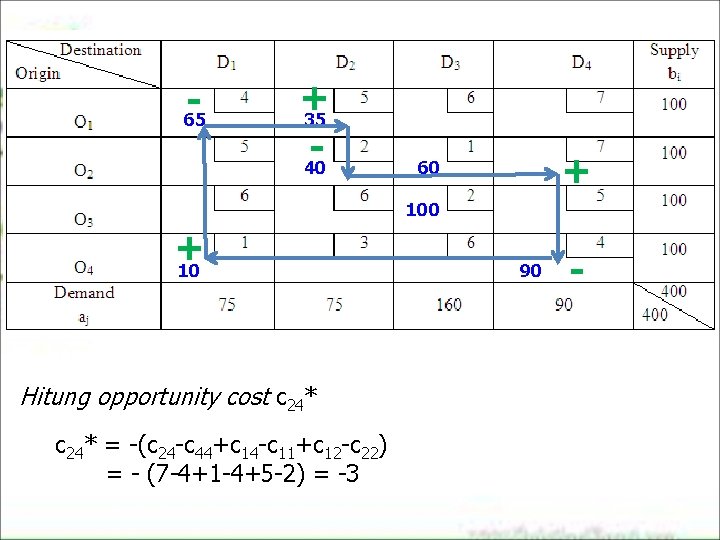
65 + 35 40 + 60 100 + 10 Hitung opportunity cost c 24* = -(c 24 -c 44+c 14 -c 11+c 12 -c 22) = - (7 -4+1 -4+5 -2) = -3 90 -

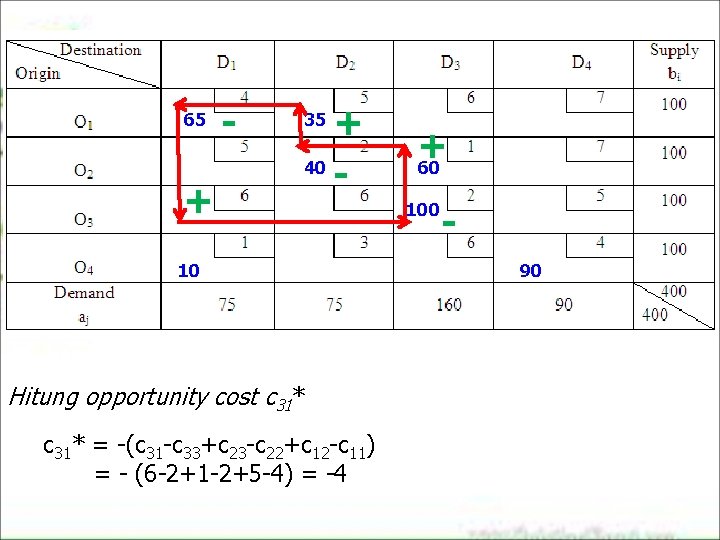
65 + - + 40 35 10 Hitung opportunity cost c 31* = -(c 31 -c 33+c 23 -c 22+c 12 -c 11) = - (6 -2+1 -2+5 -4) = -4 + 60 100 90

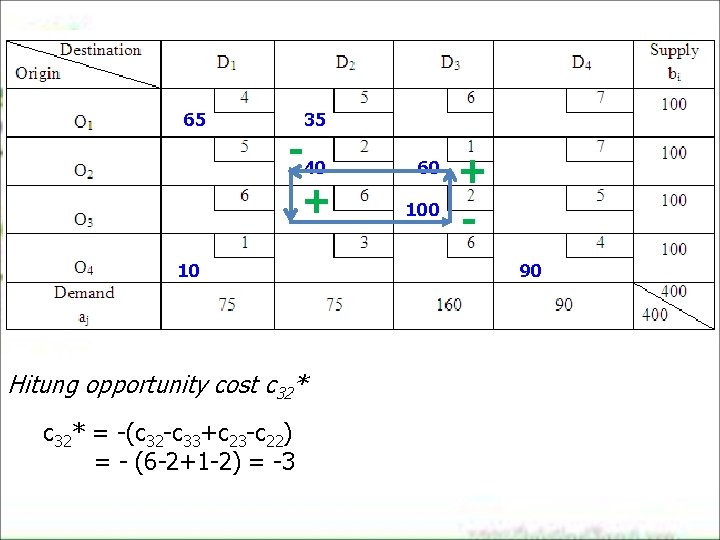
65 35 -40 + 10 Hitung opportunity cost c 32* = -(c 32 -c 33+c 23 -c 22) = - (6 -2+1 -2) = -3 60 100 + 90

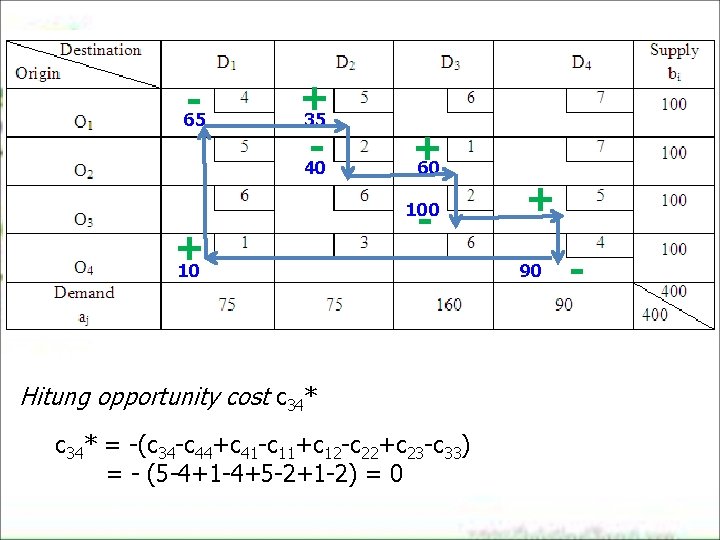
65 + 35 40 + 60 - 100 + 10 Hitung opportunity cost c 34* = -(c 34 -c 44+c 41 -c 11+c 12 -c 22+c 23 -c 33) = - (5 -4+1 -4+5 -2+1 -2) = 0 + 90 -

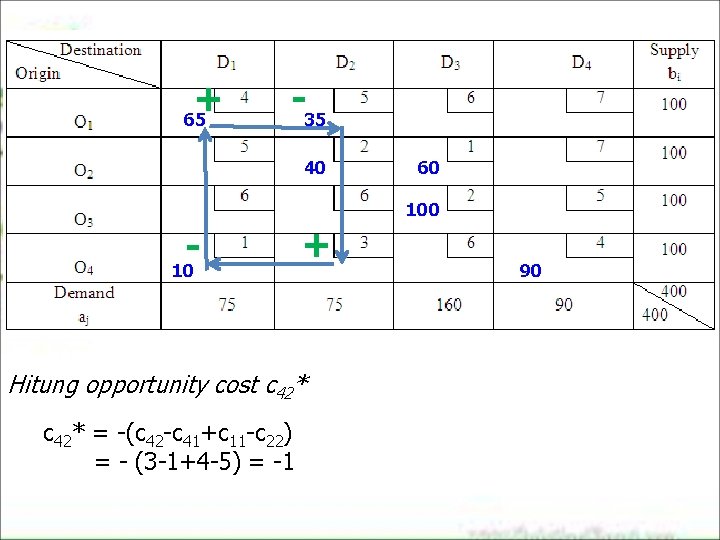
+ 65 -35 40 60 100 - 10 + Hitung opportunity cost c 42* = -(c 42 -c 41+c 11 -c 22) = - (3 -1+4 -5) = -1 90

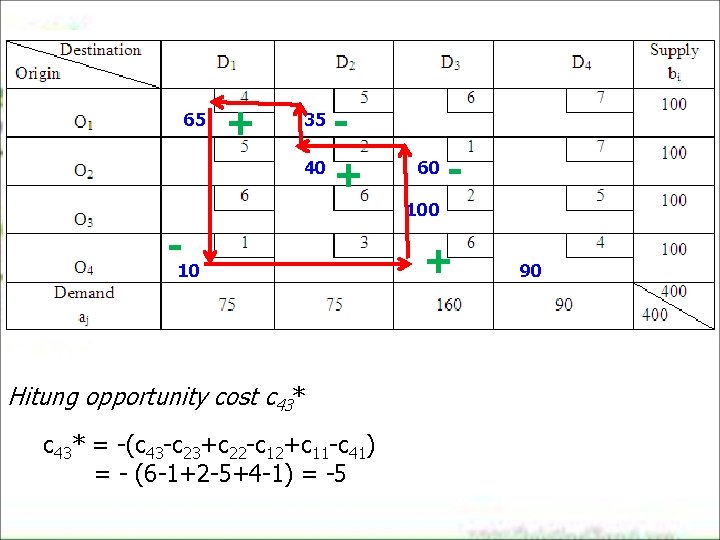
65 + 40 + 35 60 - 10 Hitung opportunity cost c 43* = -(c 43 -c 23+c 22 -c 12+c 11 -c 41) = - (6 -1+2 -5+4 -1) = -5 + 90

Langkah 2: Uji Optimalitas; Hitung opportunity cost cij* c 13* = (c 13 c 12+c 22 c 23) = (6 5+2 1) = 2 c 14* = (c 14 c 44+c 41 c 11) = (7 4+1 4) = 0 c 21* = (c 21 c 22+c 12 c 11) = (5 2+5 4) = 4 c 24* = (c 24 c 44+c 14 c 11+c 12 c 22) = (7 4+1 4+5 2) = 3 c 31* = -(c 31 -c 33+c 23 -c 22+c 12 -c 11) = - (6 -2+1 -2+5 -4) = -4 c 32* = -(c 32 -c 33+c 23 -c 22) = - (6 -2+1 -2) = -3 c 34* = -(c 34 -c 44+c 41 -c 11+c 12 c 22+c 23 -c 33) = - (5 -4+1 -4+5 -2+1 -2)= 0 c 42* = -(c 42 -c 41+c 11 -c 22) = - (3 -1+4 -5) = -1 c 43* = -(c 43 -c 23+c 22 -c 12+c 11 -c 41) = - (6 -1+2 -5+4 -1) = -5 Tabel 2 sudah Optimal karena semua nilai cij* ≤ 0 , dengan nilai foptimal = 65(4) + 35(5) + 40(2) + 60(1) + 100(2) +10(1)+90(4) = 260 + 175 +80 + 60 + 200 + 10 + 360 = 1145

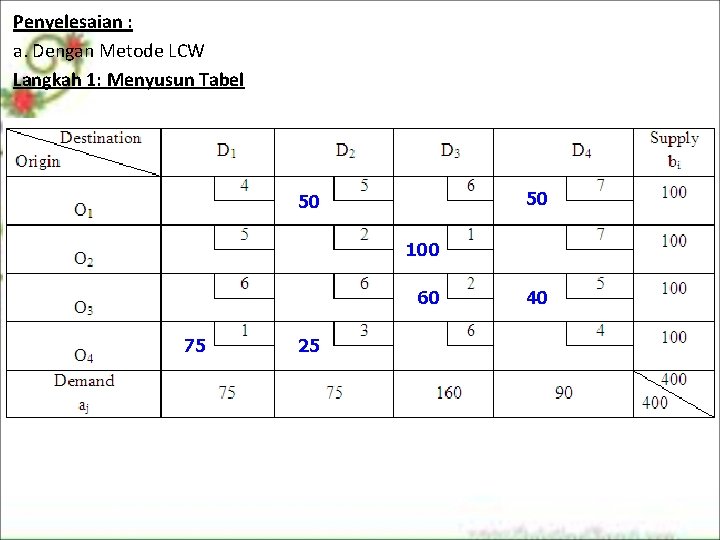
Penyelesaian : a. Dengan Metode LCW Langkah 1: Menyusun Tabel 50 50 100 60 75 25 40

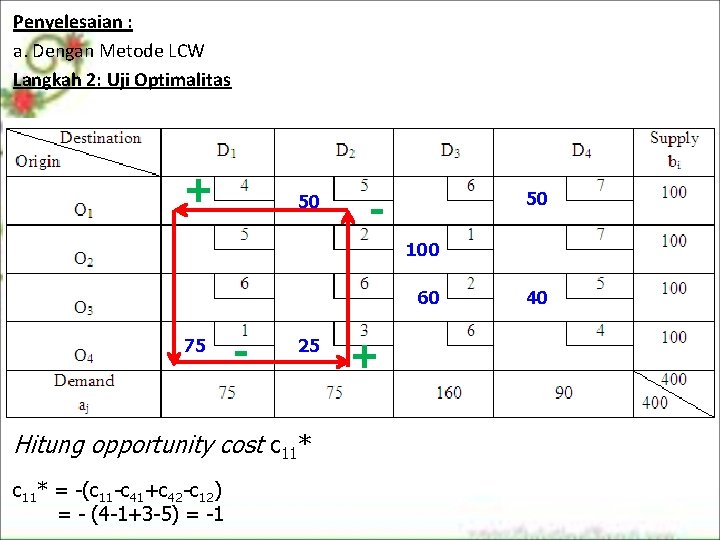
Penyelesaian : a. Dengan Metode LCW Langkah 2: Uji Optimalitas + 50 - 50 100 60 75 - 25 Hitung opportunity cost c 11* = -(c 11 -c 41+c 42 -c 12) = - (4 -1+3 -5) = -1 + 40

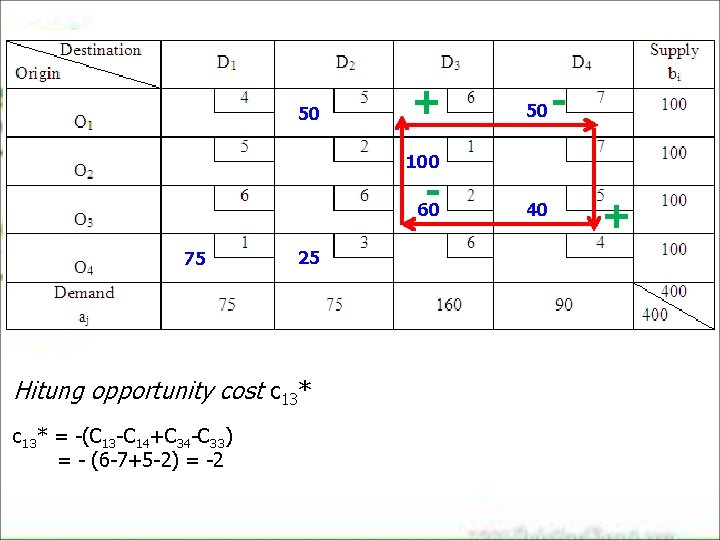
50 + 50 - 100 - 60 75 25 Hitung opportunity cost c 13* = -(C 13 -C 14+C 34 -C 33) = - (6 -7+5 -2) = -2 40 +

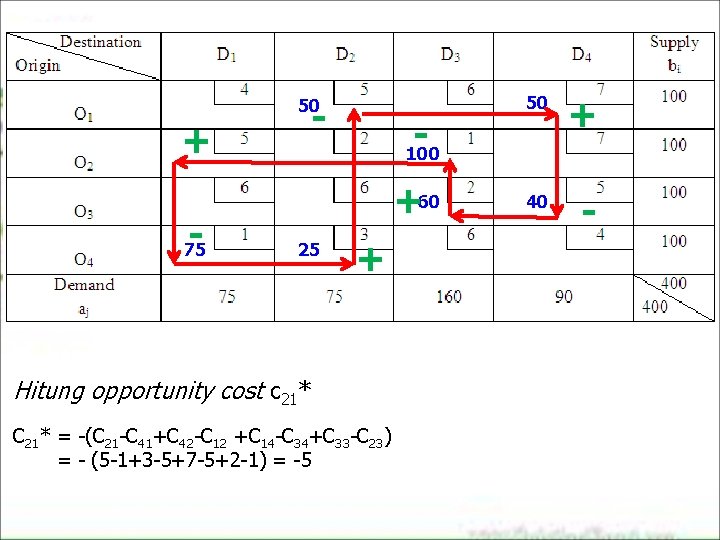
50 - + - 75 - 50 + 40 - 100 +60 25 + Hitung opportunity cost c 21* C 21* = -(C 21 -C 41+C 42 -C 12 +C 14 -C 34+C 33 -C 23) = - (5 -1+3 -5+7 -5+2 -1) = -5

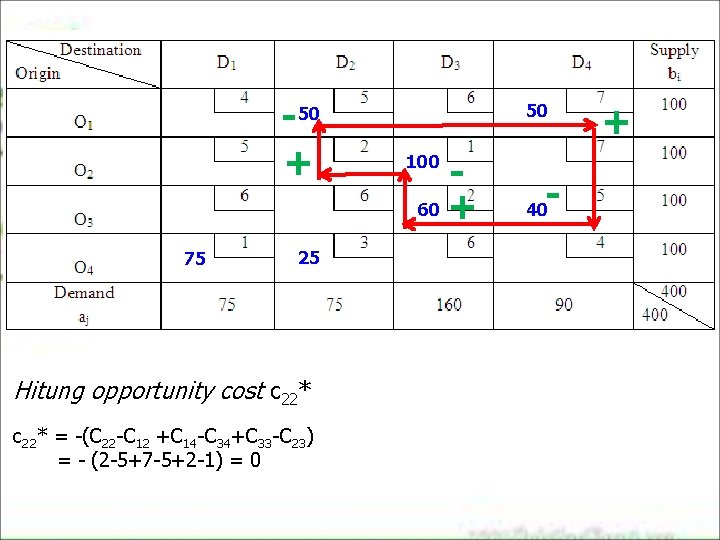
-50 + 75 25 Hitung opportunity cost c 22* = -(C 22 -C 12 +C 14 -C 34+C 33 -C 23) = - (2 -5+7 -5+2 -1) = 0 50 60 + 100 - 40 +

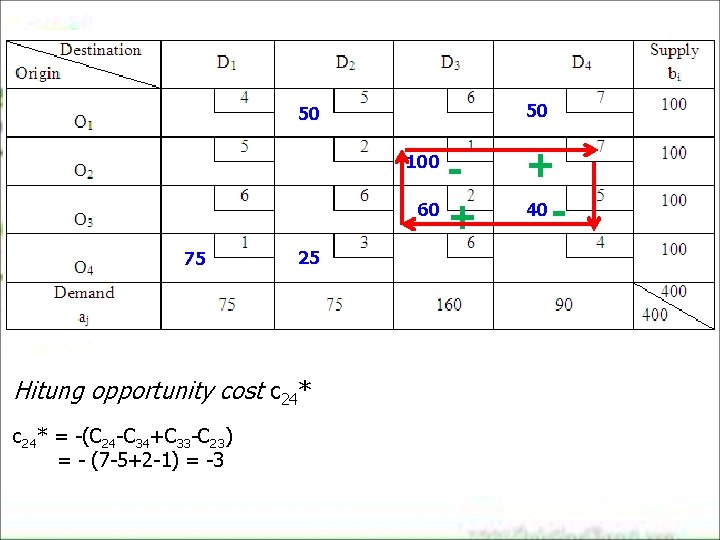
50 50 60 + 100 75 25 Hitung opportunity cost c 24* = -(C 24 -C 34+C 33 -C 23) = - (7 -5+2 -1) = -3 + 40 -

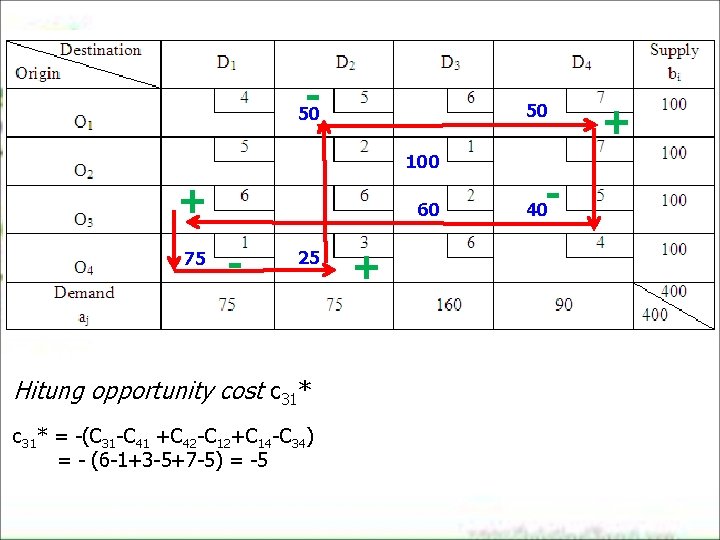
- 50 50 100 + 75 60 - 25 Hitung opportunity cost c 31* = -(C 31 -C 41 +C 42 -C 12+C 14 -C 34) = - (6 -1+3 -5+7 -5) = -5 + - 40 +

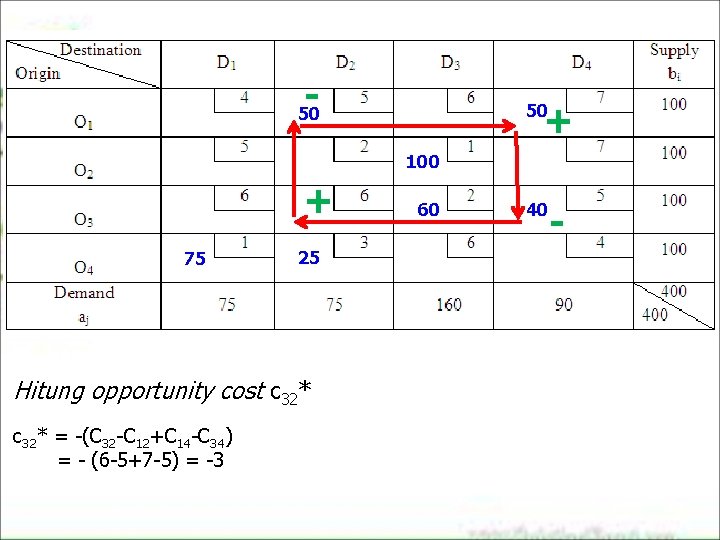
- + 50 50 100 + 75 25 Hitung opportunity cost c 32* = -(C 32 -C 12+C 14 -C 34) = - (6 -5+7 -5) = -3 60 40 -

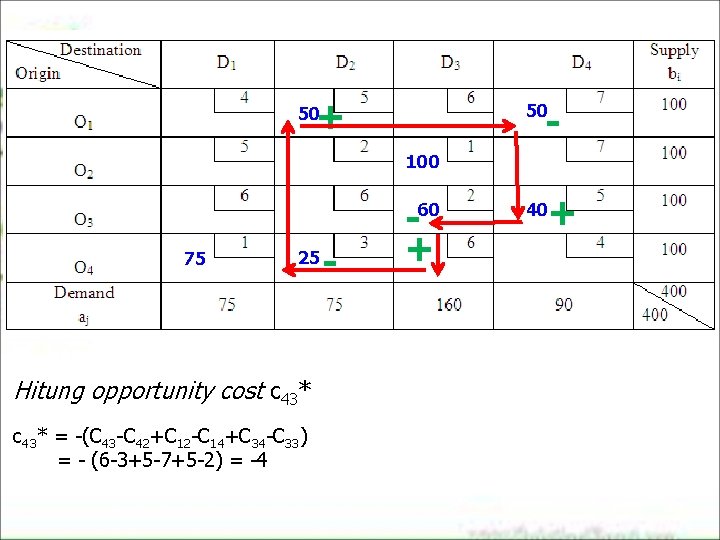
+ 50 - 50 100 + 60 75 25 Hitung opportunity cost c 43* = -(C 43 -C 42+C 12 -C 14+C 34 -C 33) = - (6 -3+5 -7+5 -2) = -4 - + 40

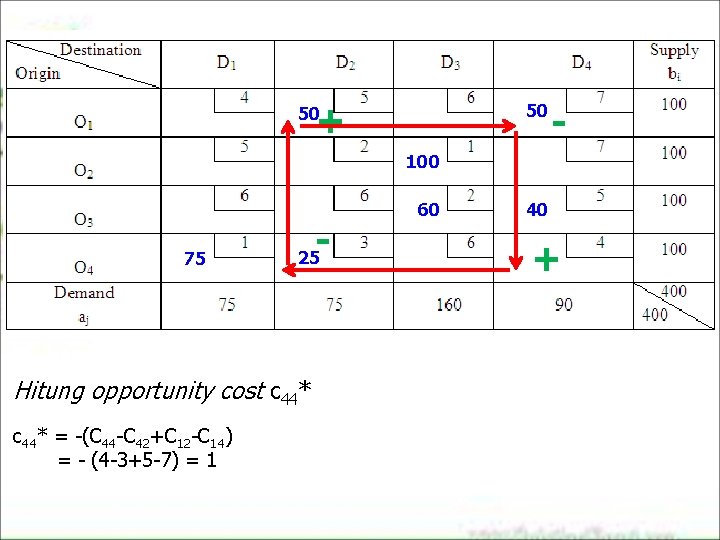
+ 50 50 - 100 75 Hitung opportunity cost c 44* = -(C 44 -C 42+C 12 -C 14) = - (4 -3+5 -7) = 1 - 25 60 40 +

Langkah 2: Uji Optimalitas; Hitung opportunity cost cij* c 11* = (C 11 C 41+C 42 C 12) = (4 1+3 5) = 1 c 13* = (C 13 C 14+C 34 C 33) = (6 7+5 2) = 2 c 21* = (C 21 C 41+C 42 C 12 +C 14 C 34+C 33 C 23) = (5 1+3 5+7 5+2 1)= 5 c 22*= (C 22 C 12+C 14 C 34+C 33 C 23) = (2 5+7 5+2 1) = 0 c 24* = -(C 24 -C 34+C 33 -C 23) = - (7 -5+2 -1) = -3 c 31*= -(c 31 -c 41+c 42 -c 12+c 14 -c 34) = - (6 -1+3 -5+7 -5) = -5 c 32* = -(C 32 -C 12+C 14 -C 34) = - (6 -5+7 -5) = -3 c 43* = -(c 43 -c 42+c 12 -c 14+c 34 -c 33) - (6 -3+5 -7+5 -2) = -4 c 44* = -(C 44 -C 42+C 12 -C 14) = - (4 -3+5 -7) = 1 Belum Optimal karena ada nilai cij* > 0, jadi perbaiki tabel. Perhatikan karena nilai c 44* = 1, positif, maka k 44 adalah kotak yang akan diisi.

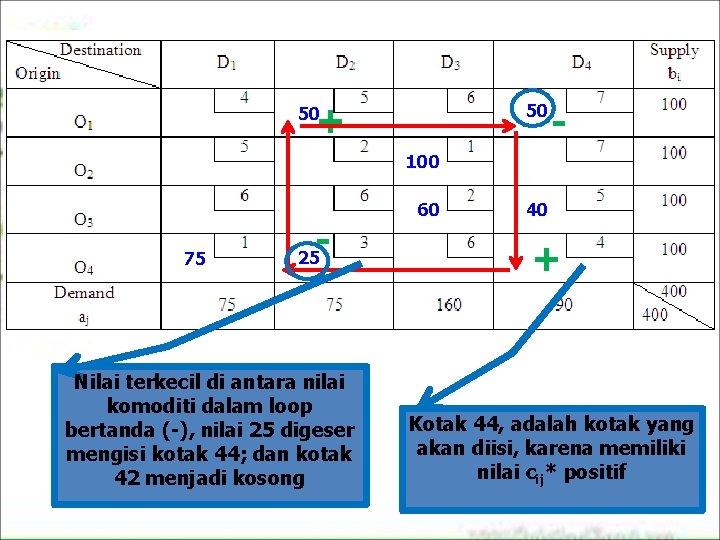
+ 50 50 - 100 75 - 25 Nilai terkecil di antara nilai komoditi dalam loop bertanda (-), nilai 25 digeser mengisi kotak 44; dan kotak 42 menjadi kosong 60 40 + Kotak 44, adalah kotak yang akan diisi, karena memiliki nilai cij* positif

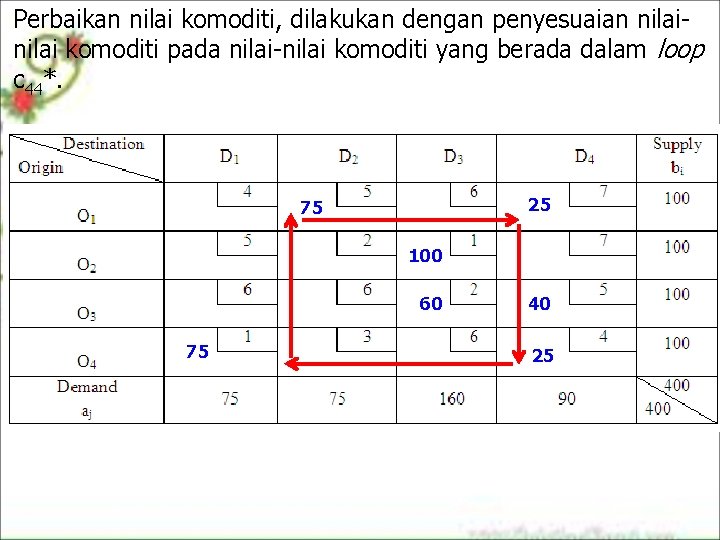
Perbaikan nilai komoditi, dilakukan dengan penyesuaian nilai komoditi pada nilai-nilai komoditi yang berada dalam loop c 44*. 50 50 25 50 50 75 100 60 60 75 75 25 40 40 25

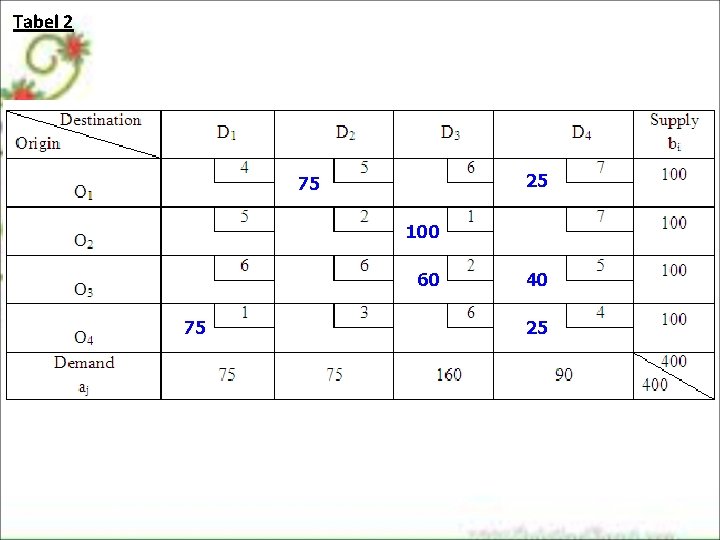
Tabel 2 25 75 100 60 75 40 25

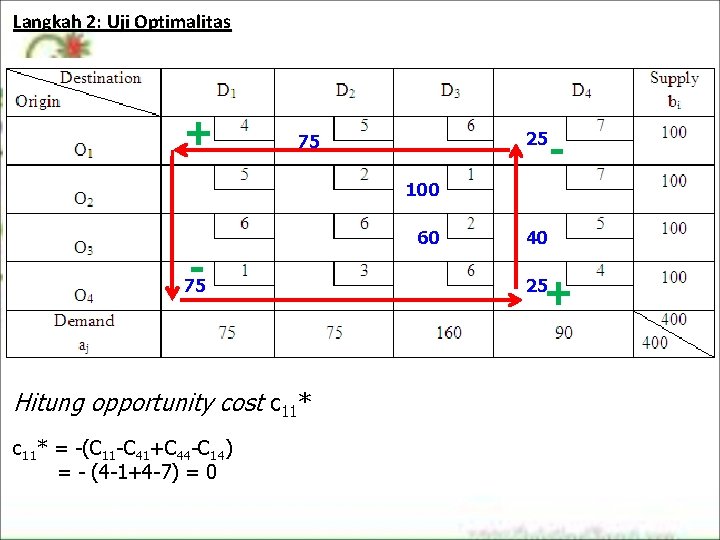
Langkah 2: Uji Optimalitas + 25 75 - 100 - 75 Hitung opportunity cost c 11* = -(C 11 -C 41+C 44 -C 14) = - (4 -1+4 -7) = 0 60 40 + 25

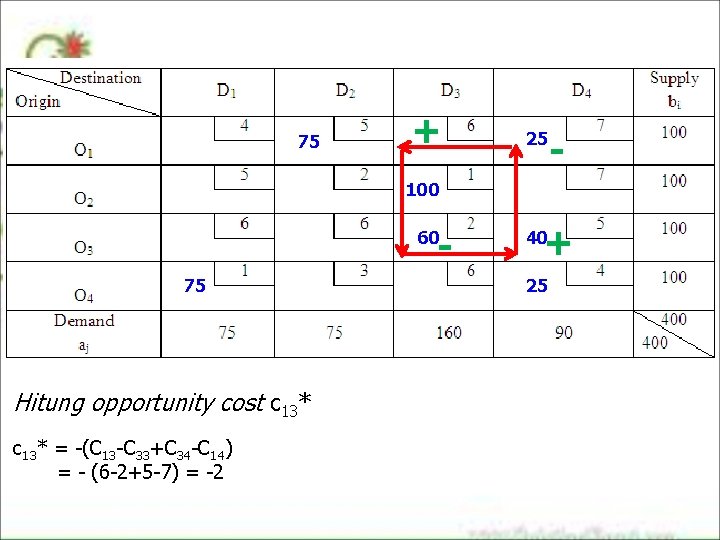
75 + 25 - 100 - 60 75 Hitung opportunity cost c 13* = -(C 13 -C 33+C 34 -C 14) = - (6 -2+5 -7) = -2 + 40 25

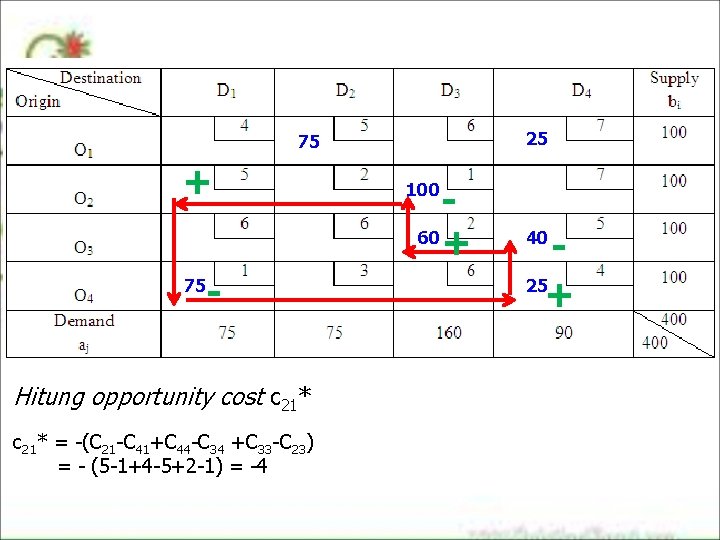
25 75 + - 75 Hitung opportunity cost c 21* = -(C 21 -C 41+C 44 -C 34 +C 33 -C 23) = - (5 -1+4 -5+2 -1) = -4 60 + 100 25 + 40

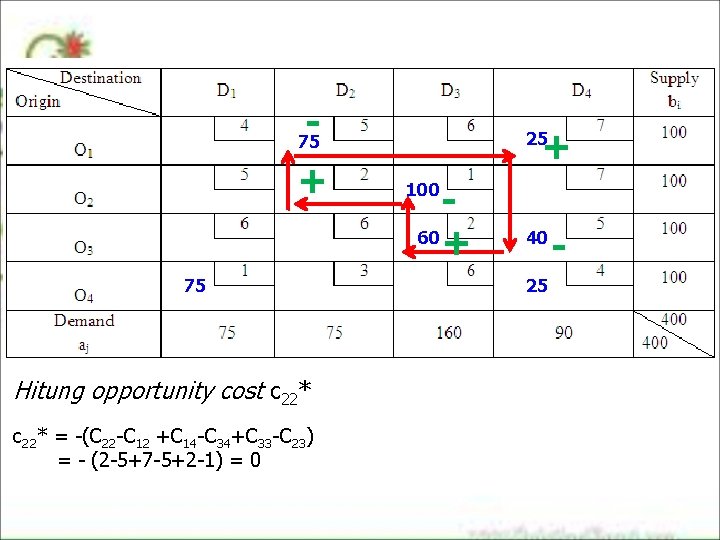
- + 25 75 + 75 Hitung opportunity cost c 22* = -(C 22 -C 12 +C 14 -C 34+C 33 -C 23) = - (2 -5+7 -5+2 -1) = 0 60 + 100 40 25 -

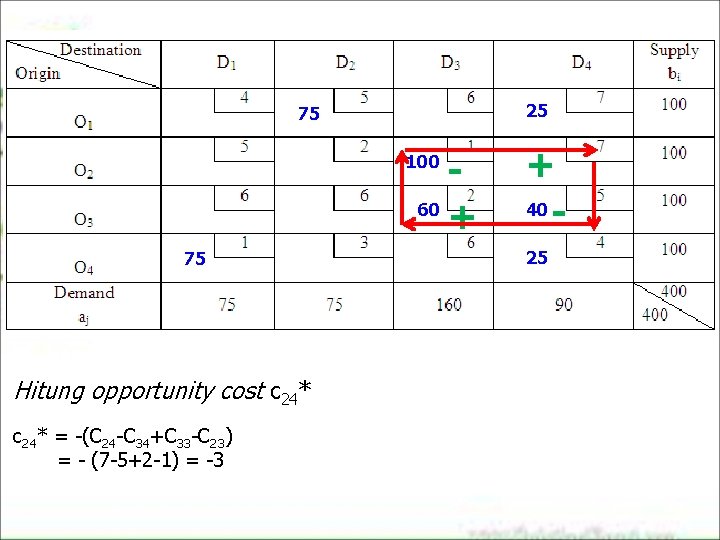
25 75 60 + 100 75 Hitung opportunity cost c 24* = -(C 24 -C 34+C 33 -C 23) = - (7 -5+2 -1) = -3 + 40 25

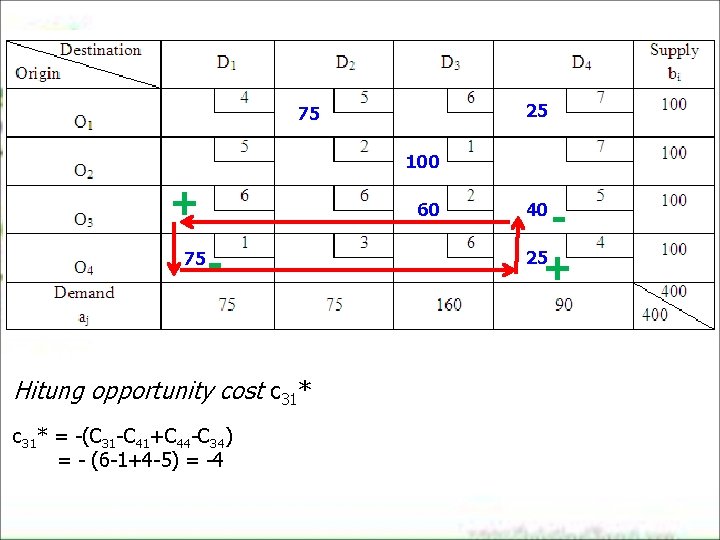
25 75 100 + 75 60 - Hitung opportunity cost c 31* = -(C 31 -C 41+C 44 -C 34) = - (6 -1+4 -5) = -4 25 + 40

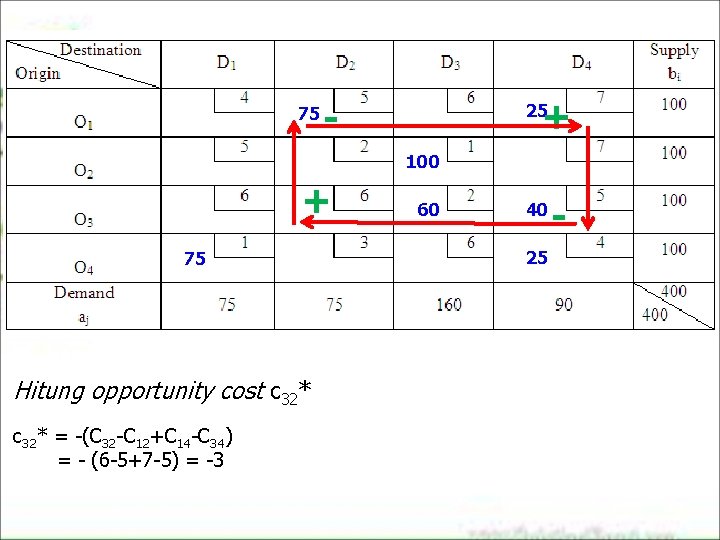
75 + - 25 100 + 75 Hitung opportunity cost c 32* = -(C 32 -C 12+C 14 -C 34) = - (6 -5+7 -5) = -3 60 40 25 -

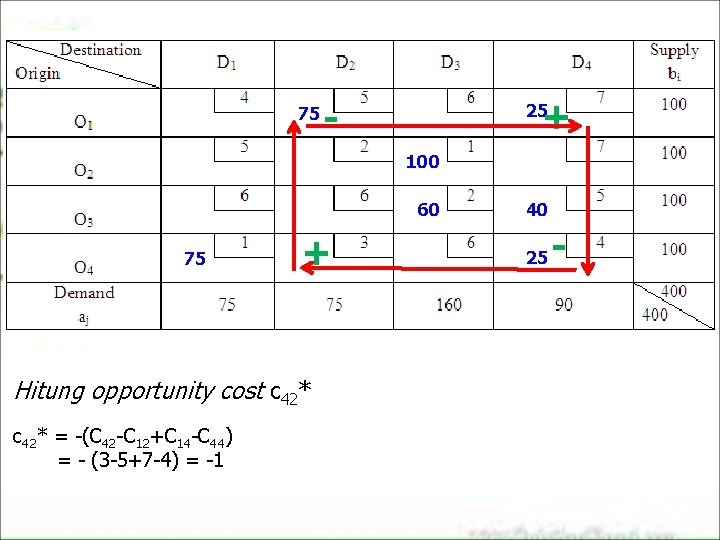
75 + - 25 100 60 75 + Hitung opportunity cost c 42* = -(C 42 -C 12+C 14 -C 44) = - (3 -5+7 -4) = -1 40 25 -

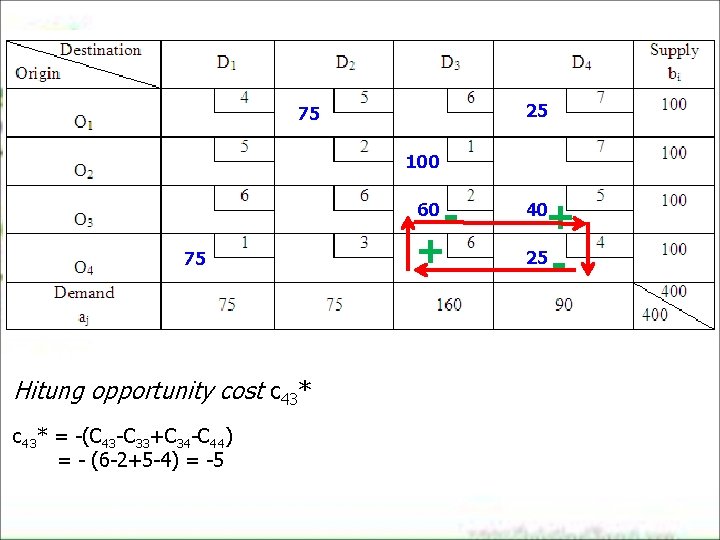
25 75 100 + 60 75 Hitung opportunity cost c 43* = -(C 43 -C 33+C 34 -C 44) = - (6 -2+5 -4) = -5 + 25 40

Langkah 2: Uji Optimalitas; Hitung opportunity cost cij* c 11* = (C 11 C 41+C 44 C 14) = (4 1+4 7) = 0 c 13* = (C 13 C 33+C 34 C 14) c 24* = -(C 24 -C 34+C 33 -C 23) = - (7 -5+2 -1) = -3 c 31*= -(C 31 -C 41+C 44 -C 34) = - (6 -1+4 -5) = -4 = (6 2+5 7) = 2 c 32* = -(C 32 -C 12+C 14 -C 34) c 21* = (c 21 c 41+c 44 c 34+c 33 c 23) = - (6 -5+7 -5) = -3 = (5 1+4 5+2 1) = 4 c 42* = -(C 42 -C 12+C 14 -C 44) c 22* = (c 22 c 12+c 14 c 34+c 33 c 23) = - (3 -5+7 -4) = -1 = (2 5+7 5+2 1) = 0 c 43* = -(C 43 -C 33+C 34 -C 44) = - (6 -2+5 -4) = -5 Tabel 2 sudah Optimal karena semua nilai cij* ≤ 0 , dengan nilai foptimal = 75(5) + 25(7) + 100(1) + 60(2) + 40(5) +75(1)+25(4) = 375 + 175 +100 + 120 + 200 + 75 + 100 = 1145