Matemticas II CAPITULO I FUNCIONES CAPITULO II INTEGRALES

Matemáticas II CAPITULO I FUNCIONES CAPITULO II INTEGRALES CAPITULO III ECUACIONES DIFERENCIALES CAPITULO IV MÉTODO PARA RESOLVER UNA ECUACIÓN DIFERENCIAL

CAPITULO I Funciones 1. 1 Exponenciales y Logarítmicas 1. 2 Diferenciación de una Función Exponencial 1. 3 Diferenciación de una Función Logarítmica 1. 3. 1 Diferenciación Logarítmica

CAPITULO II Integrales 2. 1 Integral Indefinida 2. 2 Integración de Funciones Trigonométricas 2. 3 Teorema Fundamental del Cálculo 2. 4 Método de Sustitución 2. 4. 1 Sustitución para integrales definidas 2. 5 Integración por partes

CAPITULO III Ecuaciones Diferenciales 3. 1 Introducción 3. 2 Solución de una Ecuación Diferencial 3. 2. 1 Comprobación de la solución de una ED 3. 3 Obtención de una Ecuación Diferencial a partir de la solución general.

CAPITULO IV Métodos Para Resolver una ED 4. 1 Introducción 4. 1. 1 Objetivo de los métodos para la obtención de la solución general. 4. 2 Ecuaciones de Variables Separables 4. 3 Ecuaciones Homogéneas 4. 4 Ecuaciones Exactas

BIBLIOGRAFÍA Cálculo con Geometría Analítica R. E. Larson y R. P. Hostetler Mc. Graw-Hill, 2000 Cálculo con Geometría L. Leiithold Harla, 1992 Cálculo, Concepto y Contextos J. Stewart Internacional Thompson, 1999

BIBLIOGRAFÍA Ecuaciones Diferenciales E. D. Rainville Nueva Editorial Interamericana, 1987 Cálculo Frnakes Ayres Jr. , Elliot Mendelson Mc. Graw-Hill, 2001 Matemáticas Superiores para Ingeniería C. Ray Wyle Mc. Graw-Hill, 1994

C APÍTULO I Funciones

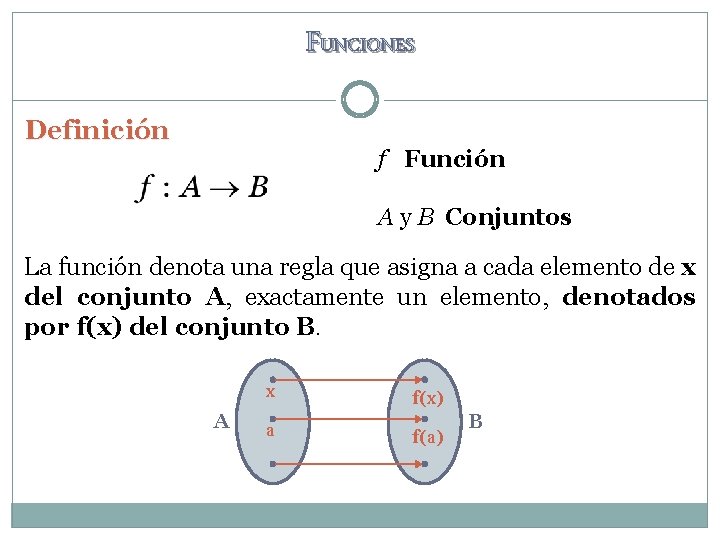
FUNCIONES Definición f Función A y B Conjuntos La función denota una regla que asigna a cada elemento de x del conjunto A, exactamente un elemento, denotados por f(x) del conjunto B. x A a f(x) f(a) B

FUNCIONES Considerando que los conjuntos A y B son conjuntos de números reales: Dominio es el conjunto A de la función, denotado por D(f). Rango es el conjunto de todos los valores posibles f(x) conforme varía en todo el dominio A. El número f(x) es el valor de f en x.

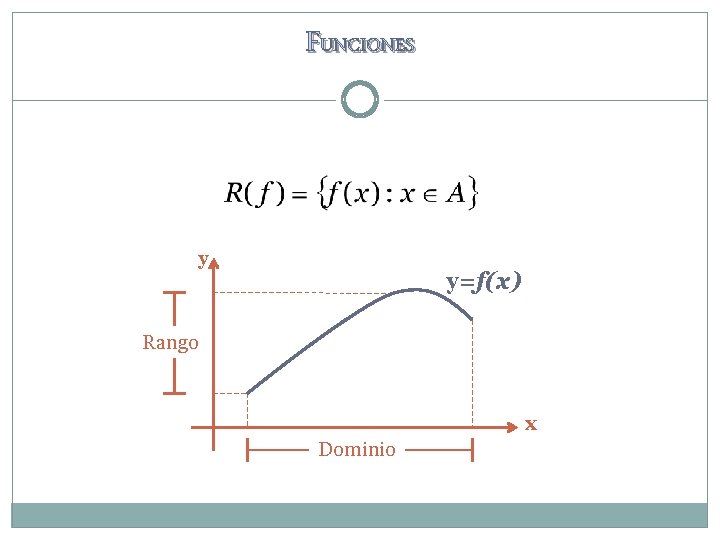
FUNCIONES y y=f(x) Rango x Dominio

FUNCIONES Ejemplo Encuentre el dominio y rango de cada función: 1. f(x)=2 x-1 2. g(x)=x 2

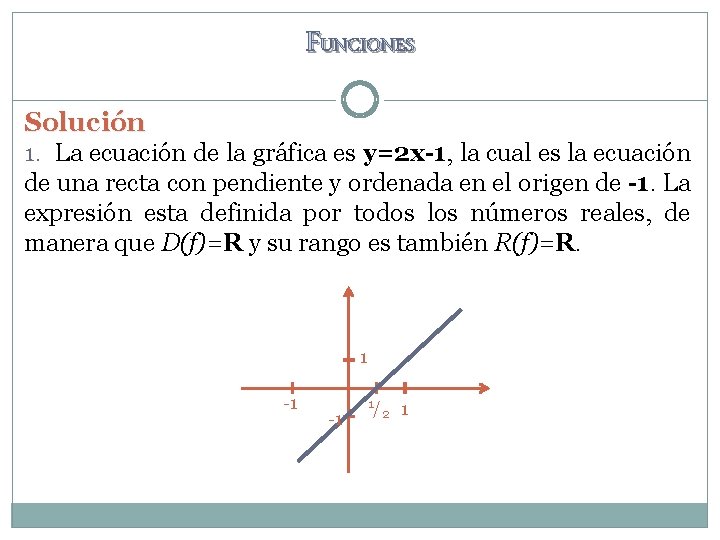
FUNCIONES Solución 1. La ecuación de la gráfica es y=2 x-1, la cual es la ecuación de una recta con pendiente y ordenada en el origen de -1. La expresión esta definida por todos los números reales, de manera que D(f)=R y su rango es también R(f)=R. 1 -1 -1 1/ 2 1

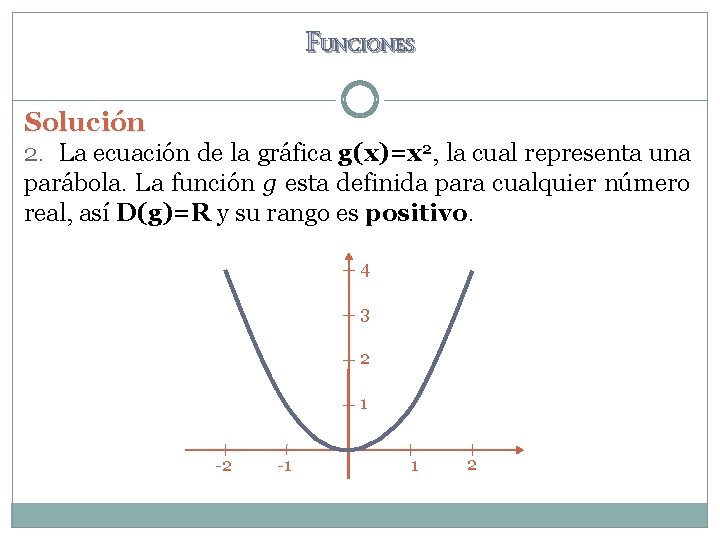
FUNCIONES Solución 2. La ecuación de la gráfica g(x)=x 2, la cual representa una parábola. La función g esta definida para cualquier número real, así D(g)=R y su rango es positivo. 4 3 2 1 -2 -1 1 2

I. 1 EXPONENCIAL Y LOGARÍTMICA Funciones Potencia Funciones donde la base es una variable y la potencia es una constante, tiene la siguiente forma: Ejemplos:

I. 1 EXPONENCIAL Y LOGARÍTMICA Función Exponencial Función donde la base es una constante y la potencia es una variable, es la función exponencial de base a, tiene la siguiente forma: Ejemplos:

I. 1 EXPONENCIAL Y LOGARÍTMICA Propiedades de la Función Exponencial Siendo: 1. 4. 2. 5. 3. 6.

I. 1 EXPONENCIAL Y LOGARÍTMICA En cálculo se decide trabajar como base el número irracional e que tiene un valor aproximado de 2. 71828. Definición La función exponencial para cualquier x є R se define como: Cuenta con las mismas propiedades que cualquier función exponencial de base a.

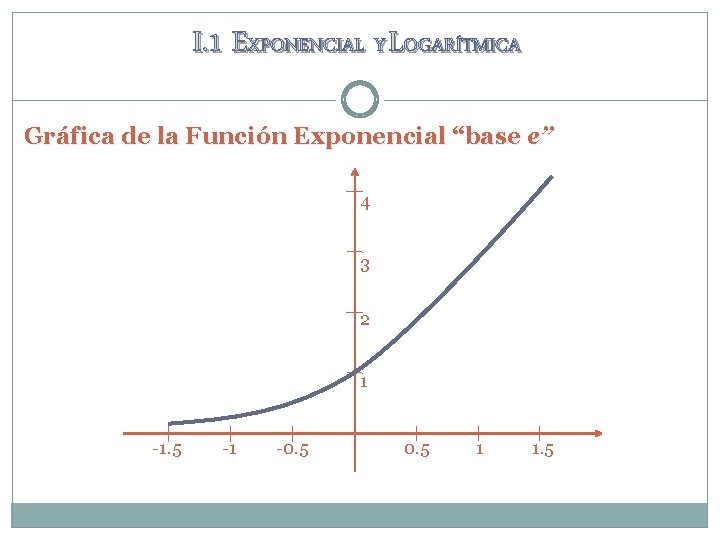
I. 1 EXPONENCIAL Y LOGARÍTMICA Gráfica de la Función Exponencial “base e” 4 3 2 1 -1. 5 -1 -0. 5 1 1. 5

I. 1 EXPONENCIAL Y LOGARÍTMICA Función Logarítmica Para a>0 y a 1 y x>0 denotamos la función logaritmo de base a por logax, y se define como: Si x>0 entonces logax es el exponente al que debe elevarse la base a para dar x.

I. 1 EXPONENCIAL Y LOGARÍTMICA Las funciones exponenciales y logarítmicas son funciones inversas una de otra, como se puede ver en los siguientes ejemplos: Forma Logarítmica Forma Exponencial log 28=3 23=8 loga 1=0 a 0=1 log 10 0. 1=-1 10 -1=0. 1 log 10 1000=3 103=1000

I. 1 EXPONENCIAL Y LOGARÍTMICA Propiedades de la Función Logarítmica Siendo: a, b 1 y x, y >0 se tienen las siguientes características: 1. 2. 3. 4. 5. 6. 7.

I. 1 EXPONENCIAL Y LOGARÍTMICA Logaritmo Natural Es la función para un x>0 se define como la función logaritmo cuya base es el número e y se denota por: Esta función goza de las mismas características que la función logarítmica de base a, dados x, y > 0.

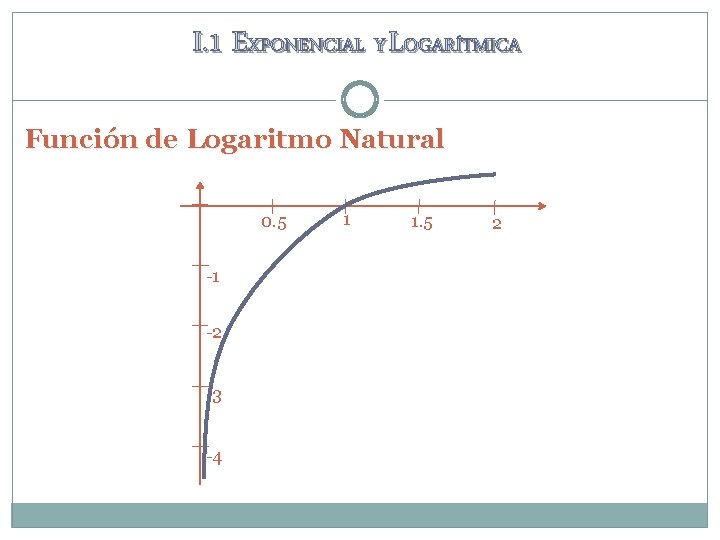
I. 1 EXPONENCIAL Y LOGARÍTMICA Función de Logaritmo Natural 0. 5 -1 -2 -3 -4 1 1. 5 2

I. 1 EXPONENCIAL Y LOGARÍTMICA Propiedades como Funciones Inversas 1. Si a > 0 y a 1 se tiene: 2. Si a = e se tiene:

I. 1 EXPONENCIAL Y LOGARÍTMICA Ejemplo: Desarrolla las siguientes expresiones:

I. 1 EXPONENCIAL Y LOGARÍTMICA Solución: 1. Aplicando la propiedad 4 de logaritmos:

I. 1 EXPONENCIAL Y LOGARÍTMICA Solución: 2. Aplicando la propiedad 5 de logaritmo natural:

I. 1 EXPONENCIAL Y LOGARÍTMICA Solución: 3. Aplicando la propiedad 3 y 4 de logaritmos:

I. 1 EXPONENCIAL Y LOGARÍTMICA Solución: 4. Aplicando la propiedad 3, 4 y 5 de logaritmo natural:

I. 1 EXPONENCIAL Y LOGARÍTMICA Ejercicios para Resolver en Clase: 1. Escribir cada ecuación logarítmica mediante exponencial y viceversa: a) ln 8. 4 = 2. 128 b) 491/2 = 7 2. Desarrolla cada una de las siguientes ecuaciones: a) log 2 x 2 y b) ln(z-1)2

I. 1 EXPONENCIAL Y LOGARÍTMICA Ejercicios de Tarea: 1. Desarrolla la siguiente expresión: 2. Despejar x de las siguientes expresión: a) b) c)

I. 2 DIFERENCIACIÓN DE LAFUNCIÓN EXPONENCIAL Funciones de Base Arbitraria Para a>0 y a 1 y u=u(x) una función diferencial en x donde xєR entonces la derivada de ax es: y para la derivada de au es:

I. 2 DIFERENCIACIÓN DE LAFUNCIÓN EXPONENCIAL Ejemplo: 1. Derivar las siguientes funciones: (a) y=2 x (b) y=2 senx Solución: (a) (b)

I. 2 DIFERENCIACIÓN DE LAFUNCIÓN EXPONENCIAL Funciones de Base e Para a>0 y a 1 y u=u(x) una función diferencial en x donde xєR entonces la derivada de ex es: y para la derivada de eu es:

I. 2 DIFERENCIACIÓN DE LAFUNCIÓN EXPONENCIAL Ejercicios para Realizar en Clase: 1. Calcular las derivadas de las siguientes expresiones: a) y=e 3 x+1 b) y=(ex+1)2 c) y=e 3 x d) y=etan 3 x

I. 2 DIFERENCIACIÓN DE LAFUNCIÓN EXPONENCIAL Ejercicios de Tarea: 1. Calcular las derivadas de las siguientes expresiones: a) y=a 5 x-1 b) y=x 2 ex c) y=e 5 x

I. 3 DIFERENCIACIÓN DE LAFUNCIÓN LOGARÍTMICA Derivación con Base Arbitraria: Si a>0, a 1 y u=u(x), es una función diferenciable de x, donde x>0, entonces la derivada de logax es: y la derivada de logau es:

I. 3 DIFERENCIACIÓN DE LAFUNCIÓN LOGARÍTMICA Ejemplo: 1. Derivar las siguientes funciones: (a) y=log 10 cosx (b) y=log 5(2+senx) Solución: (a) (b)

I. 3 DIFERENCIACIÓN DE LAFUNCIÓN LOGARÍTMICA Derivación con Base e Si a>0, a 1 y u=u(x), es una función diferenciable de x, donde x>0, entonces la derivada de lnx es: y la derivada de lnu es:

I. 3 DIFERENCIACIÓN DE LAFUNCIÓN LOGARÍTMICA Ejemplo: 1. Derivar las siguientes funciones: (a) (b) Solución: (a) (b)

I. 3 DIFERENCIACIÓN DE LAFUNCIÓN LOGARÍTMICA Ejercicios para Resolver en Clase: 1. Derivar las siguientes funciones: a) b) c)

I. 3 DIFERENCIACIÓN DE LAFUNCIÓN LOGARÍTMICA Ejercicios de Tarea: 1. Derivar las siguientes funciones: a) b)

I. 3. 1 DIFERENCIACIÓN LOGARÍTMICA El cálculo de derivadas de funciones complicadas que comprenden productos, cocientes o potencias se puede simplificar tomando logaritmos. Método de la Derivación Logarítmica: 1. Tome logaritmos naturales en ambos miembros de una ecuación y=f(x) y aplique la propiedad de los logaritmos para simplificar. 2. Derive con respecto a x. 3. Resuelva la ecuación resultante para y’.

I. 3. 1 DIFERENCIACIÓN LOGARÍTMICA Ejemplo: 1. Derivar las siguiente ecuación: Solución:

I. 3. 1 DIFERENCIACIÓN LOGARÍTMICA Ejercicios para Resolver en Clases: 1. Aplique la derivación logarítmica para hallar la derivada de las siguientes funciones: a) b)

I. 3. 1 DIFERENCIACIÓN LOGARÍTMICA Ejercicios de Tarea: 1. Aplique la derivación logarítmica para hallar la derivada de las siguientes funciones: a) b)

C APÍTULO II Integrales

II. 1 INTEGRAL INDEFINIDA Definición Una función F se dice que es una primitiva o antiderivada de f en un intervalo I si F’(x)=f(x) para todo x є I. Ejemplo Se necesita encontrar una función F que su derivada sea f(x)=4 x 3, por los conocimientos en diferenciación se diría que: Por lo tanto F es una primitiva de f.

II. 1 INTEGRAL INDEFINIDA Familia de Primitivas: Si F es una primitiva de f en un intervalo I, entonces G es una primitiva de f en I si y solo si G es de la forma: Ejemplo Sabemos que la función F(x)=x 4 es una primitiva de f(x)=4 x 3 así que las siguientes funciones: G 1(x)=x 4+5 G 2(x)=x 4 -123 también son primitivas de f(x). Es la familia de primitivas de f(x)

II. 1 INTEGRAL INDEFINIDA Para denotar la primitiva de una función f se usa la notación: Definición El proceso de calcular las primitivas de una función f se denomina integración, así que tenemos: lo que significa que:

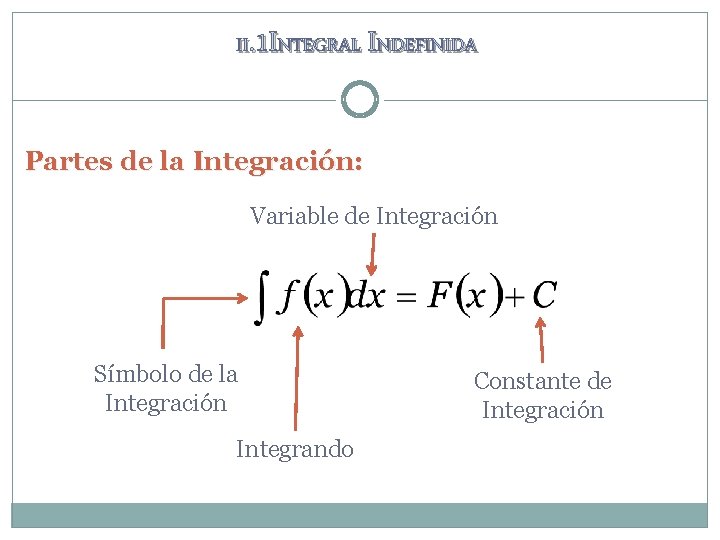
II. 1 INTEGRAL INDEFINIDA Partes de la Integración: Variable de Integración Símbolo de la Integración Integrando Constante de Integración

II. 1 INTEGRAL INDEFINIDA Reglas de la Integración: 1. 2. 3. 4. 5. 6. 7. 8.

II. 1 INTEGRAL INDEFINIDA Reglas de la Integración: 9. 10. 11. 12. 13. 14.

II. 1 INTEGRAL INDEFINIDA Ejemplo: Encuentre las siguientes integrales indefinidas: 1. 2. 3. 4. 5.

II. 1 INTEGRAL INDEFINIDA Solución: 1. 2. 3.

II. 1 INTEGRAL INDEFINIDA Solución: 4. 5.

II. 1 INTEGRAL INDEFINIDA Ejercicios para resolver en Clase: Encuentre las siguientes integrales indefinidas: 1. 2. 3.

II. 1 INTEGRAL INDEFINIDA Ejercicios de Tarea: Encuentre las siguientes integrales indefinidas: 1. 2. 3.

II. 2 INTEGRACIÓN DE FUNCIONES TRIGONOMÉTRICAS Identidades Fundamentales: 1. 2. 3. 4. 5. 6. 7. 8.

II. 2 INTEGRACIÓN DE FUNCIONES TRIGONOMÉTRICAS Con las identidades mencionadas anteriormente se extienden las fórmulas básicas de integración: 15. 16. 17. 18.

II. 2 INTEGRACIÓN DE FUNCIONES TRIGONOMÉTRICAS Ejemplo: Calcular la siguiente integral Solución:

II. 2 INTEGRACIÓN DE FUNCIONES TRIGONOMÉTRICAS Ejercicios para Resolver en Clases: 1. Resolver las siguientes integrales a) b) c)

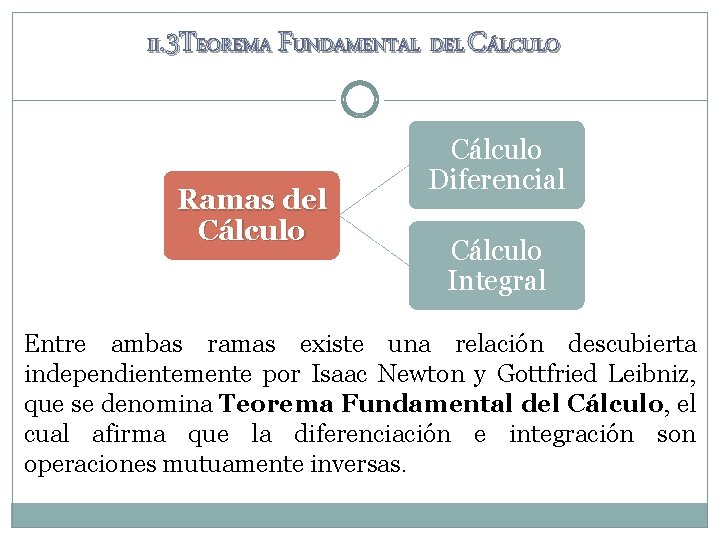
II. 3 TEOREMA FUNDAMENTAL DEL CÁLCULO Ramas del Cálculo Diferencial Cálculo Integral Entre ambas ramas existe una relación descubierta independientemente por Isaac Newton y Gottfried Leibniz, que se denomina Teorema Fundamental del Cálculo, el cual afirma que la diferenciación e integración son operaciones mutuamente inversas.

II. 3 TEOREMA FUNDAMENTAL DEL CÁLCULO Teorema Fundamental de Cálculo Si f(x) es una función continua en [a, b] y F es una primitiva de f en [a, b] entonces: Para aplicarlo se va a utilizar la siguiente notación:

II. 3 TEOREMA FUNDAMENTAL DEL CÁLCULO Propiedades de la Integral Definida Sea f(x) una función integrable en [a, b], entonces: 1. Si k es cualquier constante entonces: 2. Si g(x) es una función integrable en [a, b], entonces:

II. 3 TEOREMA FUNDAMENTAL DEL CÁLCULO Propiedades de la Integral Definida 3. Sea c є [a, b], es decir, a<c<b. Entonces f es integrable en [a, b], si solo si f es integrable en [a, c] y en [c, b]: 4. La integral definida sobre un punto es cero, esto es:

II. 3 TEOREMA FUNDAMENTAL DEL CÁLCULO Propiedades de la Integral Definida 5. La integral definida de a a b de f es igual a menos la integral definida de b a a de f, es decir:

II. 3 TEOREMA FUNDAMENTAL DEL CÁLCULO Ejemplo Resuelva las siguientes integrales: 1. 2.

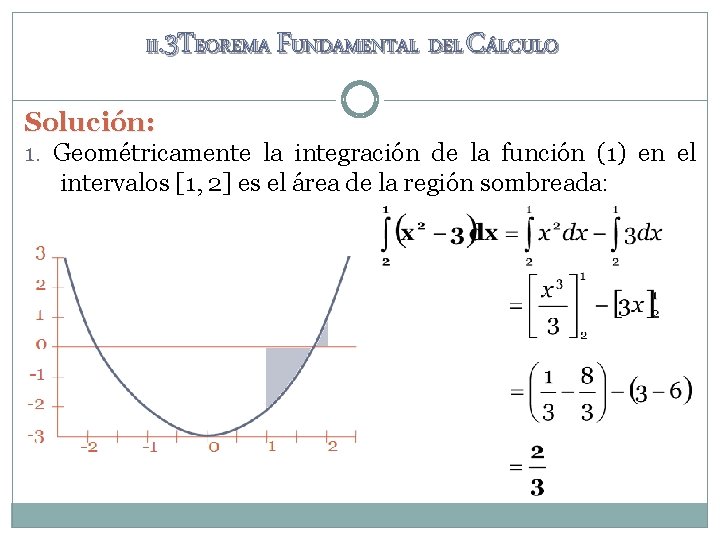
II. 3 TEOREMA FUNDAMENTAL DEL CÁLCULO Solución: 1. Geométricamente la integración de la función (1) en el intervalos [1, 2] es el área de la región sombreada:

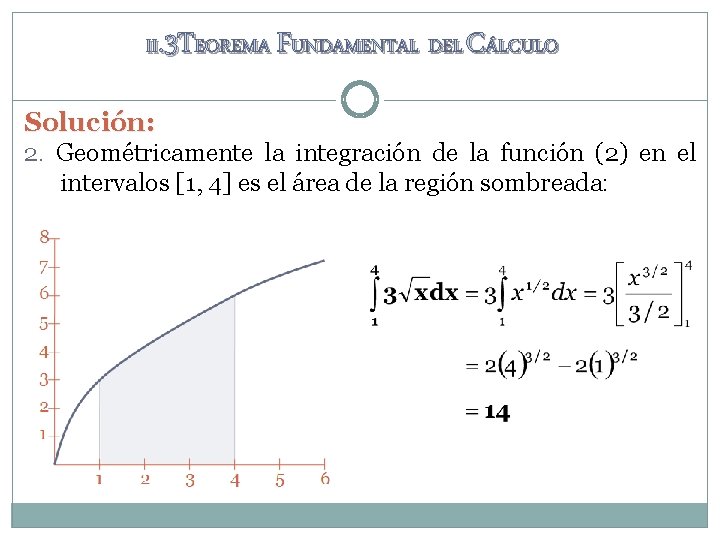
II. 3 TEOREMA FUNDAMENTAL DEL CÁLCULO Solución: 2. Geométricamente la integración de la función (2) en el intervalos [1, 4] es el área de la región sombreada:

II. 3 TEOREMA FUNDAMENTAL DEL CÁLCULO Ejercicios para Resolver en Clase Resolver las siguientes integrales: 1. 2. 3.

II. 3 TEOREMA FUNDAMENTAL DEL CÁLCULO Ejercicios de Tarea Resolver las siguientes integrales: 1. 2. 3.

II. 4 MÉTODO DE SUSTITUCIÓN Método de Sustitución Sea g una función cuyo rango es un intervalo I, y sea f una función continua en I. Si g es diferenciable en su dominio y F es una primitiva de f en I, entonces: Si hacemos el cambio de variable u=g(x) entonces du=g’(x)dx y: Este método es comparable a la regla de la cadena en la diferenciación.

II. 4 MÉTODO DE SUSTITUCIÓN Ejemplo: 1. Resolver la integral: Solución:

II. 4 MÉTODO DE SUSTITUCIÓN Ejercicios para Resolver en Clases 1. Resuelva las siguientes ecuaciones: a) b) c)

II. 4. 1 SUSTITUCIÓN PARA INTEGRALES DEFINIDAS Existen dos métodos para evaluar una integral definida por sustitución. Uno de ellos es evaluar primero la integral indefinida y en seguida aplicar el TFC, por ejemplo:

II. 4. 1 SUSTITUCIÓN PARA INTEGRALES DEFINIDAS El otro método suele ser el mas adecuado, en este se cambian los límites de integración cuando se cambie la variable, como se explica a continuación: Si g’ es continua sobre el intervalo [a, b] y f lo es sobre el rango de u=g(x) entonces

II. 4. 1 SUSTITUCIÓN PARA INTEGRALES DEFINIDAS Ejemplo Solución Tomando la sustitución u=2 x+1 tenemos que Hallamos los nuevos límites de integración:

II. 4. 1 SUSTITUCIÓN PARA INTEGRALES DEFINIDAS Por lo tanto:

II. 4. 1 SUSTITUCIÓN PARA INTEGRALES DEFINIDAS Ejemplo: Evaluar la siguiente integral

II. 4. 1 SUSTITUCIÓN PARA INTEGRALES DEFINIDAS Ejercicios para Resolver en Clase Evaluar las siguientes integrales: 1. 2. 3.

II. 4 MÉTODO DE SUSTITUCIÓN Ejercicios de Tarea Calcular las siguientes integrales 1. 2. 3.

II. 5 INTEGRACIÓN POR PARTES Sea f y g funciones diferenciables en un intervalo I, entonces: Se puede utilizar otra notación, que es más fácil de recordar, la cual se muestra a continuación:

II. 5 INTEGRACIÓN POR PARTES Ejemplo Solución De manera que:

II. 5 INTEGRACIÓN POR PARTES Solución Notamos que si hubiéramos elegido u=senx y dv=xdx, entonces du=cosx y v=x 2/2 por lo que: es una integral mas difícil de calcular.

II. 5 INTEGRACIÓN POR PARTES Ejemplo Solución De manera que: La integral obtenida es mas sencilla que la inicial pero aun no es obvia, por lo cual hay que volver a aplicar la integración por partes.

II. 5 INTEGRACIÓN POR PARTES Sustituyendo el resultado de la segunda ecuación tenemos que:

II. 5 INTEGRACIÓN POR PARTES Ejercicios para Resolver en Clase Resuelva las siguientes integrales: 1. 2. 3. 4.

II. 5 INTEGRACIÓN POR PARTES Fórmula de Integración por Partes para Integrales Definidas

II. 5 INTEGRACIÓN POR PARTES Ejemplo De donde: Por lo tanto:

II. 5 INTEGRACIÓN POR PARTES Ejercicios de Tarea Resuelva las siguientes integrales: 1. 5. 2. 6. 3. 7. 4.

C APÍTULO III Ecuaciones Diferenciales

III. 1 INTRODUCCIÓN Definición Una ecuación diferencial (ED) es una ecuación que involucra derivadas de una función desconocida de una o varias variables. Ejemplo Las siguientes expresiones son ejemplos de ED’s: Conocida como Ley de Crecimiento Exponencial

III. 1 INTRODUCCIÓN En basa a la definición anterior se tiene que: a) Si la función desconocida depende de solo una variable la ecuación se llama Ecuación Diferencial Ordinaria. b) Si la función desconocida depende de más de una variable la ecuación se llama Ecuación Diferencial Parcial.

III. 1 INTRODUCCIÓN Las ecuaciones diferenciales pueden clasificarse por su orden y grado. Orden El orden de una ecuación diferencial es el orden de la derivada mas alta que aparece en la ecuación. Ejemplo Determinar el orden de las ecuaciones diferenciales:

III. 1 INTRODUCCIÓN Solución La ecuación diferencial: Es de primer orden dado que la derivada mas alta que figura en la ecuación diferencial es la primera derivada. La ecuación diferencial: Es de segundo orden dado que la derivada más alta que figura en la ecuación diferencial es la de la segunda derivada.

III. 1 INTRODUCCIÓN Ejercicios para resolver en clase Determinar el orden de las siguientes ecuaciones: a) b)

III. 1 INTRODUCCIÓN Grado El grado de una ecuación diferencial es el grado algebraico de su derivada de mayor orden, es decir, el grado de una ecuación diferencial es la potencia a la que esta elevada la deriva que nos dio el orden de la ecuación diferencial. Ejemplo El grado de la ecuación diferencial es: de tercer grado, dado que la primera derivada está elevada cubo.

III. 1 INTRODUCCIÓN Ejercicios para resolver en clase Determinar el grado de las siguientes ecuaciones: a) b)

III. 1 INTRODUCCIÓN NOTA: cuando alguna derivada este dentro de un radical o en polinomio, el cual este elevado a una potencia fraccionaria, tendremos que eliminar dicho radical para después determinar el grado de la ecuación diferencial.

III. 1 INTRODUCCIÓN Ejercicios para resolver en clases Determinar el orden y grado de las siguientes ecuaciones diferenciales: a) b)

III. 1 INTRODUCCIÓN Ejercicios para resolver en clases Determinar el orden y grado de las siguientes ecuaciones diferenciales: a) b)

III. 1 INTRODUCCIÓN Ejercicios de Tarea Determinar el orden y grado de las siguientes ecuaciones diferenciales: a) c) d) b)

III. 2 SOLUCIÓN DE UNAED Una solución de una ED es cualquier función que satisface la ED, este es, la reduce a una identidad. Ejemplo La funciónuna solución es definida la de por ecuación diferencial: puesto que: y al sustituir en la ED se obtiene una identidad

III. 2 SOLUCIÓN DE UNAED Una solución particular de una ED es toda solución obtenida asignando valores específicos a las constantes que intervienen en la solución general. Ejemplo Verificar que y=Cx 3 es solución de la ecuación diferencial Hallar la solución particular sujeta a la condición inicial:

III. 2 SOLUCIÓN DE UNAED Solución Derivando y=Cx 3 tenemos que y’=3 Cx 2, luego, sustituyendo en la ED: de esta manera y=Cx 3 es solución de la ED. Para obtener la solución particular, apliquemos la condición inicial y(-3)=2 en la solución general esto es: La solución particular es:

III. 2. 1 COMPROBACIÓN DE LASOLUCIÓN DE UNAED Para comprobar que una ecuación es o no la solución de una ecuación dada, se aplica el siguiente método: Método 1. Observemos que derivada o derivadas aparecen en la ecuación diferencial. 2. Estas derivas las encontramos al derivar la ecuación que se supone solución. 3. La ecuación será solución cuando al sustituir el valor de las derivadas encontradas (paso 2) dentro de la ecuación diferencial, aparezca una identidad a=a (donde aєR) al reducir la ecuación ya sustituida.

III. 2. 1 COMPROBACIÓN DE LASOLUCIÓN DE UNAED Ejemplo Comprobar que la y=x 2+C no es solución de la ecuación diferencial Solución 1. Observando la ecuación diferencial vemos que aparece una derivada por lo tanto, encontramos su valor derivando la supuesta solución. 2. Derivando y=x 2+C tenemos

III. 2. 1 COMPROBACIÓN DE LASOLUCIÓN DE UNAED Solución 3. Sustituyendo el valor de la derivada encontrada en la ecuación diferencial tenemos: Por lo tanto y=x 2+C si es solución de la ecuación diferencial

III. 2. 1 COMPROBACIÓN DE LASOLUCIÓN DE UNAED Ejercicios para resolver en clase Determine si cada ecuación es solución o no de la ecuación diferencial dada: 1. 2. 3.

III. 2. 1 COMPROBACIÓN DE LASOLUCIÓN DE UNAED Ejercicios de tarea Determine si cada ecuación es solución o no de la ecuación diferencial dada: 1. 2. 3.

III. 3 OBTENCIÓN DE LAED A PARTIR DE LA SOLUCIÓN GENERAL Para obtener la ED a partir de su solución general, aplicaremos el siguiente método: 1. Observemos el número de constantes de integración que aparecen en la solución general dada. 2. Derivemos la solución general tantas veces como el número de constantes de integración aparezcan en ella. En otras palabra, si la solución general tienen n constantes de integración diferentes, entonces derivaremos n veces tal solución.

III. 3 OBTENCIÓN DE LAED A PARTIR DE LA SOLUCIÓN GENERAL 3. Tomando en cuenta el resultado de la última derivada obtenida, se nos pueden presentar los siguientes casos: a) Si en la última derivada ya no aparecen constantes de integración, esta será la ED que de la solución general dada. b) Si la última derivada contiene constantes de integración, habrá que eliminarlas, pudiendo utilizar para esto, las ecuaciones de las derivadas encontradas, asó como también la solución general dada. En la ED NO deben aparecer constantes de integración.

III. 3 OBTENCIÓN DE LAED A PARTIR DE LA SOLUCIÓN GENERAL Ejemplo Encuentre la ED cuya solución general es y=x 2+C Solución Observemos que sólo aparece una constante de integración, de manera que derivamos una sola vez la solución general y=x 2+C. Así Como en esta derivada no aparecen constantes de integración, quiere decir que esta es la ED de la solución general presentada al inicio.

III. 3 OBTENCIÓN DE LAED A PARTIR DE LA SOLUCIÓN GENERAL Ejemplo Encuentre la ED cuya solución general es y=Cx 2 Solución Observemos que sólo aparece una constante de integración, de manera que derivamos una sola vez la solución general y=Cx 2. Así Se va a despejar C de la solución general y se sustituye el valor encontrado en la ED.

III. 3 OBTENCIÓN DE LAED A PARTIR DE LA SOLUCIÓN GENERAL Solución Por lo tanto: Es la ED de la solución general puesto que ya no aparecen constantes de integración.

III. 3 OBTENCIÓN DE LAED A PARTIR DE LA SOLUCIÓN GENERAL Ejercicios para resolver en clase Encuentre la ED de las siguientes soluciones generales 1. 2.

III. 3 OBTENCIÓN DE LAED A PARTIR DE LA SOLUCIÓN GENERAL Ejercicios de tarea Encuentre la ED de las siguientes soluciones generales 1. 2.