MATEMTICA FINANCIERA Los ejercicios de esta presentacin son

MATEMÁTICA FINANCIERA

Los ejercicios de esta presentación son tomados de: RAMÍREZ MOLINARES, C. , GARCIA BARBOSA, M. , PANTOJA ALGARIN, C. , ZAMBRANO MEZA, A. Fundamentos de Matemáticas Financieras. Universidad Libre de Cartagena, Colombia. 2009. Recuperado de http: //www. uv. mx/personal/cbustamante/files/2011/06/MATEMATI CAS_FINANCIERAS. pdf

ANUALIDADES Docente Mag. Carlos Alberto Muñoz Gutiérrez

ANUALIDADES Tiempo Períodos de Cap. o pagos ANUALIDAD Momento en que se realiza el pago de la renta Período en que se realiza el primer pago Fórmulas Matemática Financiera

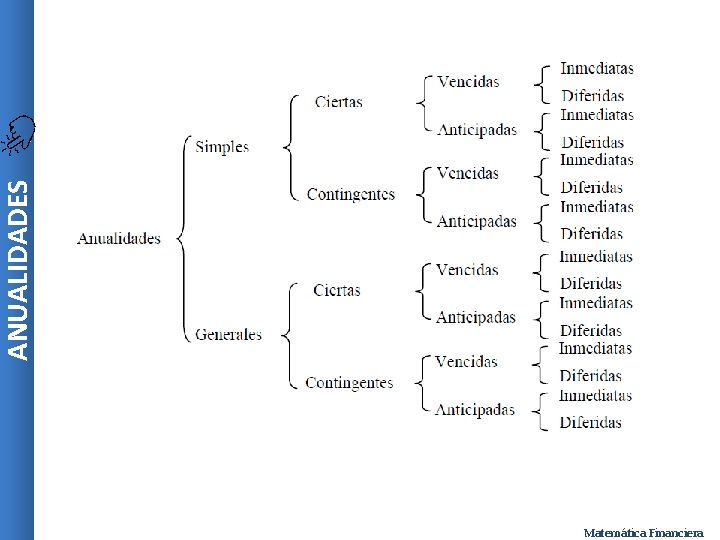
ANUALIDADES CIERTAS Si se conocen las fechas de inicio y terminación de la anualidad. TIEMPO ANUALIDADES EVENTUALES o CONTINGENTES Si una de las dos fechas de inicio o terminación se desconocen. Matemática Financiera

ANUALIDADES SIMPLES Períodos de Capitalización o pagos Si el periodo de capitalización y el de pago son iguales. ANUALIDADES GENERALES Si los periodos de pago capitalización son diferentes. y de Matemática Financiera

ANUALIDADES ANUALIDAD ORDINARIA Momento en que se realiza el pago de la renta Si el pago de la renta se realiza al final de cada periodo. Se le llama también ANUALIDAD VENCIDA. ANUALIDADES GENERALES: ANUALIDAD ANTICIPADA Se llama así porque los pagos se realizan al principio de cada periodo. Matemática Financiera

ANUALIDADES ANUALIDAD INMEDIATA Período en que se realiza el primer pago Si el primer pago de la renta se realiza en el primer periodo. ANUALIDADES GENERALES: ANUALIDAD DIFERIDA: Si el primer pago de la renta se realiza varios periodos después del inicio. Matemática Financiera

ANUALIDADES Matemática Financiera

Fórmulas Dar Click sobre cada formula para ver ejemplo Anualidad Vencidas Futuro Presente Anticipadas Futuro Presente ANUALIDADES Presente/Futuro Tiempo Matemática Financiera

Vencidas Presente ANUALIDADES Ejemplo 1 Una persona adquiere a crédito un electrodoméstico que cancelará en 12 pagos mensuales iguales de $ 300. 000, a una tasa de 2% mensual. Encontrar el valor de contado del electrodoméstico. Fórmulas Ver Ejemplo 2 Matemática Financiera

Vencidas Presente ANUALIDADES Ejemplo 2 Una persona adquiere un vehículo a crédito con una cuota inicial de $ 5. 000 y 24 cuotas mensuales iguales de $ 580. 000. El concesionario le cobra un 2, 3% mensual sobre saldo. Encontrar el valor del vehículo. Fórmulas Matemática Financiera

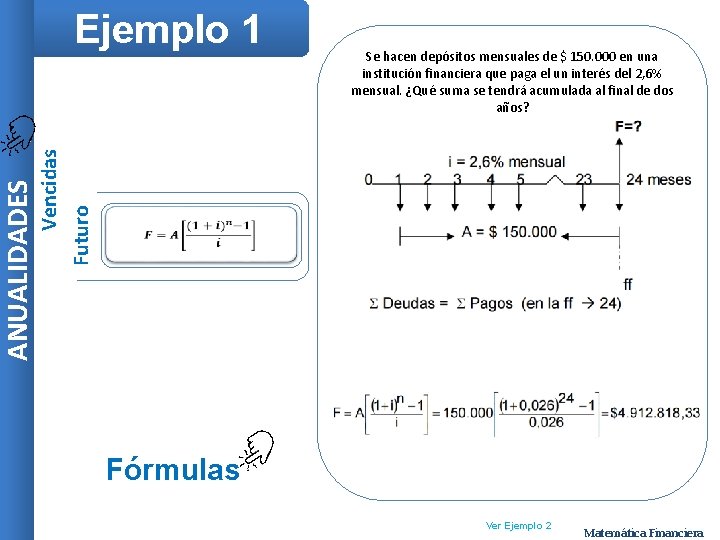
Vencidas Futuro ANUALIDADES Ejemplo 1 Se hacen depósitos mensuales de $ 150. 000 en una institución financiera que paga el un interés del 2, 6% mensual. ¿Qué suma se tendrá acumulada al final de dos años? Fórmulas Ver Ejemplo 2 Matemática Financiera

Vencidas Futuro ANUALIDADES Ejemplo 2 Una persona deposita hoy en una institución financiera la suma de $ 820. 000 que le paga una tasa de interés del 3% mensual. Calcular el valor acumulado al final de año, si cada mes deposita $ 300. 000? Fórmulas Matemática Financiera

Anualidad Vencidas Presente ANUALIDADES Ejemplo 1 Un apartamento se adquiere a crédito por la suma de $ 60. 000 en cuota mensuales iguales, la obligación se pacta a 15 años a una tasa de interés del 3% mensual. Determinar el valor de las cuotas. Fórmulas Ver Ejemplo 2 Matemática Financiera

Anualidad Vencidas Presente ANUALIDADES Ejemplo 2 Un empresa desea construir una fábrica, por lo cual adquiere un terreno por la suma de $ 30. 000 dando una cuota inicial del 15% y 24 cuota mensuales con una tasa de interés del 2. 5%. Calcular el valor de las cuotas. Fórmulas Matemática Financiera

Anualidad Vencidas Futuro ANUALIDADES Ejemplo 1 Una empresa necesitará reponer una máquina dentro de 6 años, la cual, en ese momento tendrá un valor de mercado de $ 1. 800. 000. De acuerdo a estudios de mercado realizados, se espera que la máquina cueste alrededor de $ 9, 500. 000 y se decide hacer un fondo para cubrir el costo. Si se puede obtener una tasa de interés del 30% ACS, ¿Cuánto se tiene que depositar cada semestre para tener el dinero para reponer la máquina al final de su vida útil? Fórmulas Ver Ejemplo 2 Matemática Financiera

Anualidad Vencidas Futuro ANUALIDADES Ejemplo 2 El gerente de un hospital desea invertir en una institución financiera para comprar un equipo de Rx en un término de dos años. Para esto debe destinar cierta cantidad cada bimestre hasta completar la cantidad $ 100. 000. Si la institución financiera reconoce un 24% AC Bimestralmente, determínese el valor del depósito bimestral. Fórmulas Matemática Financiera

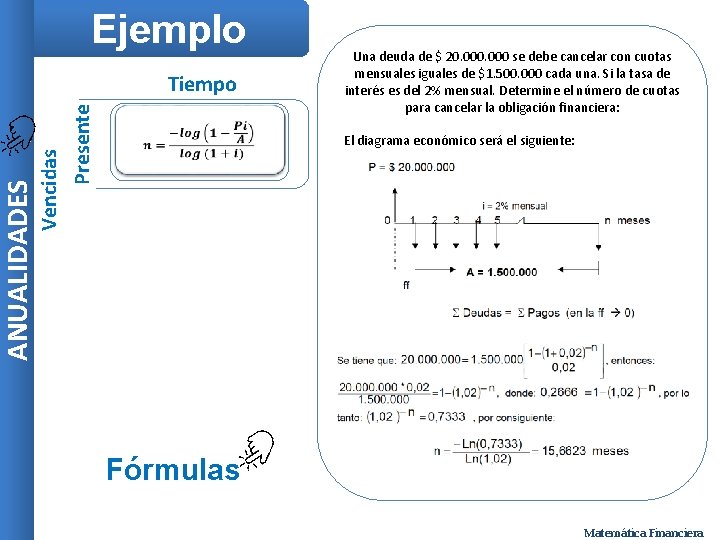
Tiempo Vencidas Presente ANUALIDADES Ejemplo Una deuda de $ 20. 000 se debe cancelar con cuotas mensuales iguales de $1. 500. 000 cada una. Si la tasa de interés es del 2% mensual. Determine el número de cuotas para cancelar la obligación financiera: El diagrama económico será el siguiente: Fórmulas Matemática Financiera

Tiempo Vencidas Futuro ANUALIDADES Ejemplo Se desea tener un monto de $ 17. 450. 260 mediante depósitos cada dos meses vencidos de $ 430. 230. Calcular cuántos depósitos se deben hacer si se ganan intereses del 18% Capitalizable cada bimestre. Fórmulas Matemática Financiera

Ejemplo 1 Anticipadas Presente ANUALIDADES Fórmulas Supóngase el caso de un contrato de arrendamiento por un año, en el que los pagos del canon son mensuales por un valor de $700. 000, si las partes del contrato acuerdan que se realice un solo pago al principio del contrato y la tasa estipulada es del 3% mensual, de cuanto sería el valor de ese pago único. Ver Ejemplo 2 Matemática Financiera

Ejemplo 2 Se ha pactado una obligación para cancelar en 24 cuotas iguales de $ 125. 000 cada una por mes anticipado, si se decide cancelarla de contado a un interés del 2, 5% mensual, cuál es el valor. Anticipadas Presente ANUALIDADES Fórmulas Matemática Financiera

Ejemplo 2 Se ha pactado una obligación para cancelar en 24 cuotas iguales de $ 125. 000 cada una por mes anticipado, si se decide cancelarla de contado a un interés del 2, 5% mensual, cuál es el valor. Anticipadas Presente ANUALIDADES Fórmulas Matemática Financiera

Ejemplo 1 Anticipadas Futuro ANUALIDADES Fórmulas Una persona recibe por concepto de arriendo (mes anticipado), la suma de $1. 000 mensuales, y deposita el 30% en una cuenta de ahorros en una institución financiera, que le reconoce el 2% de interés mensual. El depósito lo realiza un vez recibe el valor de la renta. Si el in mueble estuvo arrendado por un año, ¿Cuanto tendrá acumulado en la cuenta al final de los 12 meses? Ver Ejemplo 2 Matemática Financiera

Ejemplo 2 Una persona deposita $ 800. 000, al principio de cada mes, en un fondo que reconoce el 2% mensual. Después de 2, 5 años no hizo más depósito, pero dejó el dinero acumulado hasta ese momento, 1, 5 año más a la misma tasa de interés. Calcular el valor acumulado. Anticipadas Futuro ANUALIDADES Fórmulas Matemática Financiera

Ejemplo Anualidad Se recibe un préstamo de $ 15. 000 para cancelarlo en 15 cuotas mensuales iguales, pagaderas en forma anticipada, si la tasa de interés es del 3, 5% mensual, hallar el valor de las cuotas. Anticipadas Presente ANUALIDADES Fórmulas Matemática Financiera

Ejemplo Anualidad Anticipadas Futuro ANUALIDADES Fórmulas Una persona recibe por concepto de arriendo (mes anticipado), la suma de $1. 000 mensuales, y deposita el 30% en una cuenta de ahorros en una institución financiera, que le reconoce el 2% de interés mensual. El depósito lo realiza un vez recibe el valor de la renta. Si el in mueble estuvo arrendado por un año, ¿Cuanto tendrá acumulado en la cuenta al final de los 12 meses? Matemática Financiera

Ejemplo Tiempo Una obligación de $ 5. 000 se va a cancelar con pagos mensuales iguales anticipados de 580. 185, 46. Si la tasa de interés es del 2, 8% mensual, calcular el número de pagos que garanticen el pago de la obligación. Anticipadas Presente ANUALIDADES Fórmulas Matemática Financiera

Ejemplo Tiempo Un empleado consigna $ 400. 000 al principio de cada mes en una cuenta de ahorros que paga el 28%, convertible mensualmente. ¿En cuánto tiempo logrará ahorrar $30. 000? Anticipadas Futuro ANUALIDADES Fórmulas Matemática Financiera

ANUALIDADES ANUALIDAD Se refiere a un conjunto de pagos, depósitos o retiros por la misma cantidad realizados a intervalos iguales de tiempo. EJEMPLOS: ü Sueldos ü Pagos de pensiones ü Intereses de inversiones ü Alquileres de edificios ü Pagos en abonos ü Primas de seguros. Matemática Financiera